Additional Tools: Difference between revisions

From ReliaWiki
Jump to navigation Jump to search
No edit summary
 
(17 intermediate revisions by 2 users not shown)
Line 1: Line 1:
{{template:ALTABOOK|11}}
{{template:ALTABOOK|11}}
=Common Shape Parameter Likelihood Ratio Test=
==Common Shape Parameter Likelihood Ratio Test==
In order to assess the assumption of a common shape parameter among the data obtained at various stress levels, the likelihood ratio (LR) test can be utilized, as described in Nelson [[Appendix_E:_References|[28]]]. This test applies to any distribution with a shape parameter. In the case of ALTA, it applies to the Weibull and lognormal distributions. When Weibull is used as the underlying life distribution, the shape parameter, <math>\beta ,\,\!</math> is assumed to be constant across the different stress levels (i.e., stress independent). Similarly, <math>{{\sigma }_{{{T}'}}}\,\!</math>, the parameter of the lognormal distribution is assumed to be constant across the different stress levels.


In order to assess the assumption of a common shape parameter among the data obtained at various stress levels, the likelihood ratio (LR) test can be utilized [[Reference Appendix D: References|[28]]]. This test applies to any distribution with a shape parameter. In the case of ALTA, it applies to the Weibull and lognormal distributions. When Weibull is used as the underlying life distribution, the shape parameter,  <math>\beta ,</math>  is assumed to be constant across the different stress levels (i.e., stress independent). Similarly, <math>{{\sigma }_{{{T}'}}}</math>, the parameter    of the lognormal distribution is assumed to be constant across the different stress levels.
The likelihood ratio test is performed by first obtaining the LR test statistic, <math>T\,\!</math>. If the true shape parameters are equal, then the distribution of <math>T\,\!</math> is approximately chi-square with <math>n-1\,\!</math> degrees of freedom, where <math>n\,\!</math> is the number of test stress levels with two or more exact failure points. The LR test statistic, <math>T\,\!</math>, is calculated as follows:
The likelihood ratio test is performed by first obtaining the LR test statistic, <math>T</math>. If the true shape parameters are equal, then the distribution of <math>T</math> is approximately chi-square with <math>n-1</math> degrees of freedom, where <math>n</math> is the number of test stress levels with two or more exact failure points. The LR test statistic, <math>T</math> , is calculated as follows:


::<math>T=2({{\hat{\Lambda }}_{1}}+...+{{\hat{\Lambda }}_{n}}-{{\hat{\Lambda }}_{0}})</math>
::<math>T=2({{\hat{\Lambda }}_{1}}+...+{{\hat{\Lambda }}_{n}}-{{\hat{\Lambda }}_{0}})\,\!</math>


<math>\hat{\Lambda}_{1}, ..., \hat{\Lambda}_{n}</math> are the likelihood values obtained by fitting a separate distribution to the data from each of the <math>n</math> test stress levels (with two or more exact failure times). The likelihood value, <math>{{\hat{\Lambda }}_{0}},</math> is obtained by fitting a model with a common shape parameter and a separate scale parameter for each of the <math>n</math> stress levels, using indicator variables.
where <math>\hat{\Lambda}_{1}, ..., \hat{\Lambda}_{n}\,\!</math> are the likelihood values obtained by fitting a separate distribution to the data from each of the <math>n\,\!</math> test stress levels (with two or more exact failure times). The likelihood value, <math>{{\hat{\Lambda }}_{0}},\,\!</math> is obtained by fitting a model with a common shape parameter and a separate scale parameter for each of the <math>n\,\!</math> stress levels, using indicator variables.


Once the LR statistic has been calculated, then:
Once the LR statistic has been calculated, then:


*If <math>T\le {{\chi }^{2}}(1-\alpha ;n-1),</math> the <math>n</math> shape parameter estimates do not differ statistically significantly at the 100 <math>\alpha %</math> level.
*If <math>T\le {{\chi }^{2}}(1-\alpha ;n-1),\,\!</math> the <math>n\,\!</math> shape parameter estimates do not differ statistically significantly at the 100 <math>\alpha %\,\!</math> level.


*If <math>T>{{\chi }^{2}}(1-\alpha ;n-1),</math> the <math>n</math> shape parameter estimates differ statistically significantly at the 100 <math>\alpha %</math> level.
*If <math>T>{{\chi }^{2}}(1-\alpha ;n-1),\,\!</math> the <math>n\,\!</math> shape parameter estimates differ statistically significantly at the 100 <math>\alpha %\,\!</math> level.


<math>{{\chi }^{2}}(1-\alpha ;n-1)</math> is the 100(1- <math>\alpha )</math> percentile of the chi-square distribution with <math>n-1</math> degrees of freedom.
 
<math>{{\chi }^{2}}(1-\alpha ;n-1)\,\!</math> is the 100(1- <math>\alpha)\,\!</math> percentile of the chi-square distribution with <math>n-1\,\!</math> degrees of freedom.




Line 21: Line 22:
{{:Likelihood Ratio Test Example}}
{{:Likelihood Ratio Test Example}}


 
==Tests of Comparison==
=Tests of Comparison=
 
It is often desirable to be able to compare two sets of accelerated life data in order to determine which of the data sets has a more favorable life distribution. The units from which the data are obtained could either be from two alternate designs, alternate manufacturers or alternate lots or assembly lines. Many methods are available in statistical literature for doing this when the units come from a complete sample, (i.e., a sample with no censoring). This process becomes a little more difficult when dealing with data sets that have censoring, or when trying to compare two data sets that have different distributions. In general, the problem boils down to that of being able to determine any statistically significant difference between the two samples of potentially censored data from two possibly different populations. This section discusses some of the methods that are applicable to censored data, and are available in ALTA.
It is often desirable to be able to compare two sets of accelerated life data in order to determine which of the data sets has a more favorable life distribution. The units from which the data are obtained could either be from two alternate designs, alternate manufacturers or alternate lots or assembly lines. Many methods are available in statistical literature for doing this when the units come from a complete sample, (i.e., a sample with no censoring). This process becomes a little more difficult when dealing with data sets that have censoring, or when trying to compare two data sets that have different distributions. In general, the problem boils down to that of being able to determine any statistically significant difference between the two samples of potentially censored data from two possibly different populations. This section discusses some of the methods that are applicable to censored data, and are available in ALTA.


==Simple Plotting==
===Simple Plotting===
 
One popular graphical method for making this determination involves plotting the data at a given stress level with confidence bounds and seeing whether the bounds overlap or separate at the point of interest.  This can be effective for comparisons at a given point in time or a given reliability level, but it is difficult to assess the overall behavior of the two distributions, as the confidence bounds may overlap at some points and be far apart at others. This can be easily done using the overlay plot feature in ALTA.
One popular graphical method for making this determination involves plotting the data at a given stress level with confidence bounds and seeing whether the bounds overlap or separate at the point of interest.  This can be effective for comparisons at a given point in time or a given reliability level, but it is difficult to assess the overall behavior of the two distributions, as the confidence bounds may overlap at some points and be far apart at others. This can be easily done using the multiple plot feature in ALTA.
 
==Estimating  <math>P\left[ {{t}_{2}}\ge {{t}_{1}} \right]</math>  Using the Comparison Wizard==


===Using the Life Comparison Wizard===
Another methodology, suggested by Gerald G. Brown and Herbert C. Rutemiller, is to estimate the probability of whether the times-to-failure of one population are better or worse than the times-to-failure of the second. The equation used to estimate this probability is given by:
Another methodology, suggested by Gerald G. Brown and Herbert C. Rutemiller, is to estimate the probability of whether the times-to-failure of one population are better or worse than the times-to-failure of the second. The equation used to estimate this probability is given by:


::<math>P\left[ {{t}_{2}}\ge {{t}_{1}} \right]=\int_{0}^{\infty }{{f}_{1}}(t)\cdot {{R}_{2}}(t)\cdot dt</math>
::<math>P\left[ {{t}_{2}}\ge {{t}_{1}} \right]=\int_{0}^{\infty }{{f}_{1}}(t)\cdot {{R}_{2}}(t)\cdot dt\,\!</math>
 
where  <math>{{f}_{1}}(t)</math>  is the  <math>pdf</math>  of the first distribution and  <math>{{R}_{2}}(t)</math>  is the reliability function of the second distribution. The evaluation of the superior data set is based on whether this probability is smaller or greater than 0.50. If the probability is equal to 0.50, that is equivalent to saying that the two distributions are identical.


If given two alternate designs with life test data, where X and Y represent the life test data from two different populations, and if we simply wanted to choose the component at time  <math>t</math> with the higher reliability, one choice would be to select the component with the higher reliability at time  <math>t</math> . However, if we wanted to design a product as long-lived as possible, we would want to calculate the probability that the entire distribution of one product is better than the other and choose X or Y when this probability is above or below 0.50 respectively.
where <math>{{f}_{1}}(t)\,\!</math> is the ''pdf'' of the first distribution and <math>{{R}_{2}}(t)\,\!</math> is the reliability function of the second distribution. The evaluation of the superior data set is based on whether this probability is smaller or greater than 0.50. If the probability is equal to 0.50, then is equivalent to saying that the two distributions are identical.


The statement "the probability that X is greater than or equal to Y" can be interpreted as follows:
For example, consider two alternate designs, where X and Y represent the life test data from each design. If we simply wanted to choose the component with the higher reliability, we could simply select the component with the higher reliability at time <math>t\,\!</math>. However, if we wanted to design the product to be as long-lived as possible, we would want to calculate the probability that the entire distribution of one design is better than the other. The statement "the probability that X is greater than or equal to Y" can be interpreted as follows:


*If <math>P=0.50</math> , then the statement is equivalent to saying that both X and Y are equal.
*If <math>P=0.50\,\!</math>, then the statement is equivalent to saying that both X and Y are equal.


*If <math>P<0.50</math> or, for example, <math>P=0.10</math> , then the statement is equivalent to saying that <math>P=1-0.10=0.90</math> , or Y is better than X with a 90% probability.  
*If <math>P<0.50\,\!</math> or, for example, <math>P=0.10\,\!</math>, then the statement is equivalent to saying that <math>P=1-0.10=0.90\,\!</math>, or Y is better than X with a 90% probability.  


ALTA's Comparison Wizard allows you to perform such calculations. The comparison is performed at the given use stress levels of each data set, using the equation:
ALTA's Comparison Wizard allows you to perform such calculations. The comparison is performed at the given use stress levels of each data set, using the equation:


::<math>P\left[ {{t}_{2}}\ge {{t}_{1}} \right]=\int_{0}^{\infty }{{f}_{1}}(t,{{V}_{Use,1}})\cdot {{R}_{2}}(t,{{V}_{Use,2}})\cdot dt</math>
::<math>P\left[ {{t}_{2}}\ge {{t}_{1}} \right]=\int_{0}^{\infty }{{f}_{1}}(t,{{V}_{Use,1}})\cdot {{R}_{2}}(t,{{V}_{Use,2}})\cdot dt\,\!</math>
 
The disadvantage of this method is that the sample sizes are not taken into account, thus one should avoid using this method of comparison when the sample sizes are different.
 
=Degradation Analysis=


==Degradation Analysis==
Given that products are frequently being designed with higher reliabilities and developed in shorter amounts of time, even accelerated life testing is often not sufficient to yield reliability results in the desired timeframe. In some cases, it is possible to infer the reliability behavior of unfailed test samples with only the accumulated test time information and assumptions about the distribution. However, this generally leads to a great deal of uncertainty in the results. Another option in this situation is the use of degradation analysis. Degradation analysis involves the measurement and extrapolation of degradation or performance data that can be directly related to the presumed failure of the product in question. Many failure mechanisms can be directly linked to the degradation of part of the product, and degradation analysis allows the user to extrapolate to an assumed failure time based on the measurements of degradation or performance over time. To reduce testing time even further, tests can be performed at elevated stresses and the degradation at these elevated stresses can be measured resulting in a type of analysis known as accelerated degradation.
Given that products are frequently being designed with higher reliabilities and developed in shorter amounts of time, even accelerated life testing is often not sufficient to yield reliability results in the desired timeframe. In some cases, it is possible to infer the reliability behavior of unfailed test samples with only the accumulated test time information and assumptions about the distribution. However, this generally leads to a great deal of uncertainty in the results. Another option in this situation is the use of degradation analysis. Degradation analysis involves the measurement and extrapolation of degradation or performance data that can be directly related to the presumed failure of the product in question. Many failure mechanisms can be directly linked to the degradation of part of the product, and degradation analysis allows the user to extrapolate to an assumed failure time based on the measurements of degradation or performance over time. To reduce testing time even further, tests can be performed at elevated stresses and the degradation at these elevated stresses can be measured resulting in a type of analysis known as accelerated degradation.
In some cases, it is possible to directly measure the degradation over time, as with the wear of brake pads or with the propagation of crack size. In other cases, direct measurement of degradation might not be possible without invasive or destructive measurement techniques that would directly affect the subsequent performance of the product. In such cases, the degradation of the product can be estimated through the measurement of certain performance characteristics, such as using resistance to gauge the degradation of a dielectric material. In either case, however, it is necessary to be able to define a level of degradation or performance at which a failure is said to have occurred. With this failure level of performance defined, it is a relatively simple matter to use basic mathematical models to extrapolate the performance measurements over time to the point where the failure is said to occur. This is done at different stress levels, and therefore each time-to-failure is also associated with a corresponding stress level. Once the times-to-failure at the corresponding stress levels have been determined, it is merely a matter of analyzing the extrapolated failure times in the same manner as you would conventional accelerated time-to-failure data.
In some cases, it is possible to directly measure the degradation over time, as with the wear of brake pads or with the propagation of crack size. In other cases, direct measurement of degradation might not be possible without invasive or destructive measurement techniques that would directly affect the subsequent performance of the product. In such cases, the degradation of the product can be estimated through the measurement of certain performance characteristics, such as using resistance to gauge the degradation of a dielectric material. In either case, however, it is necessary to be able to define a level of degradation or performance at which a failure is said to have occurred. With this failure level of performance defined, it is a relatively simple matter to use basic mathematical models to extrapolate the performance measurements over time to the point where the failure is said to occur. This is done at different stress levels, and therefore each time-to-failure is also associated with a corresponding stress level. Once the times-to-failure at the corresponding stress levels have been determined, it is merely a matter of analyzing the extrapolated failure times in the same manner as you would conventional accelerated time-to-failure data.
Line 66: Line 58:
   Gompertz\ \ : & y=a\cdot {{b}^{cx}}  \\
   Gompertz\ \ : & y=a\cdot {{b}^{cx}}  \\
   Lloyd-Lipow\ \ : & y=a-b/x  \\
   Lloyd-Lipow\ \ : & y=a-b/x  \\
\end{matrix}</math></center>
\end{matrix}\,\!</math></center>


where <math>y</math> represents the performance, <math>x</math> represents time, and <math>a</math> and <math>b</math> are model parameters to be solved for.
where <math>y\,\!</math> represents the performance, <math>x\,\!</math> represents time, and <math>a\,\!</math> and <math>b\,\!</math> are model parameters to be solved for.
Once the model parameters <math>{{a}_{i}}</math> and <math>{{b}_{i}}</math> (and <math>{{c}_{i}}</math> for Lloyd-Lipow) are estimated for each sample <math>i</math> , a time, <math>{{x}_{i}},</math> can be extrapolated that corresponds to the defined level of failure <math>y</math> . The computed <math>{{x}_{i}}</math> can now be used as our times-to-failure for subsequent accelerated life data analysis. As with any sort of extrapolation, one must be careful not to extrapolate too far beyond the actual range of data in order to avoid large inaccuracies (modeling errors).
Once the model parameters <math>{{a}_{i}}\,\!</math> and <math>{{b}_{i}}\,\!</math> (and <math>{{c}_{i}}\,\!</math> for Lloyd-Lipow) are estimated for each sample <math>i\,\!</math>, a time, <math>{{x}_{i}},\,\!</math> can be extrapolated that corresponds to the defined level of failure <math>y\,\!</math>. The computed <math>{{x}_{i}}\,\!</math> can now be used as our times-to-failure for subsequent accelerated life data analysis. As with any sort of extrapolation, one must be careful not to extrapolate too far beyond the actual range of data in order to avoid large inaccuracies (modeling errors).


One may also define a censoring time past which no failure times are extrapolated. In practice, there is usually a rather narrow band in which this censoring time has any practical meaning. With a relatively low censoring time, no failure times will be extrapolated, which defeats the purpose of degradation analysis. A relatively high censoring time would occur after all of the theoretical failure times, thus being rendered meaningless. Nevertheless, certain situations may arise in which it is beneficial to be able to censor the accelerated degradation data.
One may also define a censoring time past which no failure times are extrapolated. In practice, there is usually a rather narrow band in which this censoring time has any practical meaning. With a relatively low censoring time, no failure times will be extrapolated, which defeats the purpose of degradation analysis. A relatively high censoring time would occur after all of the theoretical failure times, thus being rendered meaningless. Nevertheless, certain situations may arise in which it is beneficial to be able to censor the accelerated degradation data.


 
<div class="noprint">
See an example of a Degradation analysis. View it in '''[http://www.reliasoft.com/alta/examples/rc3/index.htm HTML]''' or        '''[http://www.reliasoft.tv/alta/appexamples/alta_app_ex_4.html Video]'''
{{Examples Box|ALTA_Examples|<p>More application examples are available! See also:</p>  
 
{{Examples Both|http://www.reliasoft.com/alta/examples/rc3/index.htm|Accelerated Degradation|http://www.reliasoft.tv/alta/appexamples/alta_app_ex_4.html|Watch the video...}}<nowiki/>
=Accelerated Life Test Plans=
}}
Poor accelerated test plans waste time, effort and money and may not even yield the desired information. Before starting an accelerated test (which is sometimes an expensive and difficult endeavor), it is advisable to have a plan that helps in accurately estimating reliability at operating conditions while minimizing test time and costs. A test plan should be used to decide on the appropriate stress levels that should be used (for each stress type) and the amount of the test units that need to be allocated to the different stress levels (for each combination of the different stress types' levels). This section presents some common test plans for one-stress and two-stress accelerated tests.
</div>
 
==General Assumptions==
 
Most accelerated life testing plans use the following model and testing assumptions that correspond to many practical quantitative accelerated life testing problems.
 
1. The log-time-to-failure for each unit follows a location-scale distribution such that:
 
::<math>\underset{}{\overset{}{\mathop{\Pr }}}\,(Y\le y)=\Phi \left( \frac{y-\mu }{\sigma } \right)</math>
 
where  <math>\mu </math>  and  <math>\sigma </math>  are the location and scale parameters respectively and  <math>\Phi </math> ( <math>\cdot </math> ) is the standard form of the location-scale distribution.
 
2. Failure times for all test units, at all stress levels, are statistically independent.
 
3. The location parameter  <math>\mu </math>  is a linear function of stress. Specifically, it is assumed that:
 
::<math>\begin{align}
\mu =\mu ({{z}_{1}})={{\gamma }_{0}}+{{\gamma }_{1}}x
\end{align}</math>
 
4. The scale parameter,  <math>\sigma ,</math>  does not depend on the stress levels. All units are tested until a pre-specified test time.
 
5. Two of the most common models used in quantitative accelerated life testing are the linear Weibull and lognormal models. The Weibull model is given by:
 
::<math>Y\sim SEV\left[ \mu (z)={{\gamma }_{0}}+{{\gamma }_{1}}x,\sigma  \right]</math>
 
where  <math>SEV</math>  denotes the smallest extreme value distribution. The lognormal model is given by:
 
::<math>Y\sim Normal\left[ \mu (z)={{\gamma }_{0}}+{{\gamma }_{1}}z,\sigma  \right]</math>
 
That is, log life  <math>Y</math>  is assumed to have either an  <math>SEV</math>  or a normal distribution with location parameter  <math>\mu (z)</math> , expressed as a linear function of  <math>z</math>  and constant scale parameter  <math>\sigma </math> .
 
==Planning Criteria and Problem Formulation==
 
Without loss of generality, a stress can be standardized as follows:
 
::<math>\xi =\frac{x-{{x}_{D}}}{{{x}_{H}}-{{x}_{D}}}</math>
 
where:
 
*<math>{{x}_{D}}</math>  is the use stress or design stress at which product life is of primary interest.
 
*<math>{{x}_{H}}</math>  is the highest test stress level.
The values of  <math>x</math> ,  <math>{{x}_{D}}</math>  and  <math>{{x}_{H}}</math>  refer to the actual values of stress or to the transformed values in case a transformation (e.g., the reciprocal transformation to obtain the Arrhenius relationship or the log transformation to obtain the power relationship) is used.
 
Typically, there will be a limit on the highest level of stress for testing because the distribution and life-stress relationship assumptions hold only for a limited range of the stress. The highest test level of stress,  <math>{{x}_{H}},</math>  can be determined based on engineering knowledge, preliminary tests or experience with similar products. Higher stresses will help end the test faster, but might violate your distribution and life-stress relationship assumptions.
 
Therefore,  <math>\xi =0</math>  at the design stress and  <math>\xi =1</math>  at the highest test stress.
 
A common purpose of an accelerated life test experiment is to estimate a particular percentile (unreliability value of  <math>p</math> ),  <math>{{T}_{p}}</math> , in the lower tail of the failure distribution at use stress. Thus a natural criterion is to minimize  <math>Var({{\hat{T}}_{p}})</math>  or  <math>Var({{\hat{Y}}_{p}})</math>  such that  <math>{{Y}_{p}}=\ln ({{T}_{p}})</math> .  <math>Var({{\hat{Y}}_{p}})</math>  measures the precision of the  <math>p</math>  quantile estimator; smaller values mean less variation in the value of  <math>{{\hat{Y}}_{p}}</math>  in repeated samplings. Hence a good test plan should yield a relatively small, if not the minimum,  <math>Var({{\hat{Y}}_{p}})</math>  value. For the minimization problem, the decision variables are  <math>{{\xi }_{i}}</math>  (the standardized stress level used in the test) and  <math>{{\pi }_{i}}</math>  (the percentage of the total test units allocated at that level). The optimization problem can be formulized as follows.
 
Minimize:
 
::<math>Var({{\hat{Y}}_{p}})=f({{\xi }_{i}},{{\pi }_{i}})</math>
 
Subject to:
 
::<math>0\le {{\pi }_{i}}\le 1,\text{ }i=1,2,...n</math>
 
where:
 
::<math>\underset{i=1}{\overset{n}{\mathop{\sum }}}\,{{\pi }_{i}}=1</math>
 
An optimum accelerated test plan requires algorithms to minimize  <math>Var({{\hat{Y}}_{p}})</math> .
 
Planning tests may involve compromise between efficiency and extrapolation. More failures correspond to better estimation efficiency, requiring higher stress levels but more extrapolation to the use condition. Choosing the best plan to consider must take into account the trade-offs between efficiency and extrapolation. Test plans with more stress levels are more robust than plans with fewer stress levels because they rely less on the validity of the life-stress relationship assumption. However, test plans with fewer stress levels can be more convenient.
 
 
==Test Plans for a Single Stress Type==
 
This section presents a discussion of  some of the most popular test plans used when only one stress factor is applied in the test. In order to design a test, the following information needs to be determined beforehand:
 
1. The design stress,  <math>{{x}_{D}},</math>  and the highest test stress,  <math>{{x}_{H}}</math> .
 
2. The test duration (or censoring time),  <math>\Upsilon </math> .
 
3. The probability of failure at  <math>{{x}_{D}}</math>  <math>(\xi =0)</math>  by  <math>\Upsilon </math> , denoted as  <math>{{P}_{D}},</math>  and at  <math>{{x}_{H}}</math>  <math>(\xi =1)</math>  by  <math>\Upsilon </math> , denoted as  <math>{{P}_{H}}</math> .
 
===Two Level Statistically Optimum Plan===
 
The Two Level Statistically Optimum Plan is the most important plan, as almost all other plans are derived from it. For this plan, the highest stress,  <math>{{x}_{H}}</math> , and the design stress,  <math>{{x}_{D}}</math> , are pre-determined. The test is conducted at two levels. The high test level is fixed at  <math>{{x}_{H}}</math> . The low test stress,  <math>{{x}_{L}}</math> , together with the proportion of the test units allocated to the low level,  <math>{{\pi }_{L}}</math> , are calculated such that  <math>Var({{\hat{Y}}_{p}})</math>  is minimized. Meeker [[Reference Appendix D: References|[36]]] presents more details about this test plan.
 
===Three Level Best Standard Plan===
 
In this plan, three stress levels are used. Let us use  <math>{{\xi }_{L}},</math>  <math>{{\xi }_{M}}</math>  and  <math>{{\xi }_{H}}</math>  to denote the three standardized stress levels from lowest to highest with:
 
::<math>{{\xi }_{M}}=\frac{{{\xi }_{L}}+{{\xi }_{H}}}{2}=\frac{{{\xi }_{L}}+1}{2}</math>
 
An equal number of units is tested at each level,  <math>{{\pi }_{L}}={{\pi }_{M}}={{\pi }_{H}}=1/3</math> . Therefore, the test plan is  <math>({{\xi }_{L}},{{\xi }_{M}}</math> , <math>{{\xi }_{H}},{{\pi }_{L}},{{\pi }_{M}},{{\pi }_{H}})=({{\xi }_{L}},\tfrac{{{\xi }_{L}}+1}{2}</math> , <math>1,1/3,1/3,1/3)</math>  with  <math>{{\xi }_{L}}</math>  being the only decision variable.  <math>{{\xi }_{L}}</math>  is determined such that  <math>Var({{\hat{Y}}_{p}})</math>  is minimized. Escobar [[Reference Appendix D: References|[37]]] presents more details about this test plan.
 
===Three Level Best Compromise Plan===
 
In this plan, three stress levels are used  <math>({{\xi }_{L}},\tfrac{{{\xi }_{L}}+1}{2}</math> , <math>1).</math>  <math>{{\pi }_{M}}</math> , which is a value between 0 and 1, is pre-determined.  <math>{{\pi }_{M}}=0.1</math>  and  <math>{{\pi }_{M}}=0.2</math>  are commonly used; values less than or equal to 0.2 can give good results. The test plan is
<math>({{\xi }_{L}},{{\xi }_{M}}</math> , <math>{{\xi }_{H}},{{\pi }_{L}},{{\pi }_{M}},{{\pi }_{H}})</math>  =  <math>({{\xi }_{L}},\tfrac{{{\xi }_{L}}+1}{2}</math> , <math>1,{{\pi }_{L}},{{\pi }_{M}},1-{{\pi }_{L}}-{{\pi }_{M}})</math>  with  <math>{{\xi }_{L}}</math>  and  <math>{{\pi }_{L}}</math>  being the decision variables determined such that  <math>Var({{\hat{Y}}_{p}})</math> is minimized. Meeker [[Reference Appendix D: References|[38]]] presents more details about this test plan.
 
===Three Level Best Equal Expected Number Failing Plan===
 
In this plan, three stress levels are used  <math>({{\xi }_{L}},\tfrac{{{\xi }_{L}}+1}{2}</math> , <math>1)</math>  and there is a constraint that an equal number of failures at each stress level is expected. The constraint can be written as:
 
::<math>\begin{align}
{{\pi }_{L}}{{P}_{L}}={{\pi }_{M}}{{P}_{M}}={{\pi }_{H}}{{P}_{H}}
\end{align}</math>
 
where  <math>{{P}_{L}}</math>, <math>{{P}_{M}}</math>  and <math>{{P}_{H}}</math>  are the failure probability at the low, middle and high test level, respectively.  <math>{{P}_{L}}</math>  and  <math>{{P}_{M}}</math>  can be expressed in terms of  <math>{{\xi }_{L}}</math>  and  <math>{{\xi }_{M}}</math> . Therefore, all variables can be expressed in terms of  <math>{{\xi }_{L}},</math>  which is chosen such that  <math>Var({{\hat{Y}}_{p}})</math> is minimized. Meeker [[Reference Appendix D: References|[38]]] presents more details about this test plan.
 
===Three Level 4:2:1 Allocation Plan===
 
In this plan, three stress levels  are used  <math>({{\xi }_{L}},\tfrac{{{\xi }_{L}}+1}{2}</math> , <math>1).</math>  The allocation of units at each level is pre-given as  <math>{{\pi }_{L}} : {{\pi }_{M}} : {{\pi }_{H}}=4 : 2 : 1</math> . Therefore  <math>{{\pi }_{L}}=4/7,</math>  <math>{{\pi }_{M}}=2/7</math>  and  <math>{{\pi }_{H}}=1/7</math> .  <math>{{\xi }_{L}}</math>  is the only decision variable that is chosen such that  <math>Var({{\hat{Y}}_{p}})</math>  is minimized. The optimum  <math>{{\xi }_{L}}</math>  can also be multiplied by a constant  <math>k</math>  (defined by the user) to make the low stress level closer to the use stress than to the optimized plan, in order to make a better extrapolation at the use stress. Meeker [[Reference Appendix D: References|[39]]] presents more details about this test plan.
 
===One Stress Test Plan Example===
{{:ALTA_Test_Plan_Example}}
 
==Test Plans for Two Stress Types==
 
This section presents a discussion of some of the most popular test plans used when two stress factors are applied in the test and interactions are assumed not to exists between the factors. The location parameter  <math>\mu </math>  can be expressed as function of stresses  <math>{{x}_{1}}</math>  and  <math>{{x}_{2}}</math>  or as a function of their normalized stress levels as follows:
 
::<math>\begin{align}
\mu ={{\gamma }_{0}}+{{\gamma }_{1}}{{\xi }_{1}}+{{\gamma }_{2}}{{\xi }_{2}}
\end{align}</math>
 
In order to design a test, the following information needs to be determined beforehand:
 
1. The stress limits (the design stress,  <math>{{x}_{D}},</math>  and the highest test stress,  <math>{{x}_{H}}</math> ) of each stress type.
 
2. The test time (or censoring time),  <math>\Upsilon </math>. .
 
3. The probability of failure at  <math>\Upsilon </math>  at three stress combinations. Usually  <math>{{P}_{DD}}</math> ,  <math>{{P}_{HD}}</math>  and  <math>{{P}_{DH}}</math>  are used ( <math>P</math>  indicates probability and the subscript  <math>D</math>  represents the design stress, while  <math>H</math>  represents the highest stress level in the test).
 
For two-stress test planning, two methods are available: the Three Level Optimum Plan and the
Five Level Best Compromise Plan.
 
====Three Level Optimum Plan====
 
The Three Level Optimum Plan is obtained by first finding a one-stress degenerate Two Level Statistically Optimum Plan and splitting this degenerate plan into an appropriate two-stress plan. In a degenerate test plan, the test is conducted at any two (or more) stress level combinations on a line with slope  <math>s</math>  that passes through the design  <math>{{\xi }_{D}}=\left( {{\xi }_{1D}},{{\xi }_{2D}} \right)</math> . Therefore, in the case of a degenerate design, we have:
 
::<math>\mu ={{\gamma }_{0}}+\left( {{\gamma }_{1}}+{{\gamma }_{2}}s \right){{\xi }_{1}}</math>
 
Degenerate plans help reducing the two-stress problem into a one-stress problem. Although these degenerate plans do not allow the estimation of all the model parameters and would be an unlikely choice in practice, they are used as a starting point for developing more reasonable optimum and compromise test plans. After finding the one stress degenerate Two Level Statistically Optimum Plan using the methodology explained in 13.4.3.1, the plan is split into an appropriate Three Level Optimum Plan.
 
The next figure illustrates the concept of the Three Level Optimum Plan for a two-stress test.  <math>{{\xi }_{D}}</math>  is the (0,0) point.  <math>{{C}_{O}}</math>  and  <math>{{C}_{1}}</math>  are the one-stress degenerate Two Level Statistically Optimum Plan.  <math>{{C}_{1}}</math> , which corresponds to ( <math>{{\xi }_{1}}=1,{{\xi }_{2}}=1</math> ), is always used for this type of test and is the high stress level of the degenerate plan.  <math>{{C}_{O}}</math>  corresponds to the low stress level of the degenerate plan. A line,  <math>L</math> , is drawn passing through  <math>{{C}_{O}}</math>  such that all the points along the line have the same probability of failures at the end of the test with the stress levels of the  <math>{{C}_{O}}</math>  plan.  <math>{{C}_{2}}</math>  and  <math>{{C}_{3}}</math>  are then determined by obtaining the intersections of  <math>L</math>  with the boundaries of the square.
 
[[Image:ALTA13.9.png|center|250px|Three Level Optimum Plan for two stresses.]]
 
<math>{{C}_{1}}</math> ,  <math>{{C}_{2}}</math>  and  <math>{{C}_{3}}</math>  represent the the Three Level Optimum Plan. Readers are encouraged to review Escobar [[Reference Appendix D: References|[37]]] for more details about this test plan.
 
====Five Level Best Compromise Plan====
 
The Five Level Best Compromise Plan is obtained by first finding a degenerate one-stress Three Level Best Compromise Plan, using the methodology explained in the [[Additional Tools#Three Level Best Compromise Plan|Three Level Best Compromise Plan ]](with <math>{{\pi }_{M}}=0.2</math>) , and splitting this degenerate plan into an appropriate two-stress plan.
 
In the next figure,  <math>{{\xi }_{D}}</math>  is the (0,0) point.  <math>{{C}_{O1}},{{C}_{O2}}</math>  and  <math>{{C}_{1}}</math>  are the degenerate one-stress Three Level Best Compromise Plan. Points along the  <math>{{L}_{1}}</math>  line have the same probability of failure at the end of the  <math>{{C}_{O1}}</math>  test plan, while points on  <math>{{L}_{2}}</math>  have the same probability of failure at the end of the  <math>{{C}_{O2}}</math>  test plan.  <math>{{C}_{2}},{{C}_{3}}</math> ,  <math>{{C}_{4}}</math>  and  <math>{{C}_{5}}</math>  are then determined by obtaining the intersections of  <math>{{L}_{1}}</math>  and  <math>{{L}_{2}}</math>  with the boundaries of the square.
 
[[Image:ALTA13.92.png|center|300px|Five level optimal test plan for two stresses.]]
 
<math>{{C}_{1}}</math> ,  <math>{{C}_{2}},{{C}_{3}}</math> ,  <math>{{C}_{4}}</math>  and  <math>{{C}_{5}}</math>  represent the the Five Level Best Compromise Plan. Readers are encouraged to review Escobar [[Reference Appendix D: References|[37]]] for more details about this test plan.
 
 
See an example of a test plan for two stresses. View it in '''[http://www.reliasoft.com/alta/examples/rc7/index.htm HTML]''' or        '''[http://www.reliasoft.tv/alta/appexamples/alta_app_ex_7.html Video]'''
 
==Test Plan Evaluation==
 
In addition to assessing  <math>Var({{\hat{T}}_{p}})</math> ( <math>Var({{\hat{T}}_{p}})</math>  is explained [[Additional Tools#Planning Criteria and Problem Formulation|here]]) an accelerated test plan can also be evaluated based on three different criteria. These criteria can be assessed before conducting a test to decide whether a test plan is satisfactory or whether some modifications would be beneficial. In the Control Panel of the Test Plan folio, the analyst can solve for any one of three criteria (confidence level, bounds ratio or sample size) given the two other criteria. The bounds ratio is defined as follows:
 
::<math>\text{Bounds Ratio}=\frac{\text{Two Sided Upper Bound on }{{T}_{p}}}{\text{Two Sided Lower Bound on }{{T}_{p}}}</math>
 
This ratio is analogous to the ratio that can be calculated if a test is conducted and life data are obtained and used to calculate the ratio of the confidence bounds based on the results.
 
Let us use the [[Additional Tools#One Stress Test Plan Example|example]] that was presented earlier for illustration. For example, if a 90% confidence is desired and 40 units are to be used in the test, then the bounds ratio is calculated as 2.946345,  as shown next.
 
[[Image:ALTA13.13.gif|thumb|center|400px|Evaluating the test plan using a bounds ratio criterion.]]
 
If this calculated bounds ratio is unsatisfactory, the analyst can calculate the required number of units that would meet a certain bounds ratio criterion. For example, if a bounds ratio of 2 is desired, the required sample size is calculated as 97.210033, as shown next.
 
[[Image:ALTA13.14.gif|thumb|center|400px|Evaluation the test plan using a sample size criterion.]]
 
If the sample size is kept at 40 units and a bounds ratio of 2 is desired, the equivalent confidence level we have in the test drops to 70.8629%, as shown next.
 
 
[[Image:ALTA13.15.gif|thumb|center|400px|Evaluating the test plan using a confidence level criterion.]]

Latest revision as of 00:33, 16 March 2023

New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images, more targeted search and the latest content available as a PDF. As of September 2023, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest reference at help.reliasoft.com/reference/accelerated_life_testing_data_analysis

Chapter 11: Additional Tools


ALTAbox.png

Chapter 11  
Additional Tools  

Synthesis-icon.png

Available Software:
ALTA

Examples icon.png

More Resources:
ALTA Examples

Common Shape Parameter Likelihood Ratio Test

In order to assess the assumption of a common shape parameter among the data obtained at various stress levels, the likelihood ratio (LR) test can be utilized, as described in Nelson [28]. This test applies to any distribution with a shape parameter. In the case of ALTA, it applies to the Weibull and lognormal distributions. When Weibull is used as the underlying life distribution, the shape parameter, [math]\displaystyle{ \beta ,\,\! }[/math] is assumed to be constant across the different stress levels (i.e., stress independent). Similarly, [math]\displaystyle{ {{\sigma }_{{{T}'}}}\,\! }[/math], the parameter of the lognormal distribution is assumed to be constant across the different stress levels.

The likelihood ratio test is performed by first obtaining the LR test statistic, [math]\displaystyle{ T\,\! }[/math]. If the true shape parameters are equal, then the distribution of [math]\displaystyle{ T\,\! }[/math] is approximately chi-square with [math]\displaystyle{ n-1\,\! }[/math] degrees of freedom, where [math]\displaystyle{ n\,\! }[/math] is the number of test stress levels with two or more exact failure points. The LR test statistic, [math]\displaystyle{ T\,\! }[/math], is calculated as follows:

[math]\displaystyle{ T=2({{\hat{\Lambda }}_{1}}+...+{{\hat{\Lambda }}_{n}}-{{\hat{\Lambda }}_{0}})\,\! }[/math]

where [math]\displaystyle{ \hat{\Lambda}_{1}, ..., \hat{\Lambda}_{n}\,\! }[/math] are the likelihood values obtained by fitting a separate distribution to the data from each of the [math]\displaystyle{ n\,\! }[/math] test stress levels (with two or more exact failure times). The likelihood value, [math]\displaystyle{ {{\hat{\Lambda }}_{0}},\,\! }[/math] is obtained by fitting a model with a common shape parameter and a separate scale parameter for each of the [math]\displaystyle{ n\,\! }[/math] stress levels, using indicator variables.

Once the LR statistic has been calculated, then:

  • If [math]\displaystyle{ T\le {{\chi }^{2}}(1-\alpha ;n-1),\,\! }[/math] the [math]\displaystyle{ n\,\! }[/math] shape parameter estimates do not differ statistically significantly at the 100 [math]\displaystyle{ \alpha %\,\! }[/math] level.
  • If [math]\displaystyle{ T\gt {{\chi }^{2}}(1-\alpha ;n-1),\,\! }[/math] the [math]\displaystyle{ n\,\! }[/math] shape parameter estimates differ statistically significantly at the 100 [math]\displaystyle{ \alpha %\,\! }[/math] level.


[math]\displaystyle{ {{\chi }^{2}}(1-\alpha ;n-1)\,\! }[/math] is the 100(1- [math]\displaystyle{ \alpha)\,\! }[/math] percentile of the chi-square distribution with [math]\displaystyle{ n-1\,\! }[/math] degrees of freedom.


Example: Likelihood Ratio Test Example

Consider the following times-to-failure data at three different stress levels.

Stress 406 K 416 K 426 K
Time Failed (hrs) 248 164 92
456 176 105
528 289 155
731 319 184
813 340 219
543 235


The data set was analyzed using an Arrhenius-Weibull model. The analysis yields:

[math]\displaystyle{ \widehat{\beta }=\ 2.965820\,\! }[/math]
[math]\displaystyle{ \widehat{B}=\ 10,679.567542\,\! }[/math]
[math]\displaystyle{ \widehat{C}=\ 2.396615\cdot {{10}^{-9}}\,\! }[/math]

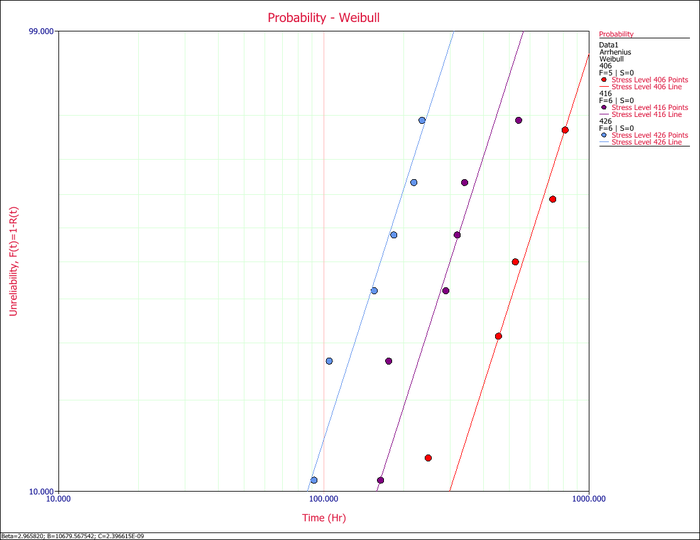
The assumption of a common [math]\displaystyle{ \beta \,\! }[/math] across the different stress levels can be visually assessed by using a probability plot. As you can see in the following plot, the plotted data from the different stress levels seem to be fairly parallel.

Probability plot of the three test stress levels.

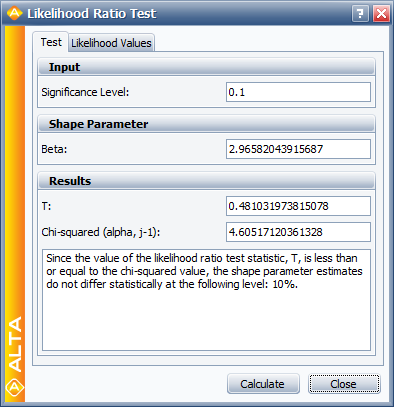
A better assessment can be made with the LR test, which can be performed using the Likelihood Ratio Test tool in ALTA. For example, in the following figure, the [math]\displaystyle{ \beta s\,\! }[/math] are compared for equality at the 10% level.

Lkt.png

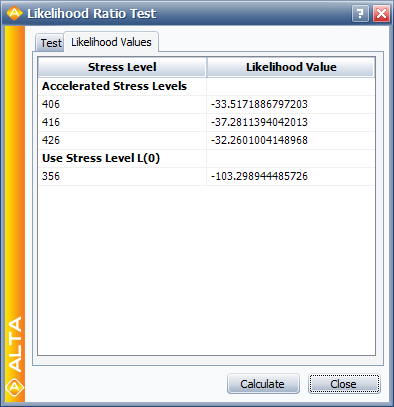
The LR test statistic, [math]\displaystyle{ T\,\! }[/math], is calculated to be 0.481. Therefore, [math]\displaystyle{ T=0.481\le 4.605={{\chi }^{2}}(0.9;2),\,\! }[/math] the [math]\displaystyle{ {\beta }'\,\! }[/math] s do not differ significantly at the 10% level. The individual likelihood values for each of the test stresses are shown next.

Lktr.png

Tests of Comparison

It is often desirable to be able to compare two sets of accelerated life data in order to determine which of the data sets has a more favorable life distribution. The units from which the data are obtained could either be from two alternate designs, alternate manufacturers or alternate lots or assembly lines. Many methods are available in statistical literature for doing this when the units come from a complete sample, (i.e., a sample with no censoring). This process becomes a little more difficult when dealing with data sets that have censoring, or when trying to compare two data sets that have different distributions. In general, the problem boils down to that of being able to determine any statistically significant difference between the two samples of potentially censored data from two possibly different populations. This section discusses some of the methods that are applicable to censored data, and are available in ALTA.

Simple Plotting

One popular graphical method for making this determination involves plotting the data at a given stress level with confidence bounds and seeing whether the bounds overlap or separate at the point of interest. This can be effective for comparisons at a given point in time or a given reliability level, but it is difficult to assess the overall behavior of the two distributions, as the confidence bounds may overlap at some points and be far apart at others. This can be easily done using the overlay plot feature in ALTA.

Using the Life Comparison Wizard

Another methodology, suggested by Gerald G. Brown and Herbert C. Rutemiller, is to estimate the probability of whether the times-to-failure of one population are better or worse than the times-to-failure of the second. The equation used to estimate this probability is given by:

[math]\displaystyle{ P\left[ {{t}_{2}}\ge {{t}_{1}} \right]=\int_{0}^{\infty }{{f}_{1}}(t)\cdot {{R}_{2}}(t)\cdot dt\,\! }[/math]

where [math]\displaystyle{ {{f}_{1}}(t)\,\! }[/math] is the pdf of the first distribution and [math]\displaystyle{ {{R}_{2}}(t)\,\! }[/math] is the reliability function of the second distribution. The evaluation of the superior data set is based on whether this probability is smaller or greater than 0.50. If the probability is equal to 0.50, then is equivalent to saying that the two distributions are identical.

For example, consider two alternate designs, where X and Y represent the life test data from each design. If we simply wanted to choose the component with the higher reliability, we could simply select the component with the higher reliability at time [math]\displaystyle{ t\,\! }[/math]. However, if we wanted to design the product to be as long-lived as possible, we would want to calculate the probability that the entire distribution of one design is better than the other. The statement "the probability that X is greater than or equal to Y" can be interpreted as follows:

  • If [math]\displaystyle{ P=0.50\,\! }[/math], then the statement is equivalent to saying that both X and Y are equal.
  • If [math]\displaystyle{ P\lt 0.50\,\! }[/math] or, for example, [math]\displaystyle{ P=0.10\,\! }[/math], then the statement is equivalent to saying that [math]\displaystyle{ P=1-0.10=0.90\,\! }[/math], or Y is better than X with a 90% probability.

ALTA's Comparison Wizard allows you to perform such calculations. The comparison is performed at the given use stress levels of each data set, using the equation:

[math]\displaystyle{ P\left[ {{t}_{2}}\ge {{t}_{1}} \right]=\int_{0}^{\infty }{{f}_{1}}(t,{{V}_{Use,1}})\cdot {{R}_{2}}(t,{{V}_{Use,2}})\cdot dt\,\! }[/math]

Degradation Analysis

Given that products are frequently being designed with higher reliabilities and developed in shorter amounts of time, even accelerated life testing is often not sufficient to yield reliability results in the desired timeframe. In some cases, it is possible to infer the reliability behavior of unfailed test samples with only the accumulated test time information and assumptions about the distribution. However, this generally leads to a great deal of uncertainty in the results. Another option in this situation is the use of degradation analysis. Degradation analysis involves the measurement and extrapolation of degradation or performance data that can be directly related to the presumed failure of the product in question. Many failure mechanisms can be directly linked to the degradation of part of the product, and degradation analysis allows the user to extrapolate to an assumed failure time based on the measurements of degradation or performance over time. To reduce testing time even further, tests can be performed at elevated stresses and the degradation at these elevated stresses can be measured resulting in a type of analysis known as accelerated degradation. In some cases, it is possible to directly measure the degradation over time, as with the wear of brake pads or with the propagation of crack size. In other cases, direct measurement of degradation might not be possible without invasive or destructive measurement techniques that would directly affect the subsequent performance of the product. In such cases, the degradation of the product can be estimated through the measurement of certain performance characteristics, such as using resistance to gauge the degradation of a dielectric material. In either case, however, it is necessary to be able to define a level of degradation or performance at which a failure is said to have occurred. With this failure level of performance defined, it is a relatively simple matter to use basic mathematical models to extrapolate the performance measurements over time to the point where the failure is said to occur. This is done at different stress levels, and therefore each time-to-failure is also associated with a corresponding stress level. Once the times-to-failure at the corresponding stress levels have been determined, it is merely a matter of analyzing the extrapolated failure times in the same manner as you would conventional accelerated time-to-failure data.

Once the level of failure (or the degradation level that would constitute a failure) is defined, the degradation for multiple units over time needs to be measured (with different groups of units being at different stress levels). As with conventional accelerated data, the amount of certainty in the results is directly related to the number of units being tested, the number of units at each stress level, as well as in the amount of overstressing with respect to the normal operating conditions. The performance or degradation of these units needs to be measured over time, either continuously or at predetermined intervals. Once this information has been recorded, the next task is to extrapolate the performance measurements to the defined failure level in order to estimate the failure time. ALTA allows the user to perform such analysis using a linear, exponential, power, logarithmic, Gompertz or Lloyd-Lipow model to perform this extrapolation. These models have the following forms:

[math]\displaystyle{ \begin{matrix} Linear\ \ : & y=a\cdot x+b \\ Exponential\ \ : & y=b\cdot {{e}^{a\cdot x}} \\ Power\ \ : & y=b\cdot {{x}^{a}} \\ Logarithmic\ \ : & y=a\cdot ln(x)+b \\ Gompertz\ \ : & y=a\cdot {{b}^{cx}} \\ Lloyd-Lipow\ \ : & y=a-b/x \\ \end{matrix}\,\! }[/math]

where [math]\displaystyle{ y\,\! }[/math] represents the performance, [math]\displaystyle{ x\,\! }[/math] represents time, and [math]\displaystyle{ a\,\! }[/math] and [math]\displaystyle{ b\,\! }[/math] are model parameters to be solved for. Once the model parameters [math]\displaystyle{ {{a}_{i}}\,\! }[/math] and [math]\displaystyle{ {{b}_{i}}\,\! }[/math] (and [math]\displaystyle{ {{c}_{i}}\,\! }[/math] for Lloyd-Lipow) are estimated for each sample [math]\displaystyle{ i\,\! }[/math], a time, [math]\displaystyle{ {{x}_{i}},\,\! }[/math] can be extrapolated that corresponds to the defined level of failure [math]\displaystyle{ y\,\! }[/math]. The computed [math]\displaystyle{ {{x}_{i}}\,\! }[/math] can now be used as our times-to-failure for subsequent accelerated life data analysis. As with any sort of extrapolation, one must be careful not to extrapolate too far beyond the actual range of data in order to avoid large inaccuracies (modeling errors).

One may also define a censoring time past which no failure times are extrapolated. In practice, there is usually a rather narrow band in which this censoring time has any practical meaning. With a relatively low censoring time, no failure times will be extrapolated, which defeats the purpose of degradation analysis. A relatively high censoring time would occur after all of the theoretical failure times, thus being rendered meaningless. Nevertheless, certain situations may arise in which it is beneficial to be able to censor the accelerated degradation data.

Examples heading.png

More application examples are available! See also:

Examples link.png Accelerated Degradation or Examples movie.png Watch the video...

Retrieved from "https://www.reliawiki.com/index.php?title=Additional_Tools&oldid=65704"