Least Squares/Rank Regression Equations: Difference between revisions
Kate Racaza (talk | contribs) No edit summary |
|||
| Line 223: | Line 223: | ||
[[Image:LdaappendixA.2.gif|thumb|center|500px]] | [[Image:LdaappendixA.2.gif|thumb|center|500px]] | ||
Note that the regression on Y is not necessarily the same as the regression on X. The only time when the two regressions are the same (i.e. will yield the same equation for a line) is when the data lie perfectly on a line. | Note that the regression on Y is not necessarily the same as the regression on X. The only time when the two regressions are the same (i.e., will yield the same equation for a line) is when the data lie perfectly on a line. | ||
The correlation coefficient is given by: | The correlation coefficient is given by: | ||
Revision as of 02:56, 6 August 2012
Rank Regression on Y
Assume that a set of data pairs (x1, y1), (x2, y2), ... , (xN, yN), were obtained and plotted. Then, according to the least squares principle, which minimizes the vertical distance between the data points and the straight line fitted to the data, the best fitting straight line to these data is the straight line y = + x such that:
- [math]\displaystyle{ \sum_{i=1}^N (\hat{a}+\hat{b} x_i - y_i)^2=min(a,b)\sum_{i=1}^N (a+b x_i-y_i)^2 }[/math]
and where and are the least squares estimates of a and b, and N is the number of data points.
To obtain [math]\displaystyle{ \hat{a} }[/math] and [math]\displaystyle{ \hat{b} }[/math], let:
- [math]\displaystyle{ F=\sum_{i=1}^N (a+bx_i-y_i)^2 }[/math]
Differentiating F with respect to a and b yields:
- [math]\displaystyle{ \frac{\partial F}{\partial a}=2\sum_{i=1}^N (a+b x_i-y_i) }[/math] (1)
- and:
- [math]\displaystyle{ \frac{\partial F}{\partial b}=2\sum_{i=1}^N (a+b x_i-y_i)x_i }[/math] (2)
Setting Eqns. (1) and (2) equal to zero yields:
- [math]\displaystyle{ \sum_{i=1}^N (a+b x_i-y_i)x_i=\sum_{i=1}^N(\hat{y}_i-y_i)=-\sum_{i=1}^N(y_i-\hat{y}_i)=0 }[/math]
- and:
- [math]\displaystyle{ \sum_{i=1}^N (a+b x_i-y_i)x_i=\sum_{i=1}^N(\hat{y}_i-y_i)x_i=-\sum_{i=1}^N(y_i-\hat{y}_i)x_i =0 }[/math]
Solving the equations simultaneously yields:
- [math]\displaystyle{ \hat{a}=\frac{\displaystyle \sum_{i=1}^N y_i}{N}-\hat{b}\frac{\displaystyle \sum_{i=1}{N} x_i}{N}=\bar{y}-\hat{b}\bar{x} }[/math] (3)
- and:
- [math]\displaystyle{ \hat{b}=\frac{\displaystyle \sum{i=1}^N x_i y_i-\frac{\displaystyle \sum_{i=1}^N x_i \sum_{i=1}^N y_i}{N}}{\displaystyle \sum_{i=1}^N x_i^2-\frac{\left(\displaystyle\sum_{i=1}^N x_i\right)^2}{N}} }[/math](4)
Rank Regression on X
Assume that a set of data pairs (x1, y1), (x2, y2), ... , (xN, yN) were obtained and plotted. Then, according to the least squares principle, which minimizes the horizontal distance between the data points and the straight line fitted to the data, the best fitting straight line to these data is the straight line x = + y such that:
- [math]\displaystyle{ \displaystyle\sum_{i=1}^N(\hat{a}+\hat{b}y_i-x_i)^2=min(a,b)\displaystyle\sum_{i=1}^N (a+by_i-x_i)^2 }[/math]
Again, [math]\displaystyle{ \hat{a} }[/math] and [math]\displaystyle{ \hat{b} }[/math] are the least squares estimates of a and b, and N is the number of data points.
To obtain [math]\displaystyle{ \hat{a} }[/math] and [math]\displaystyle{ \hat{b} }[/math], let:
- [math]\displaystyle{ F=\displaystyle\sum_{i=1}^N(a+by_i-x_i)^2 }[/math]
Differentiating F with respect to a and b yields:
- [math]\displaystyle{ \frac{\partial F}{\partial a}=2\displaystyle\sum_{i=1}^N(a+by_i-x_i }[/math] (5)
- and:
- [math]\displaystyle{ \frac{\partial F}{\partial b}=2\displaystyle\sum_{i=1}^N(a+by_i-x_i)y_i }[/math](6)
Setting Eqns. (5) and (6) equal to zero yields:
- [math]\displaystyle{ \displaystyle\sum_{i=1}^N(a+by_i-x_i)=\displaystyle\sum_{i=1}^N(\widehat{x}_i-x_i)=-\displaystyle\sum_{i=1}^N(x_i-\widehat{x}_i)=0 }[/math]
- and:
- [math]\displaystyle{ \displaystyle\sum_{i=1}^N(a+by_i-x_i)y_i=\displaystyle\sum_{i=1}^N(\widehat{x}_i-x_i)y_i=-\displaystyle\sum_{i=1}^N(x_i-\widehat{x}_i)y_i=0 }[/math]
Solving the above equations simultaneously yields:
- [math]\displaystyle{ \widehat{a}=\frac{\displaystyle\sum_{i=1}^N x_i}{N}-\widehat{b}\frac{\displaystyle\sum_{i=1}^N y_i}{N}=\bar{x}-\widehat{b}\bar{y} }[/math](7)
- and:
- [math]\displaystyle{ \widehat{b}=\frac{\displaystyle\sum_{i=1}^N x_iy_i-\frac{\displaystyle\sum_{i=1}^N x_i\displaystyle\sum_{i=1}^N y_i}{N}}{\displaystyle\sum_{i=1}^N y_i^2-\frac{\left(\displaystyle\sum_{i=1}^N y_i\right)^2}{N}} }[/math](8)
Solving the equation of the line for y yields:
- [math]\displaystyle{ y=-\frac{\hat{a}}{\hat{b}}+\frac{1}{\hat{b}} x }[/math]
Example
Fit a least squares straight line using regression on X and regression on Y to the following data:
| x | 1 | 2.5 | 4 | 6 | 8 | 9 | 11 | 15 |
|---|---|---|---|---|---|---|---|---|
| y | 1.5 | 2 | 4 | 4 | 5 | 7 | 8 | 10 |
The first step is to generate the following table:
| [math]\displaystyle{ i }[/math] | [math]\displaystyle{ x_i }[/math] | [math]\displaystyle{ y_i }[/math] | [math]\displaystyle{ x_i^2 }[/math] | [math]\displaystyle{ x_iy_i }[/math] | [math]\displaystyle{ y_i^2 }[/math] |
|---|---|---|---|---|---|
| 1 | 1 | 1.5 | 1 | 1.5 | 2.25 |
| 2 | 2.5 | 2 | 6.25 | 5 | 4 |
| 3 | 4 | 4 | 16 | 16 | 16 |
| 4 | 6 | 4 | 36 | 24 | 16 |
| 5 | 8 | 5 | 64 | 40 | 25 |
| 6 | 9 | 7 | 81 | 63 | 49 |
| 7 | 11 | 8 | 121 | 88 | 64 |
| 8 | 15 | 10 | 225 | 150 | 100 |
| [math]\displaystyle{ \Sigma }[/math] | 56.5 | 41.5 | 550.25 | 387.5 | 276.25 |
From the table then, and for rank regression on Y (RRY):
- [math]\displaystyle{ \widehat{b}=\frac{387.5-(56.5)(41.5)/8}{550.25-(56.5)^2/8} }[/math]
- [math]\displaystyle{ \widehat{b}=0.6243 }[/math]
- and:
- [math]\displaystyle{ \widehat{a}=\frac{41.5}{8}-0.6243\frac{56.5}{8} }[/math]
- [math]\displaystyle{ \widehat{a}=0.77836 }[/math]
The least squares line is given by:
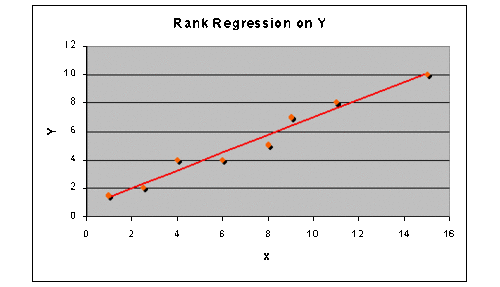
- [math]\displaystyle{ y=0.77836+0.6243x }[/math]
The plotted line is shown in the next figure.
For rank regression on X (RRX) using the same table yields:
- [math]\displaystyle{ \widehat{b}=\frac{387.5-(56.5)(41.5)/8}{276.25-(41.5)^2/8} }[/math]
- [math]\displaystyle{ \widehat{a}=-0.97002 }[/math]
- and:
- [math]\displaystyle{ \widehat{a}=\frac{56.5}{8}-1.5484\frac{41.5}{8} }[/math]
- \widehat{a}=-0.97002
The least squares line is given by:
- [math]\displaystyle{ y=-\frac{(-0.97002)}{1.5484}+\frac{1}{1.5484}\cdot x }[/math]
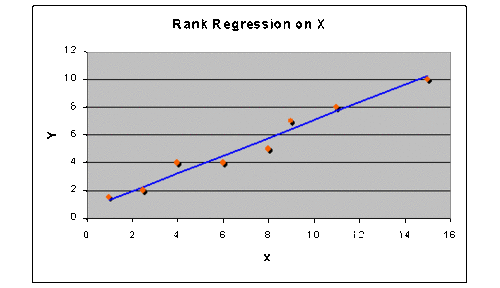
- [math]\displaystyle{ y=0.62645+0.64581\cdot x }[/math]
The plotted line is shown in the next figure.
Note that the regression on Y is not necessarily the same as the regression on X. The only time when the two regressions are the same (i.e., will yield the same equation for a line) is when the data lie perfectly on a line.
The correlation coefficient is given by:
- [math]\displaystyle{ \hat{\rho}=\frac{\displaystyle\sum_{i=1}^N x_iy_i-\frac{\displaystyle\sum_{i=1}^N x_i\displaystyle\sum_{i=1}^N y_i}{N}}{\sqrt{\left(\displaystyle\sum_{i=1}^N x_i^2-\frac{(\displaystyle\sum_{i=1}^N x_i)^2}{N}\right)\left(\displaystyle\sum_{i=1}^N y_i^2-\frac{(\displaystyle\sum_{i=1}^N y_i)^2}{N}\right)}} }[/math]
- [math]\displaystyle{ \widehat{\rho}=\frac{387.5-(56.5)(41.5)/8}{[(550.25-(56.5)^2/8)(276.25-(41.5)^2/8)]^{\frac{1}{2}}} }[/math]
- [math]\displaystyle{ \widehat{\rho}=0.98321 }[/math]