Comparing the Standard and Modified Gompertz Models: Difference between revisions
mNo edit summary |
Lisa Hacker (talk | contribs) No edit summary |
||
| Line 1: | Line 1: | ||
<noinclude>{{Banner RGA Examples}} | <noinclude>{{Banner RGA Examples}} | ||
''This example appears in the [ | ''This example appears in the [https://help.reliasoft.com/reference/reliability_growth_and_repairable_system_analysis Reliability growth reference]''. | ||
</noinclude> | </noinclude> | ||
Latest revision as of 21:20, 18 September 2023
 |
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at RGA examples and RGA reference examples.
This example appears in the Reliability growth reference.
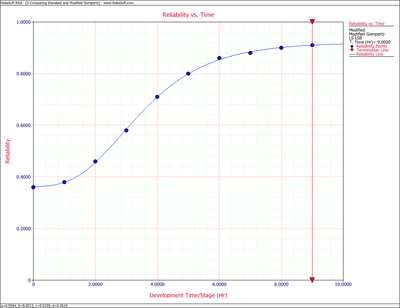
Using the data in the following table, determine whether the standard Gompertz or modified Gompertz would be better suited for analyzing the given data.
| Stage | Reliability (%) |
|---|---|
| 0 | 36 |
| 1 | 38 |
| 2 | 46 |
| 3 | 58 |
| 4 | 71 |
| 5 | 80 |
| 6 | 86 |
| 7 | 88 |
| 8 | 90 |
| 9 | 91 |
Solution
The standard Gompertz Reliability vs. Time plot is shown next.
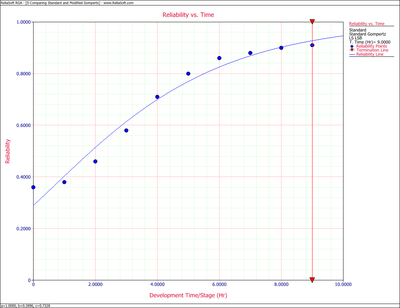
The standard Gompertz seems to do a fairly good job of modeling the data. However, it appears that it is having difficulty modeling the S-shape of the data. The modified Gompertz Reliability vs. Time plot is shown next. As expected, the modified Gompertz does a much better job of handling the S-shape presented by the data and provides a better fit for this data.