Preventive Maintenance: Difference between revisions
(Created page with 'Preventive maintenance (PM) is a schedule of planned maintenance actions aimed at the prevention of breakdowns and failures. The primary goal of preventive maintenance is to pre…') |
Lisa Hacker (talk | contribs) No edit summary |
||
| (18 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
<noinclude>{{Banner BlockSim Articles}}{{Navigation box}} | |||
''This article also appears in the [https://help.reliasoft.com/reference/system_analysis System analysis reference].'' | |||
</noinclude> | |||
Preventive maintenance (PM) is a schedule of planned maintenance actions aimed at the prevention of breakdowns and failures. The primary goal of preventive maintenance is to prevent the failure of equipment before it actually occurs. It is designed to preserve and enhance equipment reliability by replacing worn components before they actually fail. Preventive maintenance activities include equipment checks, partial or complete overhauls at specified periods, oil changes, lubrication and so on. In addition, workers can record equipment deterioration so they know to replace or repair worn parts before they cause system failure. Recent technological advances in tools for inspection and diagnosis have enabled even more accurate and effective equipment maintenance. The ideal preventive maintenance program would prevent all equipment failure before it occurs. | Preventive maintenance (PM) is a schedule of planned maintenance actions aimed at the prevention of breakdowns and failures. The primary goal of preventive maintenance is to prevent the failure of equipment before it actually occurs. It is designed to preserve and enhance equipment reliability by replacing worn components before they actually fail. Preventive maintenance activities include equipment checks, partial or complete overhauls at specified periods, oil changes, lubrication and so on. In addition, workers can record equipment deterioration so they know to replace or repair worn parts before they cause system failure. Recent technological advances in tools for inspection and diagnosis have enabled even more accurate and effective equipment maintenance. The ideal preventive maintenance program would prevent all equipment failure before it occurs. | ||
| Line 25: | Line 28: | ||
====The Fallacy of "Constant Failure Rate" and "Preventive Replacement"==== | ====The Fallacy of "Constant Failure Rate" and "Preventive Replacement"==== | ||
Even though we alluded to the fact in the last section, it is important to make it explicitly clear that if a component has a constant failure rate (i.e., defined by an exponential distribution), then preventive maintenance of the component will have no effect on the component's failure occurrences. To illustrate this, consider a component with an | Even though we alluded to the fact in the last section, it is important to make it explicitly clear that if a component has a constant failure rate (i.e., defined by an exponential distribution), then preventive maintenance of the component will have no effect on the component's failure occurrences. To illustrate this, consider a component with an <math>MTTF\,\!</math> = <math>100\,\!</math> hours, or <math>\lambda =0.01\,\!</math>, and with preventive replacement every 50 hours. The reliability vs. time graph for this case is illustrated in the following figure, where the component is replaced every 50 hours, thereby resetting the component's reliability to one. At first glance, it may seem that the preventive maintenance action is actually maintaining the component at a higher reliability. | ||
[[Image:7i2.png|center| | [[Image:7i2.png|center|500px|Reliability vs. time for a single component with an <math>MTTF =100\,\!</math> hours, or <math>\lambda =0.01\,\!</math>, and with preventive replacement every 50 hours.|link=]] | ||
However, consider the following cases for a single component: | However, consider the following cases for a single component: | ||
| Line 33: | Line 36: | ||
'''Case 1''': The component's reliability from 0 to 60 hours: | '''Case 1''': The component's reliability from 0 to 60 hours: | ||
*With preventive maintenance, the component was replaced with a new one at 50 hours so the overall reliability is based on the reliability of the new component for 10 hours, | *With preventive maintenance, the component was replaced with a new one at 50 hours so the overall reliability is based on the reliability of the new component for 10 hours, <math>R(t=10)=90.48%\,\!</math>, times the reliability of the previous component, <math>R(t=50)=60.65%\,\!</math>. The result is <math>R(t=60)=54.88%.\,\!</math> <br> | ||
*Without preventive maintenance, the reliability would be the reliability of the same component operating to 60 hours, or | *Without preventive maintenance, the reliability would be the reliability of the same component operating to 60 hours, or <math>R(t=60)=54.88%\,\!</math>.<br> | ||
<br> | <br> | ||
'''Case 2''': The component's reliability from 50 to 60 hours: | '''Case 2''': The component's reliability from 50 to 60 hours: | ||
*With preventive maintenance, the component was replaced at 50 hours, so this is solely based on the reliability of the new component for a mission of 10 hours, or | *With preventive maintenance, the component was replaced at 50 hours, so this is solely based on the reliability of the new component for a mission of 10 hours, or <math>R(t=10)=90.48%\,\!</math>.<br> | ||
*Without preventive maintenance, the reliability would be the conditional reliability of the same component operating to 60 hours, having already survived to 50 hours, or | *Without preventive maintenance, the reliability would be the conditional reliability of the same component operating to 60 hours, having already survived to 50 hours, or <math>{{R}_{C}}(t=10|T=50)=R(60)/R(50)=90.48%\,\!</math>. | ||
As can be seen, both cases — with and without preventive maintenance — yield the same results. | As can be seen, both cases — with and without preventive maintenance — yield the same results. | ||
| Line 51: | Line 54: | ||
The following figure shows the Cost Per Unit Time vs. Time plot and it can be seen that the corrective replacement costs increase as the replacement interval increases. In other words, the less often you perform a PM action, the higher your corrective costs will be. Obviously, as we let a component operate for longer times, its failure rate increases to a point that it is more likely to fail, thus requiring more corrective actions. The opposite is true for the preventive replacement costs. The longer you wait to perform a PM, the less the costs; if you do PM too often, the costs increase. If we combine both costs, we can see that there is an optimum point that minimizes the costs. In other words, one must strike a balance between the risk (costs) associated with a failure while maximizing the time between PM actions. | The following figure shows the Cost Per Unit Time vs. Time plot and it can be seen that the corrective replacement costs increase as the replacement interval increases. In other words, the less often you perform a PM action, the higher your corrective costs will be. Obviously, as we let a component operate for longer times, its failure rate increases to a point that it is more likely to fail, thus requiring more corrective actions. The opposite is true for the preventive replacement costs. The longer you wait to perform a PM, the less the costs; if you do PM too often, the costs increase. If we combine both costs, we can see that there is an optimum point that minimizes the costs. In other words, one must strike a balance between the risk (costs) associated with a failure while maximizing the time between PM actions. | ||
[[Image:costpertime.png|center| | [[Image:costpertime.png|center|500px|Cost curves for preventive and corrective replacement.|link=]] | ||
===Optimum Age Replacement Policy=== | ===Optimum Age Replacement Policy=== | ||
To determine the optimum time for such a preventive maintenance action (replacement), we need to mathematically formulate a model that describes the associated costs and risks. In developing the model, it is assumed that if the unit fails before time | To determine the optimum time for such a preventive maintenance action (replacement), we need to mathematically formulate a model that describes the associated costs and risks. In developing the model, it is assumed that if the unit fails before time <math>t\,\!</math>, a corrective action will occur and if it does not fail by time <math>t\,\!</math>, a preventive action will occur. In other words, the unit is replaced upon failure or after a time of operation, <math>t\,\!</math>, whichever occurs first. | ||
Thus, the optimum replacement time can be found by minimizing the cost per unit time, | Thus, the optimum replacement time can be found by minimizing the cost per unit time, <math>CPUT\left( t \right).\,\!</math> <math>CPUT\left( t \right)\,\!</math> is given by: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
CPUT\left( t \right)= & \frac{\text{Total Expected Replacement Cost per Cycle}}{\text{Expected Cycle Length}} \\ | CPUT\left( t \right)= & \frac{\text{Total Expected Replacement Cost per Cycle}}{\text{Expected Cycle Length}} \\ | ||
= & \frac{{{C}_{P}}\cdot R\left( t \right)+{{C}_{U}}\cdot \left[ 1-R\left( t \right) \right]}{\ | = & \frac{{{C}_{P}}\cdot R\left( t \right)+{{C}_{U}}\cdot \left[ 1-R\left( t \right) \right]}{\int_{0}^{t}R\left( s \right)ds} | ||
\end{align}</math> | \end{align}\,\!</math> | ||
where: | where: | ||
:* <math>R(t)\,\!</math> | :* <math>R(t)\,\!</math> = reliability at time <math>t\,\!</math>.<br> | ||
:* <math>{{C}_{P}}\,\!</math> | :* <math>{{C}_{P}}\,\!</math> = cost of planned replacement.<br> | ||
:* <math>{{C}_{U}}\,\!</math> | :* <math>{{C}_{U}}\,\!</math> = cost of unplanned replacement.<br> | ||
The optimum replacement time interval, | The optimum replacement time interval, <math>t\,\!</math>, is the time that minimizes <math>CPUT\left( t \right).\,\!</math> This can be found by solving for <math>t\,\!</math> such that: | ||
::<math>\frac{\partial \left[ CPUT(t) \right]}{\partial t}=0</math> | ::<math>\frac{\partial \left[ CPUT(t) \right]}{\partial t}=0\,\!</math> | ||
Or by solving for a | Or by solving for a <math>t\,\!</math> that satisfies the following equation: | ||
::<math>\frac{\partial \left[ \tfrac{{{C}_{P}}\cdot R\left( t \right)+{{C}_{U}}\cdot \left[ 1-R\left( t \right) \right]}{\ | ::<math>\frac{\partial \left[ \tfrac{{{C}_{P}}\cdot R\left( t \right)+{{C}_{U}}\cdot \left[ 1-R\left( t \right) \right]}{\int_{0}^{t}R\left( s \right)ds} \right]}{\partial t}=0\,\!</math> | ||
Interested readers can refer to [[Appendix_B:_References | | Interested readers can refer to Barlow and Hunter [[Appendix_B:_References |[2]]] for more details on this model. | ||
In BlockSim (Version 8 and above), you can use the Optimum Replacement window to determine the optimum replacement time either for an individual block or for multiple blocks in a diagram simultaneously. When working with multiple blocks, the calculations can be for individual blocks or for one or more groups of blocks. For each item that is included in the optimization calculations, you will need to specify the cost for a planned replacement and the cost for an unplanned replacement. This is done by calculating the costs for replacement based on the item settings using equations or simulation and then, if desired, manually entering any additional costs for either type of replacement in the corresponding columns of the table. | |||
The equations used to calculate the costs of planned and unplanned tasks for each item based on its associated URD are as follows: | |||
*For the cost of planned tasks, here denoted as PM cost: | *For the cost of planned tasks, here denoted as PM cost: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
\text{PM Cost}= \left(\text{PM Down Time Rate}+ \text{Block Level Down Time Rate} \right)\cdot \left( \text{MTTPM}+\text{Pool Delay} +\text{Crew Delay} \right) \\ | \text{PM Cost}= \left(\text{PM Down Time Rate}+ \text{Block Level Down Time Rate} \right) \cdot \left( \text{MTTPM}+\text{Pool Delay} +\text{Crew Delay} \right) \\ | ||
+ \text{Crew Labor Rate} \cdot \text{MTTPM} + \text{Cost per PM} + \text{Cost per Pool} +\text{Cost per Crew} | + \text{Crew Labor Rate} \cdot \text{MTTPM} + \text{Cost per PM} + \text{Cost per Pool} +\text{Cost per Crew} | ||
\end{align}</math> | \end{align}\,\!</math> | ||
:Only PM tasks based on item age or system age (fixed or dynamic intervals) are considered. If there is more than one PM task based on item age, only the first one is considered. | |||
*For the cost of the unplanned task, here denoted as CM cost: | *For the cost of the unplanned task, here denoted as CM cost: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
\text{CM Cost}= \left(\text{CM Down Time Rate}+ \text{Block Level Down Time Rate} \right)\cdot \left( \text{MTTR}+\text{Pool Delay} +\text{Crew Delay} \right) \\ | \text{CM Cost}= & \left(\text{CM Down Time Rate}+ \text{Block Level Down Time Rate} \right) \cdot \left( \text{MTTR}+\text{Pool Delay} +\text{Crew Delay} \right) \\ | ||
+ \text{Crew Labor Rate} \cdot \text{MTTR} + \text{Cost per CM} + \text{Cost per Pool} +\text{Cost per Crew} | & + \text{Crew Labor Rate} \cdot \text{MTTR} + \text{Cost per CM} + \text{Cost per Pool} +\text{Cost per Crew} +\text{Block Level Cost per Failure} | ||
+\text{Block Level Cost per Failure} | \end{align}\,\!</math> | ||
\end{align}</math> | |||
When using simulation, for costs associated with planned replacements, all preventive tasks based on item age or system age (fixed or dynamic intervals) are considered. Because each item is simulated as a system (i.e., in isolation from any other item), tasks triggered in other ways are not considered. | |||
===Example: Optimum Replacement Time=== | ===Example: Optimum Replacement Time=== | ||
{{:Optimum_Replacement_Time_Example}} | |||
Latest revision as of 21:04, 18 September 2023
 |
This article also appears in the System analysis reference.
Preventive maintenance (PM) is a schedule of planned maintenance actions aimed at the prevention of breakdowns and failures. The primary goal of preventive maintenance is to prevent the failure of equipment before it actually occurs. It is designed to preserve and enhance equipment reliability by replacing worn components before they actually fail. Preventive maintenance activities include equipment checks, partial or complete overhauls at specified periods, oil changes, lubrication and so on. In addition, workers can record equipment deterioration so they know to replace or repair worn parts before they cause system failure. Recent technological advances in tools for inspection and diagnosis have enabled even more accurate and effective equipment maintenance. The ideal preventive maintenance program would prevent all equipment failure before it occurs.
Value of Preventive Maintenance
There are multiple misconceptions about preventive maintenance. One such misconception is that PM is unduly costly. This logic dictates that it would cost more for regularly scheduled downtime and maintenance than it would normally cost to operate equipment until repair is absolutely necessary. This may be true for some components; however, one should compare not only the costs but the long-term benefits and savings associated with preventive maintenance. Without preventive maintenance, for example, costs for lost production time from unscheduled equipment breakdown will be incurred. Also, preventive maintenance will result in savings due to an increase of effective system service life.
Long-term benefits of preventive maintenance include:
- • Improved system reliability.
- • Decreased cost of replacement.
- • Decreased system downtime.
- • Better spares inventory management.
Long-term effects and cost comparisons usually favor preventive maintenance over performing maintenance actions only when the system fails.
When Does Preventive Maintenance Make Sense?
Preventive maintenance is a logical choice if, and only if, the following two conditions are met:
- Condition #1: The component in question has an increasing failure rate. In other words, the failure rate of the component increases with time, implying wear-out. Preventive maintenance of a component that is assumed to have an exponential distribution (which implies a constant failure rate) does not make sense!
- Condition #2: The overall cost of the preventive maintenance action must be less than the overall cost of a corrective action.
If both of these conditions are met, then preventive maintenance makes sense. Additionally, based on the costs ratios, an optimum time for such action can be easily computed for a single component. This is detailed in later sections.
The Fallacy of "Constant Failure Rate" and "Preventive Replacement"
Even though we alluded to the fact in the last section, it is important to make it explicitly clear that if a component has a constant failure rate (i.e., defined by an exponential distribution), then preventive maintenance of the component will have no effect on the component's failure occurrences. To illustrate this, consider a component with an [math]\displaystyle{ MTTF\,\! }[/math] = [math]\displaystyle{ 100\,\! }[/math] hours, or [math]\displaystyle{ \lambda =0.01\,\! }[/math], and with preventive replacement every 50 hours. The reliability vs. time graph for this case is illustrated in the following figure, where the component is replaced every 50 hours, thereby resetting the component's reliability to one. At first glance, it may seem that the preventive maintenance action is actually maintaining the component at a higher reliability.
![Reliability vs. time for a single component with an [math]\displaystyle{ MTTF =100\,\! }[/math] hours, or [math]\displaystyle{ \lambda =0.01\,\! }[/math], and with preventive replacement every 50 hours. Reliability vs. time for a single component with an [math]\displaystyle{ MTTF =100\,\! }[/math] hours, or [math]\displaystyle{ \lambda =0.01\,\! }[/math], and with preventive replacement every 50 hours.](/images/9/95/7i2.png)
However, consider the following cases for a single component:
Case 1: The component's reliability from 0 to 60 hours:
- With preventive maintenance, the component was replaced with a new one at 50 hours so the overall reliability is based on the reliability of the new component for 10 hours, [math]\displaystyle{ R(t=10)=90.48%\,\! }[/math], times the reliability of the previous component, [math]\displaystyle{ R(t=50)=60.65%\,\! }[/math]. The result is [math]\displaystyle{ R(t=60)=54.88%.\,\! }[/math]
- Without preventive maintenance, the reliability would be the reliability of the same component operating to 60 hours, or [math]\displaystyle{ R(t=60)=54.88%\,\! }[/math].
Case 2: The component's reliability from 50 to 60 hours:
- With preventive maintenance, the component was replaced at 50 hours, so this is solely based on the reliability of the new component for a mission of 10 hours, or [math]\displaystyle{ R(t=10)=90.48%\,\! }[/math].
- Without preventive maintenance, the reliability would be the conditional reliability of the same component operating to 60 hours, having already survived to 50 hours, or [math]\displaystyle{ {{R}_{C}}(t=10|T=50)=R(60)/R(50)=90.48%\,\! }[/math].
As can be seen, both cases — with and without preventive maintenance — yield the same results.
Determining Preventive Replacement Time
As mentioned earlier, if the component has an increasing failure rate, then a carefully designed preventive maintenance program is beneficial to system availability. Otherwise, the costs of preventive maintenance might actually outweigh the benefits. The objective of a good preventive maintenance program is to either minimize the overall costs (or downtime, etc.) or meet a reliability objective. In order to achieve this, an appropriate interval (time) for scheduled maintenance must be determined. One way to do that is to use the optimum age replacement model, as presented next. The model adheres to the conditions discussed previously:
- • The component is exhibiting behavior associated with a wear-out mode. That is, the failure rate of the component is increasing with time.
- • The cost for planned replacements is significantly less than the cost for unplanned replacements.
The following figure shows the Cost Per Unit Time vs. Time plot and it can be seen that the corrective replacement costs increase as the replacement interval increases. In other words, the less often you perform a PM action, the higher your corrective costs will be. Obviously, as we let a component operate for longer times, its failure rate increases to a point that it is more likely to fail, thus requiring more corrective actions. The opposite is true for the preventive replacement costs. The longer you wait to perform a PM, the less the costs; if you do PM too often, the costs increase. If we combine both costs, we can see that there is an optimum point that minimizes the costs. In other words, one must strike a balance between the risk (costs) associated with a failure while maximizing the time between PM actions.
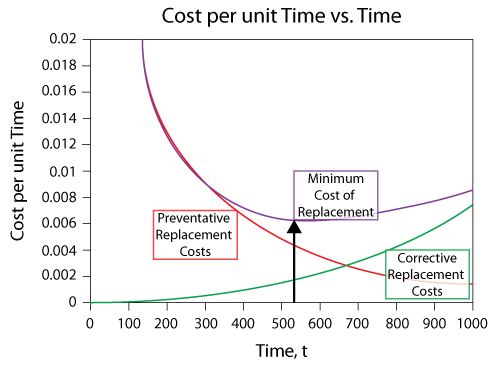
Optimum Age Replacement Policy
To determine the optimum time for such a preventive maintenance action (replacement), we need to mathematically formulate a model that describes the associated costs and risks. In developing the model, it is assumed that if the unit fails before time [math]\displaystyle{ t\,\! }[/math], a corrective action will occur and if it does not fail by time [math]\displaystyle{ t\,\! }[/math], a preventive action will occur. In other words, the unit is replaced upon failure or after a time of operation, [math]\displaystyle{ t\,\! }[/math], whichever occurs first. Thus, the optimum replacement time can be found by minimizing the cost per unit time, [math]\displaystyle{ CPUT\left( t \right).\,\! }[/math] [math]\displaystyle{ CPUT\left( t \right)\,\! }[/math] is given by:
- [math]\displaystyle{ \begin{align} CPUT\left( t \right)= & \frac{\text{Total Expected Replacement Cost per Cycle}}{\text{Expected Cycle Length}} \\ = & \frac{{{C}_{P}}\cdot R\left( t \right)+{{C}_{U}}\cdot \left[ 1-R\left( t \right) \right]}{\int_{0}^{t}R\left( s \right)ds} \end{align}\,\! }[/math]
where:
- [math]\displaystyle{ R(t)\,\! }[/math] = reliability at time [math]\displaystyle{ t\,\! }[/math].
- [math]\displaystyle{ {{C}_{P}}\,\! }[/math] = cost of planned replacement.
- [math]\displaystyle{ {{C}_{U}}\,\! }[/math] = cost of unplanned replacement.
- [math]\displaystyle{ R(t)\,\! }[/math] = reliability at time [math]\displaystyle{ t\,\! }[/math].
The optimum replacement time interval, [math]\displaystyle{ t\,\! }[/math], is the time that minimizes [math]\displaystyle{ CPUT\left( t \right).\,\! }[/math] This can be found by solving for [math]\displaystyle{ t\,\! }[/math] such that:
- [math]\displaystyle{ \frac{\partial \left[ CPUT(t) \right]}{\partial t}=0\,\! }[/math]
Or by solving for a [math]\displaystyle{ t\,\! }[/math] that satisfies the following equation:
- [math]\displaystyle{ \frac{\partial \left[ \tfrac{{{C}_{P}}\cdot R\left( t \right)+{{C}_{U}}\cdot \left[ 1-R\left( t \right) \right]}{\int_{0}^{t}R\left( s \right)ds} \right]}{\partial t}=0\,\! }[/math]
Interested readers can refer to Barlow and Hunter [2] for more details on this model.
In BlockSim (Version 8 and above), you can use the Optimum Replacement window to determine the optimum replacement time either for an individual block or for multiple blocks in a diagram simultaneously. When working with multiple blocks, the calculations can be for individual blocks or for one or more groups of blocks. For each item that is included in the optimization calculations, you will need to specify the cost for a planned replacement and the cost for an unplanned replacement. This is done by calculating the costs for replacement based on the item settings using equations or simulation and then, if desired, manually entering any additional costs for either type of replacement in the corresponding columns of the table.
The equations used to calculate the costs of planned and unplanned tasks for each item based on its associated URD are as follows:
- For the cost of planned tasks, here denoted as PM cost:
- [math]\displaystyle{ \begin{align} \text{PM Cost}= \left(\text{PM Down Time Rate}+ \text{Block Level Down Time Rate} \right) \cdot \left( \text{MTTPM}+\text{Pool Delay} +\text{Crew Delay} \right) \\ + \text{Crew Labor Rate} \cdot \text{MTTPM} + \text{Cost per PM} + \text{Cost per Pool} +\text{Cost per Crew} \end{align}\,\! }[/math]
- Only PM tasks based on item age or system age (fixed or dynamic intervals) are considered. If there is more than one PM task based on item age, only the first one is considered.
- For the cost of the unplanned task, here denoted as CM cost:
- [math]\displaystyle{ \begin{align} \text{CM Cost}= & \left(\text{CM Down Time Rate}+ \text{Block Level Down Time Rate} \right) \cdot \left( \text{MTTR}+\text{Pool Delay} +\text{Crew Delay} \right) \\ & + \text{Crew Labor Rate} \cdot \text{MTTR} + \text{Cost per CM} + \text{Cost per Pool} +\text{Cost per Crew} +\text{Block Level Cost per Failure} \end{align}\,\! }[/math]
When using simulation, for costs associated with planned replacements, all preventive tasks based on item age or system age (fixed or dynamic intervals) are considered. Because each item is simulated as a system (i.e., in isolation from any other item), tasks triggered in other ways are not considered.
Example: Optimum Replacement Time
The failure distribution of a component is described by a 2-parameter Weibull distribution with [math]\displaystyle{ \beta = 2.5\,\! }[/math] and [math]\displaystyle{ \eta = 1000\,\! }[/math] hours.
- The cost for a corrective replacement is $5.
- The cost for a preventive replacement is $1.
- The cost for a corrective replacement is $5.
Estimate the optimum replacement age in order to minimize these costs.
Solution
Prior to obtaining an optimum replacement interval for this component, the assumptions of the following equation must be checked.
- [math]\displaystyle{ \begin{align} CPUT\left( t \right)= & \frac{\text{Total Expected Replacement Cost per Cycle}}{\text{Expected Cycle Length}} \\ = & \frac{{{C}_{P}}\cdot R\left( t \right)+{{C}_{U}}\cdot \left[ 1-R\left( t \right) \right]}{\int_{0}^{t}R\left( s \right)ds} \end{align}\,\! }[/math]
The component has an increasing failure rate because it follows a Weibull distribution with [math]\displaystyle{ \beta \,\! }[/math] greater than 1. Note that if [math]\displaystyle{ \beta =1\,\! }[/math], then the component has a constant failure rate, but if [math]\displaystyle{ \beta \lt 1\,\! }[/math], then it has a decreasing failure rate. If either of these cases exist, then preventive replacement is unwise. Furthermore, the cost for preventive replacement is less than the corrective replacement cost. Thus, the conditions for the optimum age replacement policy have been met.
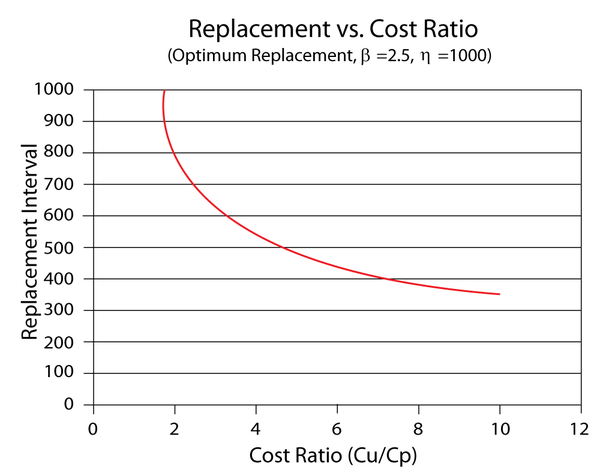
Using BlockSim, enter the parameters of the Weibull distribution in the component's Block Properties window. Next, open the Optimum Replacement window and enter the 1 in the Planned Replacement Cost column, and 5 in the Unplanned Replacement Cost column. Click Calculate. In the Optimum Replacement Calculations window that appears, select the Individual option and click OK. The optimum replacement time for the component is estimated to be 493.0470, as shown next.

The figure below shows the Cost vs. Time plot of the component (with the scaling adjusted and the plot annotated to show the minimum cost).
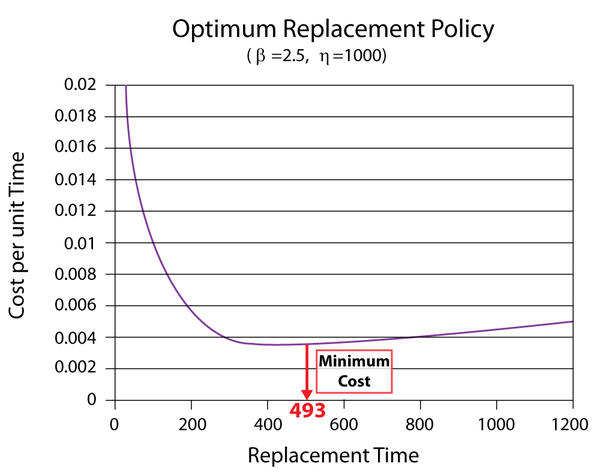
If we enter different cost values in the Unplanned Replacement Cost column and obtain the optimum replacement time at each value, we can use the data points to create a plot that shows the effect of the corrective cost on the optimum replacement interval. The following plot shows an example. In this case, the optimum replacement interval decreases as the cost ratio increases. This is an expected result because the corrective replacement costs are much greater than the preventive replacement costs. Therefore, it is more cost-effective to replace the component more frequently before it fails.