Parametric Binomial Example - Demonstrate MTTF: Difference between revisions
No edit summary |
Lisa Hacker (talk | contribs) No edit summary |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
<noinclude>{{Banner Weibull Examples}} | <noinclude>{{Banner Weibull Examples}} | ||
''This example appears in the [ | ''This example appears in the [https://help.reliasoft.com/reference/life_data_analysis Life data analysis reference]''. | ||
</noinclude> | </noinclude> | ||
In this example, we will use the parametric binomial method to design a test that will demonstrate | In this example, we will use the parametric binomial method to design a test that will demonstrate <math>MTTF=75\,\!</math> hours with a 95% confidence if no failure occur during the test <math>f=0\,\!</math>. We will assume a Weibull distribution with a shape parameter <math>\beta =1.5\,\!</math>. We want to determine the number of units to test for <math>{{t}_{TEST}}=60\,\!</math> hours to demonstrate this goal. | ||
The first step in this case involves determining the value of the scale parameter | The first step in this case involves determining the value of the scale parameter <math>\eta \,\!</math> from the <math>MTTF\,\!</math> equation. The equation for the <math>MTTF\,\!</math> for the Weibull distribution is: | ||
::<math>MTTF=\eta \cdot \Gamma (1+\frac{1}{\beta })</math> | ::<math>MTTF=\eta \cdot \Gamma (1+\frac{1}{\beta })\,\!</math> | ||
where | where <math>\Gamma (x)\,\!</math> is the gamma function of <math>x\,\!</math>. This can be rearranged in terms of <math>\eta\,\!</math>: | ||
::<math>\eta =\frac{MTTF}{\Gamma (1+\tfrac{1}{\beta })}</math> | ::<math>\eta =\frac{MTTF}{\Gamma (1+\tfrac{1}{\beta })}\,\!</math> | ||
Since | Since <math>MTTF\,\!</math> and <math>\beta \,\!</math> have been specified, it is a relatively simple matter to calculate <math>\eta =83.1\,\!</math>. From this point on, the procedure is the same as the reliability demonstration example. Next, the value of <math>{{R}_{TEST}}\,\!</math> is calculated as: | ||
::<math>{{R}_{TEST}}={{e}^{-{{({{t}_{TEST}}/\eta )}^{\beta }}}}={{e}^{-{{(60/83.1)}^{1.5}}}}=0.541=54.1%</math> | ::<math>{{R}_{TEST}}={{e}^{-{{({{t}_{TEST}}/\eta )}^{\beta }}}}={{e}^{-{{(60/83.1)}^{1.5}}}}=0.541=54.1%\,\!</math> | ||
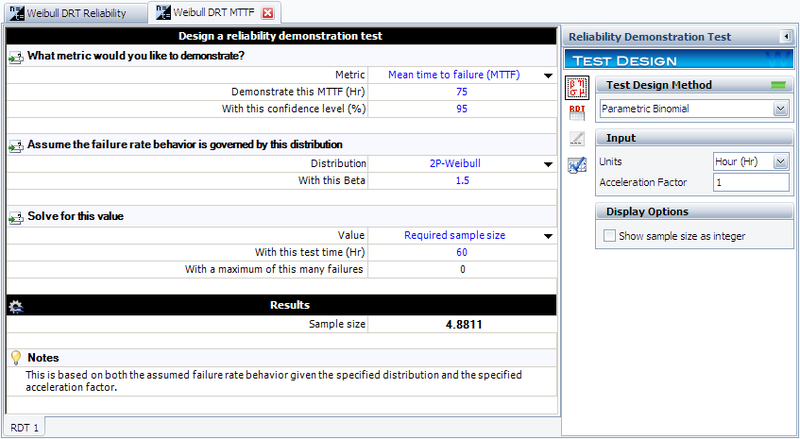
The last step is to substitute the appropriate values into the cumulative binomial equation. The values of | The last step is to substitute the appropriate values into the cumulative binomial equation. The values of <math>CL\,\!</math>, <math>{{t}_{TEST}}\,\!</math>, <math>\beta \,\!</math>, <math>f\,\!</math> and <math>\eta \,\!</math> have already been calculated or specified, so it merely remains to solve the binomial equation for <math>n\,\!</math>. The value is calculated as <math>n=4.8811,\,\!</math> or <math>n=5\,\!</math> units, since the fractional value must be rounded up to the next integer value. This example solved in Weibull++ is shown next. | ||
[[Image:RDT Weibull Demonstrate MTTF.png|center| | [[Image:RDT Weibull Demonstrate MTTF.png|center|800px| ]] | ||
The procedure for determining the required test time proceeds in the same manner, determining | The procedure for determining the required test time proceeds in the same manner, determining <math>\eta \,\!</math> from the <math>MTTF\,\!</math> equation, and following the previously described methodology to determine <math>{{t}_{TEST}}\,\!</math> from the binomial equation with Weibull distribution. | ||
Latest revision as of 18:55, 18 September 2023
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.
This example appears in the Life data analysis reference.
In this example, we will use the parametric binomial method to design a test that will demonstrate [math]\displaystyle{ MTTF=75\,\! }[/math] hours with a 95% confidence if no failure occur during the test [math]\displaystyle{ f=0\,\! }[/math]. We will assume a Weibull distribution with a shape parameter [math]\displaystyle{ \beta =1.5\,\! }[/math]. We want to determine the number of units to test for [math]\displaystyle{ {{t}_{TEST}}=60\,\! }[/math] hours to demonstrate this goal.
The first step in this case involves determining the value of the scale parameter [math]\displaystyle{ \eta \,\! }[/math] from the [math]\displaystyle{ MTTF\,\! }[/math] equation. The equation for the [math]\displaystyle{ MTTF\,\! }[/math] for the Weibull distribution is:
- [math]\displaystyle{ MTTF=\eta \cdot \Gamma (1+\frac{1}{\beta })\,\! }[/math]
where [math]\displaystyle{ \Gamma (x)\,\! }[/math] is the gamma function of [math]\displaystyle{ x\,\! }[/math]. This can be rearranged in terms of [math]\displaystyle{ \eta\,\! }[/math]:
- [math]\displaystyle{ \eta =\frac{MTTF}{\Gamma (1+\tfrac{1}{\beta })}\,\! }[/math]
Since [math]\displaystyle{ MTTF\,\! }[/math] and [math]\displaystyle{ \beta \,\! }[/math] have been specified, it is a relatively simple matter to calculate [math]\displaystyle{ \eta =83.1\,\! }[/math]. From this point on, the procedure is the same as the reliability demonstration example. Next, the value of [math]\displaystyle{ {{R}_{TEST}}\,\! }[/math] is calculated as:
- [math]\displaystyle{ {{R}_{TEST}}={{e}^{-{{({{t}_{TEST}}/\eta )}^{\beta }}}}={{e}^{-{{(60/83.1)}^{1.5}}}}=0.541=54.1%\,\! }[/math]
The last step is to substitute the appropriate values into the cumulative binomial equation. The values of [math]\displaystyle{ CL\,\! }[/math], [math]\displaystyle{ {{t}_{TEST}}\,\! }[/math], [math]\displaystyle{ \beta \,\! }[/math], [math]\displaystyle{ f\,\! }[/math] and [math]\displaystyle{ \eta \,\! }[/math] have already been calculated or specified, so it merely remains to solve the binomial equation for [math]\displaystyle{ n\,\! }[/math]. The value is calculated as [math]\displaystyle{ n=4.8811,\,\! }[/math] or [math]\displaystyle{ n=5\,\! }[/math] units, since the fractional value must be rounded up to the next integer value. This example solved in Weibull++ is shown next.
The procedure for determining the required test time proceeds in the same manner, determining [math]\displaystyle{ \eta \,\! }[/math] from the [math]\displaystyle{ MTTF\,\! }[/math] equation, and following the previously described methodology to determine [math]\displaystyle{ {{t}_{TEST}}\,\! }[/math] from the binomial equation with Weibull distribution.