Test-Fix-Find-Test Data Example: Difference between revisions
mNo edit summary |
Lisa Hacker (talk | contribs) No edit summary |
||
| Line 1: | Line 1: | ||
<noinclude>{{Banner RGA Examples}} | <noinclude>{{Banner RGA Examples}} | ||
''This example appears in the [ | ''This example appears in the [https://help.reliasoft.com/reference/reliability_growth_and_repairable_system_analysis Reliability growth reference]''. | ||
</noinclude> | </noinclude> | ||
Latest revision as of 21:23, 18 September 2023
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at RGA examples and RGA reference examples.
This example appears in the Reliability growth reference.
Consider the data given in the first table below. There were 56 total failures and [math]\displaystyle{ T=400\,\! }[/math]. The effectiveness factors of the unique BD modes are given in the second table. Determine the following:
- Calculate the demonstrated MTBF and failure intensity.
- Calculate the projected MTBF and failure intensity.
- What is the rate at which unique BD modes are being generated during this test?
- If the test continues for an additional 50 hours, what is the minimum number of new unique BD modes expected to be generated?
| Test-Fix-Find-Test Data | |||||
| [math]\displaystyle{ i\,\! }[/math] | [math]\displaystyle{ {{X}_{i}}\,\! }[/math] | Mode | [math]\displaystyle{ i\,\! }[/math] | [math]\displaystyle{ {{X}_{i}}\,\! }[/math] | Mode |
|---|---|---|---|---|---|
| 1 | 0.7 | BC17 | 29 | 192.7 | BD11 |
| 2 | 3.7 | BC17 | 30 | 213 | A |
| 3 | 13.2 | BC17 | 31 | 244.8 | A |
| 4 | 15 | BD1 | 32 | 249 | BD12 |
| 5 | 17.6 | BC18 | 33 | 250.8 | A |
| 6 | 25.3 | BD2 | 34 | 260.1 | BD1 |
| 7 | 47.5 | BD3 | 35 | 263.5 | BD8 |
| 8 | 54 | BD4 | 36 | 273.1 | A |
| 9 | 54.5 | BC19 | 37 | 274.7 | BD6 |
| 10 | 56.4 | BD5 | 38 | 282.8 | BC27 |
| 11 | 63.6 | A | 39 | 285 | BD13 |
| 12 | 72.2 | BD5 | 40 | 304 | BD9 |
| 13 | 99.2 | BC20 | 41 | 315.4 | BD4 |
| 14 | 99.6 | BD6 | 42 | 317.1 | A |
| 15 | 100.3 | BD7 | 43 | 320.6 | A |
| 16 | 102.5 | A | 44 | 324.5 | BD12 |
| 17 | 112 | BD8 | 45 | 324.9 | BD10 |
| 18 | 112.2 | BC21 | 46 | 342 | BD5 |
| 19 | 120.9 | BD2 | 47 | 350.2 | BD3 |
| 20 | 121.9 | BC22 | 48 | 355.2 | BC28 |
| 21 | 125.5 | BD9 | 49 | 364.6 | BD10 |
| 22 | 133.4 | BD10 | 50 | 364.9 | A |
| 23 | 151 | BC23 | 51 | 366.3 | BD2 |
| 24 | 163 | BC24 | 52 | 373 | BD8 |
| 25 | 164.7 | BD9 | 53 | 379.4 | BD14 |
| 26 | 174.5 | BC25 | 54 | 389 | BD15 |
| 27 | 177.4 | BD10 | 55 | 394.9 | A |
| 28 | 191.6 | BC26 | 56 | 395.2 | BD16 |
| Effectiveness Factors for the Unique BD Modes | |
| BD Mode | EF [math]\displaystyle{ {{d}_{i}}\,\! }[/math] |
|---|---|
| 1 | .67 |
| 2 | .72 |
| 3 | .77 |
| 4 | .77 |
| 5 | .87 |
| 6 | .92 |
| 7 | .50 |
| 8 | .85 |
| 9 | .89 |
| 10 | .74 |
| 11 | .70 |
| 12 | .63 |
| 13 | .64 |
| 14 | .72 |
| 15 | .69 |
| 16 | .46 |
Solution
- In order to obtain [math]\displaystyle{ {{\widehat{\lambda }}_{CA}}\,\! }[/math], use the traditional Crow-AMSAA model for test-fix-test to fit all 56 data points, regardless of the failure mode classification to get:
- [math]\displaystyle{ \begin{align} \widehat{\beta }= & 0.91026 \\ \widehat{\lambda }= & 0.23969 \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} {{\widehat{\lambda }}_{CA}} = & \widehat{\lambda }\widehat{\beta }{{T}^{\widehat{\beta }-1}} \\ = & 0.23969\times 0.91026\times {{400}^{(0.91026-1)}} \\ = & 0.12744 \end{align}\,\! }[/math]
- [math]\displaystyle{ {{\widehat{M}}_{CA}}={{[{{\widehat{\lambda }}_{CA}}]}^{-1}}=7.84708\,\! }[/math]
- For this data set, [math]\displaystyle{ M=16\,\! }[/math] and [math]\displaystyle{ T=400\,\! }[/math].
- [math]\displaystyle{ {{\widehat{\lambda }}_{BD}}=\frac{{{N}_{BD}}}{T}=\frac{32}{400}=0.08\,\! }[/math]
- [math]\displaystyle{ \overline{d}=\underset{i=1}{\overset{M}{\mathop \sum }}\,{{d}_{i}}/M=0.72125\,\! }[/math]
- [math]\displaystyle{ \underset{i=1}{\overset{16}{\mathop \sum }}\,(1-{{d}_{i}}){{N}_{i}}/T=0.01955\,\! }[/math]
- [math]\displaystyle{ \begin{align} {{{\hat{\beta }}}_{BD}}= & 0.74715 \\ {{{\hat{\lambda }}}_{BD}} = & 0.18197 \end{align}\,\! }[/math]
- [math]\displaystyle{ \overline{d}\widehat{h}(T|BD)=0.0215\,\! }[/math]
- [math]\displaystyle{ \begin{align} {{\widehat{\lambda }}_{EM}} = & {{\widehat{\lambda }}_{CA}}-{{\widehat{\lambda }}_{BD}}+\underset{i=1}{\overset{K}{\mathop \sum }}\,(1-{{d}_{i}})\frac{{{N}_{i}}}{T}+\overline{d}\widehat{h}(T|BD) \\ = & 0.12744-0.08+0.0196+0.0215 \\ = & 0.08854 \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} {{\widehat{M}}_{EM}} = & {{[{{\widehat{\lambda }}_{EM}}]}^{-1}} \\ = & 11.29418 \end{align}\,\! }[/math]
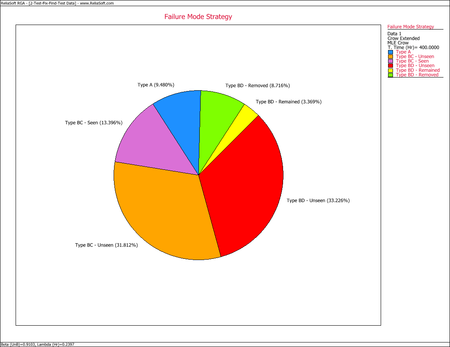
This pie chart shows that 9.48% of the system's failure intensity has been left in (A modes), 31.81% of the failure intensity due to the BC modes has not been seen yet and 13.40% was removed during the test (BC modes - seen). In addition, 33.23% of the failure intensity due to the BD modes has not been seen yet, 3.37% will remain in the system since the corrective actions will not be completely effective at eliminating the identified failure modes, and 8.72% will be removed after the delayed corrective actions.
- The rate at which unique BD modes are being generated is equal to [math]\displaystyle{ h{{(T|BD)}^{-1}}\,\! }[/math], where:
- [math]\displaystyle{ \begin{align} h{{(T|BD)}^{-1}} = & \frac{1}{{{\widehat{\lambda }}_{BD}}{{\widehat{\beta }}_{BD}}{{T}^{{{\widehat{\beta }}_{BD}}-1}}} \\ = & \frac{T}{M{{\widehat{\beta }}_{BD}}} \\ = & 33.4605 \end{align}\,\! }[/math]
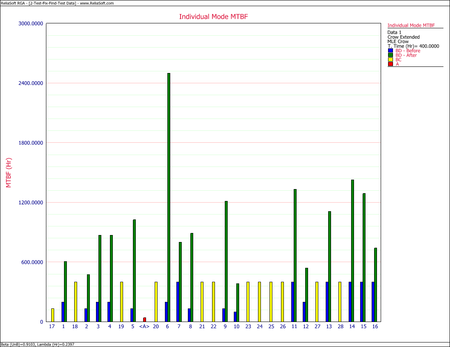
- Unique BD modes are being generated every 33.4605 hours. If the test continues for another 50 hours, then at least one new unique BD mode would be expected to be seen from this additional testing. As shown in the next figure, the MTBF of each individual failure mode can be plotted, and the failure modes with the lowest MTBF can be identified. These are the failure modes that cause the majority of the system failures.