Interval Data Example: Difference between revisions
Chris Kahn (talk | contribs) |
No edit summary |
||
| Line 2: | Line 2: | ||
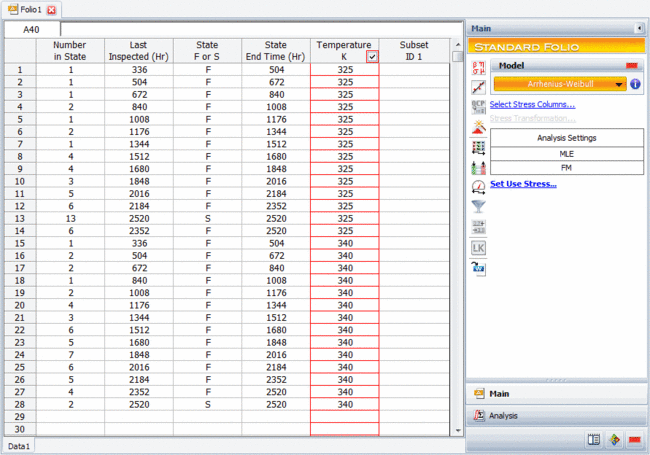
A sample of and electronic device was tested in two testing chambers set at different temperatures and monitored on a weekly basis. The test was performed continuously for 15 weeks. 50 units were put in each chamber. The goal of the test is to estimate the 90% lower bound on the <math>B10</math> life (in hours) of the electronic device. The following figure represents the test results, it shows the test results entered in ALTA in an interval data format. The normal use condition is assumed to be 300K. | A sample of and electronic device was tested in two testing chambers set at different temperatures and monitored on a weekly basis. The test was performed continuously for 15 weeks. 50 units were put in each chamber. The goal of the test is to estimate the 90% lower bound on the <math>B10</math> life (in hours) of the electronic device. The following figure represents the test results, it shows the test results entered in ALTA in an interval data format. The normal use condition is assumed to be 300K. | ||
[[Image:chapter14_80.gif|center|650px|]] | |||
[[Image:chapter14_80.gif | |||
====Solution==== | ====Solution==== | ||
Assuming that the failure times of the devices follow a Weibull distribution and that the Arrhenius model is an adequate life-stress relationship, we obtain the following estimated model parameters: | Assuming that the failure times of the devices follow a Weibull distribution and that the Arrhenius model is an adequate life-stress relationship, we obtain the following estimated model parameters: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
| Line 16: | Line 13: | ||
\end{align}</math> | \end{align}</math> | ||
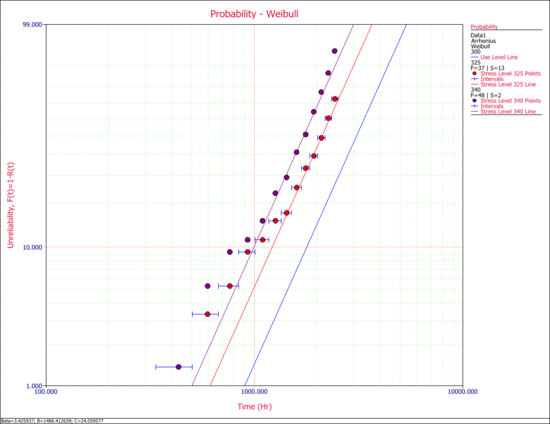
The next figure show the probability lines at the different stress levels along with the extrapolated use level probability line. | |||
[[Image:intervaldataproblines.gif|thumb|center|550px|Probability lines at the different test stress levels with the extrapolated use level probability line.]] | |||
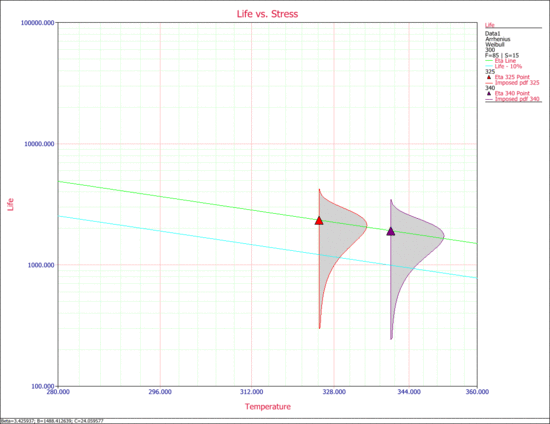
The following is the life versus stress plot showing the <math>B10</math> life line. | The following is the life versus stress plot showing the <math>B10</math> life line. | ||
[[Image:ch14-23.gif|thumb|center|550px|Life vs. Stress with the ''B''10 life line (bottom).]] | |||
[[Image:ch14-23.gif|thumb|center| | |||
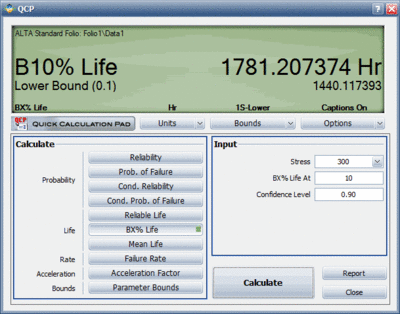
The 90% lower bound on the <math>B10</math> life can be estimated as follows. | The 90% lower bound on the <math>B10</math> life can be estimated as follows. | ||
[[Image:intervalb10qcp.gif|center|400px|]] | |||
[[Image:intervalb10qcp.gif | |||
Revision as of 06:54, 9 August 2012
Interval Data Example
A sample of and electronic device was tested in two testing chambers set at different temperatures and monitored on a weekly basis. The test was performed continuously for 15 weeks. 50 units were put in each chamber. The goal of the test is to estimate the 90% lower bound on the [math]\displaystyle{ B10 }[/math] life (in hours) of the electronic device. The following figure represents the test results, it shows the test results entered in ALTA in an interval data format. The normal use condition is assumed to be 300K.
Solution
Assuming that the failure times of the devices follow a Weibull distribution and that the Arrhenius model is an adequate life-stress relationship, we obtain the following estimated model parameters:
- [math]\displaystyle{ \begin{align} \beta =\ & 3.425937 \\ B=\ & 1488.412639 \\ C=\ & 24.059577 \end{align} }[/math]
The next figure show the probability lines at the different stress levels along with the extrapolated use level probability line.
The following is the life versus stress plot showing the [math]\displaystyle{ B10 }[/math] life line.
The 90% lower bound on the [math]\displaystyle{ B10 }[/math] life can be estimated as follows.