Template:Aaw stat prob sum
Arrhenius-Weibull Statistical Properties Summary
Mean or MTTF
The mean, [math]\displaystyle{ \overline{T} }[/math] (also called [math]\displaystyle{ MTTF }[/math] by some authors), of the Arrhenius-Weibull relationship is given by:
- [math]\displaystyle{ \overline{T}=C\cdot {{e}^{\tfrac{B}{V}}}\cdot \Gamma \left( \frac{1}{\beta }+1 \right) }[/math]
where [math]\displaystyle{ \Gamma \left( \tfrac{1}{\beta }+1 \right) }[/math] is the gamma function evaluated at the value of [math]\displaystyle{ \left( \tfrac{1}{\beta }+1 \right) }[/math] .
Median
The median, [math]\displaystyle{ \breve{T}, }[/math]
for the Arrhenius-Weibull model is given by:
- [math]\displaystyle{ \breve{T}=C\cdot {{e}^{\tfrac{B}{V}}}{{\left( \ln 2 \right)}^{\tfrac{1}{\beta }}} }[/math]
Mode
The mode, [math]\displaystyle{ \tilde{T}, }[/math]
for the Arrhenius-Weibull model is given by:
- [math]\displaystyle{ \tilde{T}=C\cdot {{e}^{\tfrac{B}{V}}}{{\left( 1-\frac{1}{\beta } \right)}^{\tfrac{1}{\beta }}} }[/math]
Standard Deviation
The standard deviation, [math]\displaystyle{ {{\sigma }_{T}}, }[/math] for the Arrhenius-Weibull model is given by:
- [math]\displaystyle{ {{\sigma }_{T}}=C\cdot {{e}^{\tfrac{B}{V}}}\cdot \sqrt{\Gamma \left( \frac{2}{\beta }+1 \right)-{{\left( \Gamma \left( \frac{1}{\beta }+1 \right) \right)}^{2}}} }[/math]
Arrhenius-Weibull Reliability Function
The Arrhenius-Weibull reliability function is given by:
- [math]\displaystyle{ R(T,V)={{e}^{-{{\left( \tfrac{T}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta }}}} }[/math]
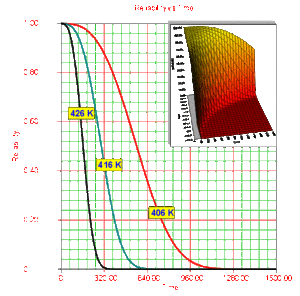
If the parameter [math]\displaystyle{ B }[/math] is positive, then the reliability increases as stress decreases.
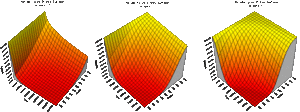
The behavior of the reliability function of the Weibull distribution for different values of [math]\displaystyle{ \beta }[/math] was illustrated in Chapter 5. In the case of the Arrhenius-Weibull model, however, the reliability is a function of stress also. A 3D plot such as the ones shown in Fig. 8 is now needed to illustrate the effects of both the stress and [math]\displaystyle{ \beta . }[/math]
- [math]\displaystyle{ }[/math]
Conditional Reliability Function
The Arrhenius-Weibull conditional reliability function at a specified stress level is given by:
- [math]\displaystyle{ R(T,t,V)=\frac{R(T+t,V)}{R(T,V)}=\frac{{{e}^{-{{\left( \tfrac{T+t}{\eta } \right)}^{\beta }}}}}{{{e}^{-{{\left( \tfrac{T}{\eta } \right)}^{\beta }}}}} }[/math]
or:
- [math]\displaystyle{ R(T,t,V)={{e}^{-\left[ {{\left( \tfrac{T+t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta }}-{{\left( \tfrac{T}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta }} \right]}} }[/math]
Reliable Life
For the Arrhenius-Weibull relationship, the reliable life, [math]\displaystyle{ {{t}_{R}} }[/math] , of a unit for a specified reliability and starting the mission at age zero is given by:
- [math]\displaystyle{ {{t}_{R}}=C\cdot {{e}^{\tfrac{B}{V}}}{{\left\{ -\ln \left[ R\left( {{t}_{R}},V \right) \right] \right\}}^{\tfrac{1}{\beta }}} }[/math]
This is the life for which the unit will function successfully with a reliability of [math]\displaystyle{ R({{t}_{R}}) }[/math] . If [math]\displaystyle{ R({{t}_{R}})=0.50 }[/math] then [math]\displaystyle{ {\breve{T} }[/math],
the median life, or the life by which half of the units will survive.
Arrhenius-Weibull Failure Rate Function
The Arrhenius-Weibull failure rate function, [math]\displaystyle{ \lambda (T) }[/math] , is given by:
- [math]\displaystyle{ \lambda \left( T,V \right)=\frac{f\left( T,V \right)}{R\left( T,V \right)}=\frac{\beta }{C\cdot {{e}^{\tfrac{B}{V}}}}{{\left( \frac{T}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta -1}} }[/math]