Stress-Strength Analysis in Design for Reliability
Using Stress-Strength Analysis to Determine the Required Strength Distribution
Assume the stress distribution for a component is known and it is a Weibull distribution with beta=3 and eta=2000. For the current design, the strength distribution is also a Weibull distribution with beta =1.5 and eta=4000.
- • Evaluate the current reliability.
- • If the reliability does not meet the target reliability of 90%, determine what parameters would be required for the strength distribution in order to meet the specified target.
Solution
First, we need to create two empty Weibull++ standard folios and enter the distribution parameters for the stress and strength distributions. For example, for the stress distribution, it is:
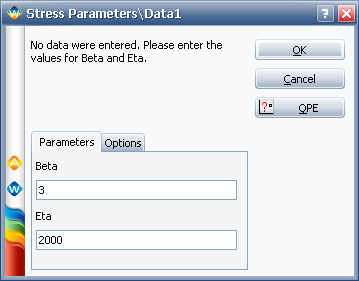
Then, following the steps given in Example 1, the reliability of the current design is given in the following figure:
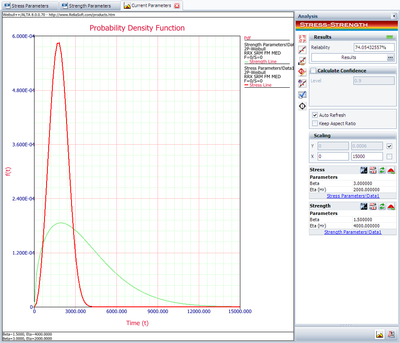
The above result shows that the current reliability is about 74.05%, which is below the target value of 90%. We need to use the Target Reliability Parameter Estimator to determine the parameter for the strength distribution that would be required to meet the target. Click on the following icon:

Choose to calculate for eta under Strength Parameters, set the Target Reliability to 90%, and click Calculate:
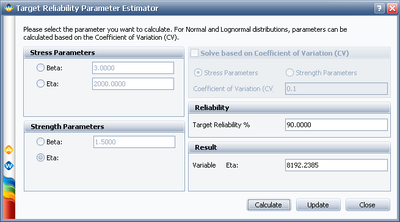
The calculated eta is 8192.2385 hours. Click Update to perform the stress-strength analysis again using the altered parameters for the strength distribution.
The plot shows the calculated reliability indeed is 90%.
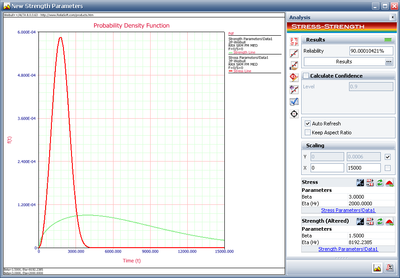
Therefore, in order to meet the reliability requirement, the component must be redesigned with the eta to be at least 8192.2385 hours.