Template:Confidence bounds lloyd-l

Confidence Bounds

In this section, the methods used in RGA to estimate the confidence bounds under the Lloyd-Lipow model will be presented. One of the properties of maximum likelihood estimators is that they are asymptotically normal. This indicates that they are normally distributed for large samples [6][7]. Additionally, since the parameter [math]\displaystyle{ \alpha }[/math] must be positive, [math]\displaystyle{ \ln \alpha }[/math] is treated as being normally distributed as well. The parameter [math]\displaystyle{ {{R}_{\infty }} }[/math] represents the ultimate reliability that would be attained if [math]\displaystyle{ k\to \infty }[/math] . [math]\displaystyle{ {{R}_{k}} }[/math] is the actual reliability during the [math]\displaystyle{ {{k}^{th}} }[/math] stage of testing. Therefore, [math]\displaystyle{ {{R}_{\infty }} }[/math] and [math]\displaystyle{ {{R}_{k}} }[/math] will be between 0 and 1. Consequently, the endpoints of the confidence intervals of the parameters [math]\displaystyle{ {{R}_{\infty }} }[/math] and [math]\displaystyle{ {{R}_{k}} }[/math] also will be between 0 and 1. To obtain the confidence interval, it is common practice to use the logit transformation. The confidence bounds on the parameters [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ {{R}_{\infty }} }[/math] are given by:

[math]\displaystyle{ C{{B}_{\alpha }}=\hat{\alpha }{{e}^{\pm {{z}_{\alpha /2}}\sqrt{Var(\hat{\alpha })}/\hat{\alpha }}} }[/math]

[math]\displaystyle{ C{{B}_{{{R}_{\infty }}}}=\frac{{{{\hat{R}}}_{\infty }}}{{{{\hat{R}}}_{\infty }}+(1-{{{\hat{R}}}_{\infty }}){{e}^{\pm {{z}_{\alpha /2}}\sqrt{Var({{{\hat{R}}}_{\infty }})}/\left[ {{{\hat{R}}}_{\infty }}(1-{{{\hat{R}}}_{\infty }}) \right]}}} }[/math]

where [math]\displaystyle{ {{z}_{\alpha /2}} }[/math] represents the percentage points of the [math]\displaystyle{ N(0,1) }[/math] distribution such that [math]\displaystyle{ P\{z\ge {{z}_{\alpha /2}}\}=\alpha /2 }[/math] . The confidence bounds on reliability are given by:

[math]\displaystyle{ CB=\frac{{{{\hat{R}}}_{k}}}{{{{\hat{R}}}_{k}}+(1-{{{\hat{R}}}_{k}}){{e}^{\pm {{z}_{\alpha /2}}\sqrt{Var({{{\hat{R}}}_{k}})}/\left[ {{{\hat{R}}}_{k}}(1-{{{\hat{R}}}_{k}}) \right]}}} }[/math]

where:

[math]\displaystyle{ Var({{\widehat{R}}_{k}})=Var({{\widehat{R}}_{\infty }})+\frac{1}{{{k}^{2}}}\cdot Var(\widehat{\alpha })-\frac{2}{k}\cdot Cov({{\widehat{R}}_{\infty }},\widehat{\alpha }) }[/math]

All the variances can be calculated using the Fisher Matrix:

[math]\displaystyle{ {{\left[ \begin{matrix} -\tfrac{{{\partial }^{2}}\Lambda }{\partial R_{\infty }^{2}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \alpha \partial {{R}_{\infty }}} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial \alpha \partial {{R}_{\infty }}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\alpha }^{2}}} \\ \end{matrix} \right]}^{-1}}=\left[ \begin{matrix} Var({{\widehat{R}}_{\infty }}) & Cov({{\widehat{R}}_{\infty }},\widehat{\alpha }) \\ Cov({{\widehat{R}}_{\infty }},\widehat{\alpha }) & Var(\widehat{\alpha }) \\ \end{matrix} \right] }[/math]

From Eqns. (R2) and (alpha2), taking the second partial derivatives yields:

[math]\displaystyle{ \frac{{{\partial }^{2}}\Lambda }{\partial R_{\infty }^{2}}=-\underset{k=1}{\overset{N}{\mathop \sum }}\,\frac{{{S}_{k}}}{{{\left( {{R}_{\infty }}-\tfrac{\alpha }{k} \right)}^{2}}}-\underset{k=1}{\overset{N}{\mathop \sum }}\,\frac{{{n}_{k}}-{{S}_{k}}}{{{\left( 1-{{R}_{\infty }}+\tfrac{\alpha }{k} \right)}^{2}}} }[/math]

[math]\displaystyle{ \frac{{{\partial }^{2}}\Lambda }{\partial {{\alpha }^{2}}}=-\underset{k=1}{\overset{N}{\mathop \sum }}\,\frac{\tfrac{{{S}_{k}}}{{{k}^{2}}}}{{{\left( {{R}_{\infty }}-\tfrac{\alpha }{k} \right)}^{2}}}-\underset{k=1}{\overset{N}{\mathop \sum }}\,\frac{\tfrac{{{n}_{k}}-{{S}_{k}}}{{{k}^{2}}}}{{{\left( 1-{{R}_{\infty }}+\tfrac{\alpha }{k} \right)}^{2}}} }[/math]

and:

[math]\displaystyle{ \frac{{{\partial }^{2}}\Lambda }{\partial {{R}_{\infty }}\partial \alpha }=\underset{k=1}{\overset{N}{\mathop \sum }}\,\frac{\tfrac{{{S}_{k}}}{k}}{{{\left( {{R}_{\infty }}-\tfrac{\alpha }{k} \right)}^{2}}}-\underset{k=1}{\overset{N}{\mathop \sum }}\,\frac{\tfrac{{{n}_{k}}-{{S}_{k}}}{k}}{{{\left( 1-{{R}_{\infty }}+\tfrac{\alpha }{k} \right)}^{2}}} }[/math]

Now the confidence bounds can be obtained after calculating Eqns. (cbll2) through (cbll5) and substituting into the Fisher Matrix.


Example 2
Plot the confidence bounds for the data in Table 6.1.


Solution
From Eqns. (cbll3), (cbll4) and (cbll5):

[math]\displaystyle{ \begin{align} & \frac{{{\partial }^{2}}\Lambda }{\partial R_{\infty }^{2}}= & -255.3835-937.2902=-1192.6737 \\ & \frac{{{\partial }^{2}}\Lambda }{\partial {{\alpha }^{2}}}= & -24.4575-43.3930=-67.8505 \\ & \frac{{{\partial }^{2}}\Lambda }{\partial {{R}_{\infty }}\partial \alpha }= & 48.6606-140.7518=-92.0912 \end{align} }[/math]

The variances can be calculated using the Fisher Matrix:

[math]\displaystyle{ \begin{align} & {{\left[ \begin{matrix} 1192.6737 & 92.0912 \\ 92.0912 & 67.8505 \\ \end{matrix} \right]}^{-1}}= & \left[ \begin{matrix} Var({{\widehat{R}}_{\infty }}) & Cov({{\widehat{R}}_{\infty }},\widehat{\alpha }) \\ Cov({{\widehat{R}}_{\infty }},\widehat{\alpha }) & Var(\widehat{\alpha }) \\ \end{matrix} \right] \\ & = & \left[ \begin{matrix} 0.00093661 & -0.00127123 \\ -0.00127123 & 0.01646371 \\ \end{matrix} \right] \end{align} }[/math]

Predicted reliability with 90% confidence bounds.

The variance of [math]\displaystyle{ {{R}_{k}} }[/math] is obtained from Eqn. (cbll2) such that:

[math]\displaystyle{ Var({{\widehat{R}}_{k}})=0.00093661+\frac{1}{{{k}^{2}}}\cdot 0.01646371+\frac{2}{k}\cdot 0.00127123 }[/math]

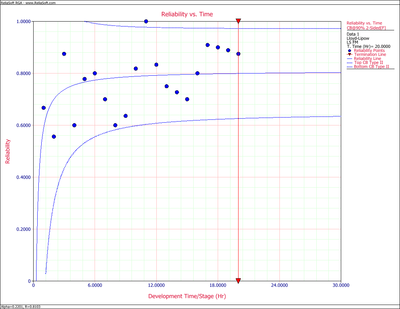
Now Eqn. (llrc) can be calculated and the associated confidence bounds at the [math]\displaystyle{ 90% }[/math] confidence level are plotted in Figure llfig62 with the predicted reliability, [math]\displaystyle{ {{R}_{k}} }[/math] .


Example 3
Consider the success/failure data given in Table 6.2. Solve for the Lloyd-Lipow parameters using least squares analysis and plot the Lloyd-Lipow reliability with 2-sided confidence bounds at the 90% confidence level.

Table 6.2 - Success/failure data for a variable number of tests performed in each test stage

Test Stage Number([math]\displaystyle{ k }[/math])	Result	Number of Tests([math]\displaystyle{ n_k }[/math]>	Successful Tests([math]\displaystyle{ S_k=R_i }[/math])
1	F	1	0
2	F	1	0
3	F	1	0
4	S	1	0.2500
5	F	1	0.2000
6	F	1	0.1667
7	S	1	0.2857
8	S	1	0.3750
9	S	1	0.4444
10	S	1	0.5000
11	S	1	0.5455
12	S	1	0.5833
13	S	1	0.6154
14	S	1	0.6429
15	S	1	0.6667
16	S	1	0.6875
17	F	1	0.6471
18	S	1	0.6667
19	F	1	0.6316
20	S	1	0.6500
21	S	1	0.6667
22	S	1	0.6818

Solution
Note that the data set contains three consecutive failures at the beginning of the test. These failures will be ignored throughout the analysis because it is considered that the test starts when the reliability is not equal to zero or one. The number of data points is now reduced to 19. Also note that the only time that the first three first failures are considered is to calculate the observed reliability in the test. For example, given this data set, the observed reliability at stage 4 is [math]\displaystyle{ 1/4=0.25 }[/math] . This is considered to be the reliability at stage 1.
From Table 6.2, the least squares estimates can be calculated as follows:

[math]\displaystyle{ \begin{align} & \underset{k=1}{\overset{N}{\mathop \sum }}\,\frac{1}{k}= & \underset{k=1}{\overset{19}{\mathop \sum }}\,\frac{1}{k}=3.54774 \\ & \underset{k=1}{\overset{N}{\mathop \sum }}\,\frac{1}{{{k}^{2}}}= & \underset{k=1}{\overset{19}{\mathop \sum }}\,\frac{1}{{{k}^{2}}}=1.5936 \\ & \underset{k=1}{\overset{N}{\mathop \sum }}\,\frac{{{S}_{k}}}{{{n}_{k}}}= & \underset{k=1}{\overset{19}{\mathop \sum }}\,\frac{{{S}_{k}}}{{{n}_{k}}}=9.907 \end{align} }[/math]

and:

[math]\displaystyle{ \underset{k=1}{\overset{N}{\mathop \sum }}\,\frac{{{S}_{k}}}{k\cdot {{n}_{k}}}=\underset{k=1}{\overset{19}{\mathop \sum }}\,\frac{{{S}_{k}}}{k\cdot {{n}_{k}}}=1.3002 }[/math]

Substituting into Eqns. (ar) and (alph) yields:

[math]\displaystyle{ \begin{align} & {{{\hat{R}}}_{\infty }}= & \frac{(1.5936)(9.907)-(3.5477)(1.3002)}{(19)(1.5936)-{{(3.5477)}^{2}}} \\ & = & 0.6316 \end{align} }[/math]

and:

[math]\displaystyle{ \begin{align} & \hat{\alpha }= & \frac{(3.5477)(9.907)-(19)(1.3002)}{(19)(1.5936)-{{(3.5477)}^{2}}} \\ & = & 0.5902 \end{align} }[/math]

Therefore, the Lloyd-Lipow reliability growth model is as follows, where [math]\displaystyle{ k }[/math] is the number of the test stage.

[math]\displaystyle{ {{R}_{k}}=0.6316-\frac{0.5902}{k} }[/math]

From Eqns. (cbll3), (cbll4), (cbll5) and the data given in Table 6.2:

[math]\displaystyle{ \begin{align} & \frac{{{\partial }^{2}}\Lambda }{\partial R_{\infty }^{2}}= & -176.847-40.500=-217.347 \\ & \frac{{{\partial }^{2}}\Lambda }{\partial {{\alpha }^{2}}}= & -146.763-2.1274=-148.891 \\ & \frac{{{\partial }^{2}}\Lambda }{\partial {{R}_{\infty }}\partial \alpha }= & 149.909-6.5660=143.343 \end{align} }[/math]

The variances can be calculated using the Fisher Matrix:

[math]\displaystyle{ \begin{align} & {{\left[ \begin{matrix} 217.347 & -143.343 \\ -143.343 & 148.891 \\ \end{matrix} \right]}^{-1}}= & \left[ \begin{matrix} Var({{\widehat{R}}_{\infty }}) & Cov({{\widehat{R}}_{\infty }},\widehat{\alpha }) \\ Cov({{\widehat{R}}_{\infty }},\widehat{\alpha }) & Var(\widehat{\alpha }) \\ \end{matrix} \right] \\ & = & \left[ \begin{matrix} 0.0126033 & 0.0121335 \\ 0.0121335 & 0.0183977 \\ \end{matrix} \right] \end{align} }[/math]

The variance of [math]\displaystyle{ {{R}_{k}} }[/math] is obtained from Eqn. (cbll2):

[math]\displaystyle{ Var({{\widehat{R}}_{k}})=0.0126031+\frac{1}{{{k}^{2}}}\cdot 0.0183977-\frac{2}{k}\cdot 0.0121335 }[/math]

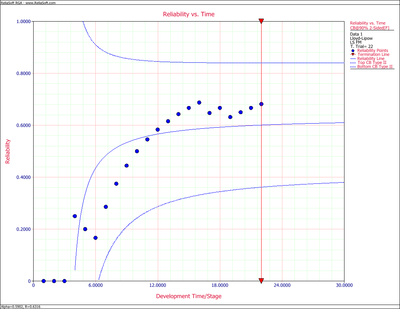
Now Eqn. (llrc) can be calculated and the associated confidence bounds on reliability at the [math]\displaystyle{ 90% }[/math] confidence level are plotted in Figure llfig63 with the predicted reliability, [math]\displaystyle{ {{R}_{k}} }[/math] .

Reliability vs. Time Plot with 90% confidence bounds.