1P-Exponential MLE Solution with Right Censored Data

From ReliaWiki
Revision as of 16:17, 28 September 2015 by Kate Racaza (talk | contribs)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Jump to navigation Jump to search
Weibull Reference Examples Banner.png


1P-Exponential MLE Solution with Right Censored Data

This example validates the calculations for the MLE solution and Fisher Matrix bound for a 1-parameter exponential distribution with right censored and complete failure data in Weibull++ standard folios.


Reference Case

The formulas on page 166 in the book Statistical Methods for Reliability Data by Dr. Meeker and Dr. Escobar, John Wiley & Sons, 1998.

[math]\hat{\theta}=\frac{TTT}{r}\ \ and\ \ se_{\hat{\theta}} = \frac{\hat{\theta}}{\sqrt{r}}\,\![/math]


where TTT is the total test time and r is the number of failures.


Data

Number in State State F or S Time to Failure
1 F 16
1 F 34
1 F 53
1 F 75
1 F 93
1 F 120
4 S 200


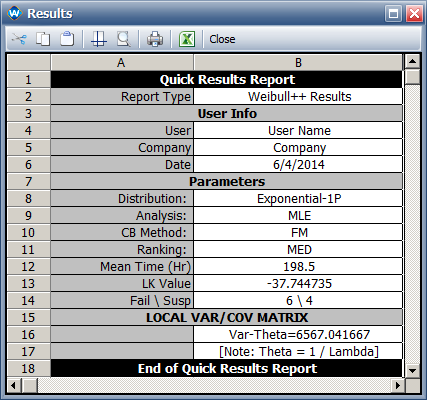
Result

[math]\begin{align} \hat{\theta} =& \frac{TTT}{r} = \frac{16+34+53+75+93+120+4\times 200}{6} = \frac{1191}{6} = 198.5 \\ \\ se_{\hat{\theta}} =& \frac{\theta}{\sqrt{r}} = \frac{198.5}{\sqrt{6}} = 81.037 \\ \end{align}\,\![/math]


So the variance of [math] \hat{\theta}\,\! [/math] is 6567.04


Results in Weibull++


1PE rcensored data.png
Retrieved from "https://www.reliawiki.com/index.php?title=1P-Exponential_MLE_Solution_with_Right_Censored_Data&oldid=60809"