Availability Analysis Reference Example
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at BlockSim examples and BlockSim reference examples.
|
Availability Analysis Reference Example |
This example validates the results for availability analysis BlockSim.
Reference Case
The data set is from example 11.3 on page 259 in the book, An Introduction to Reliability and Maintainability Engineering, by Dr. Charles E. Ebeling, McGraw-Hill, 1997.
Data
A two-component system’s point and interval availability for a 10 hour mission, and the steady-state availability for both series and parallel configurations are calculated. The components share the same failure rate and repair rate distributions. The failure and repair rates both follow exponential distributions with a failure rate of 0.1 failures per hour and a repair rate of 0.2 repairs per hour.
| Components of the System | Number of Failures, [math]\displaystyle{ \lambda_{f} }[/math] (per hour) |
Number of Repairs, [math]\displaystyle{ \lambda_{r} }[/math] (per hour) |
|---|---|---|
| Component 1 | 0.1 | 0.2 |
| Component 2 | 0.1 | 0.2 |
Result
The point availability is formulated in Equation 11.12 on page 257 in the reference book as:
- [math]\displaystyle{ P_{1}(t) = \frac{r}{\lambda + r} + \frac{\lambda}{\lambda + r}e^{-(\lambda+r)t}\,\! }[/math]
The interval availability is formulated in Equation 11.13 on page 258 in the reference book as:
- [math]\displaystyle{ A_{t2-t1} = \frac{r}{\lambda+r} + \frac{\lambda}{(\lambda+r)^{2}(t_{2}-t_{1})}\left [e^{-(\lambda+r)t_{1}} - e^{-(\lambda+r)t_{2}} \right ]\,\! }[/math]
The system availability for n independent components in series, each having a component availability of [math]\displaystyle{ A_{i}(t)\,\! }[/math], is given in Equation 11.15 on page 259 in the reference book as:
- [math]\displaystyle{ A_{s}(t) = \prod _{i=1}^{n}A_{i}(t)\,\! }[/math]
The system availability for n independent components in parallel, each having a component availability of [math]\displaystyle{ A_{i}(t)\,\! }[/math], is given in Equation 11.16 on page 259 in the reference book as:
- [math]\displaystyle{ A_{s}(t) = 1- \prod _{i=1}^{n}(1-A_{i}(t))\,\! }[/math]
Plugging in the numbers to the given equations, the point and interval availability for a 10 hour mission, and steady-state availability are calculated below.
For a series configuration:
- [math]\displaystyle{ \begin{align} A_{s}(10) = (0.684)^{2} = 0.468\\ A_{s,0-10} = (0.772)^{2} = 0.596\\ A_{s} = (0.667)^{2} = 0.445\\ \end{align}\,\! }[/math]
And for a parallel configuration:
- [math]\displaystyle{ \begin{align} A_{s}(10) = 1- (1- 0.684)^{2} = 0.900\\ A_{s,0-10} = 1- (1- 0.772)^{2} = 0.948\\ A_{s} = 1- (1- 0.667)^{2} = 0.889\\ \end{align}\,\! }[/math]
Results in BlockSim
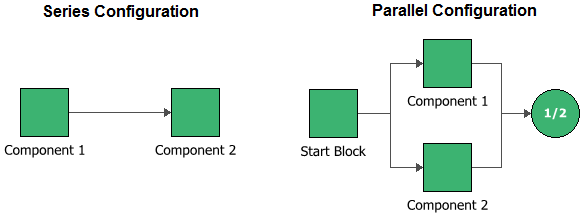
In BlockSim, the system RBDs are configured as shown below for series and parallel configurations. Since this is an availability example, we will validate the results via simulation.
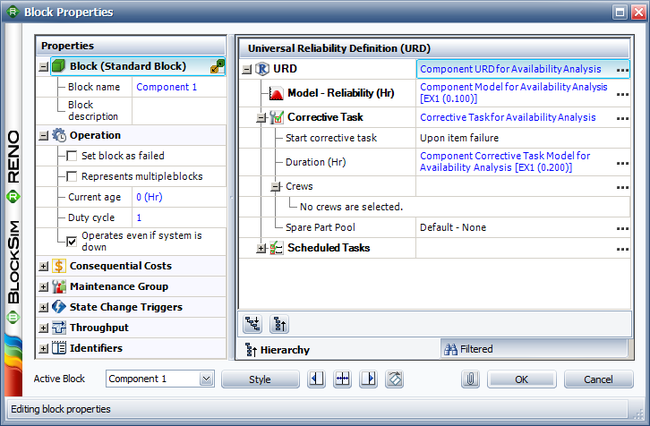
Each component is modeled using a 1-parameter exponential distribution with the given lambda (failure rate) values. They also share a corrective task that is modeled using a 1-parameter exponential distribution with the given lambda (repair rate) values. In this example, we are assuming that the component is fixed upon item failure to as good as new condition. One important point to keep in mind is that the component that is not failed still accumulates time while the corrective task is taking place for the component that failed. The reference book follows this assumption while driving the equations given above.
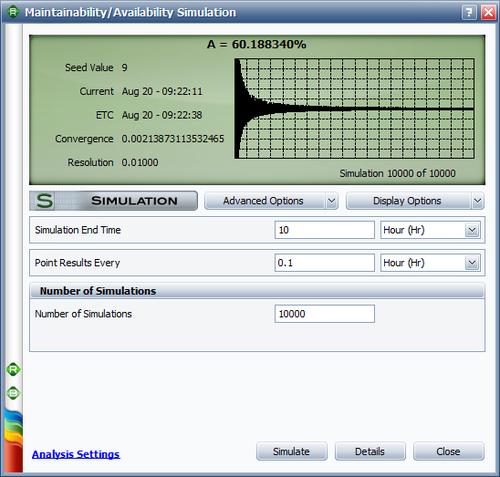
The same simulation setup is used for both series and parallel configurations. To estimate the point and interval availability for a 10 hour mission, we use a simulation end time of 10 hours. The settings are shown next.
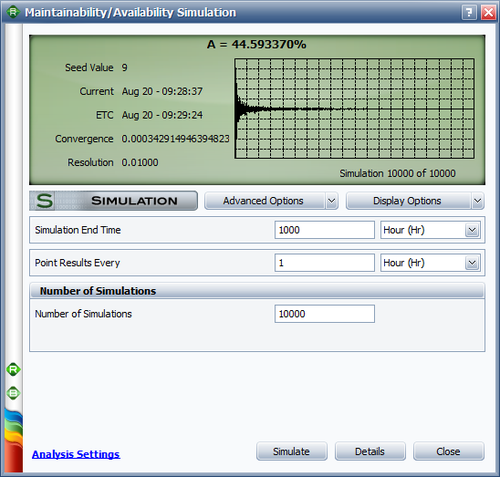
To estimate the steady-state availability, we use a simulation end time of 1,000 hours, since the system is assumed to reach steady state at that time. The settings are shown next.
The results of the BlockSim simulations for each configuration are given below. The numbers match with the results calculated in the reference book.
For series configuration:
- [math]\displaystyle{ \begin{align} A_{s}(10) &= 0.468\\ A_{s,0-10} &= 0.6019\\ A_{s} &= 0.4459\\ \end{align}\,\! }[/math]
And for parallel configuration:
- [math]\displaystyle{ \begin{align} A_{s}(10) &= 0.9000\\ A_{s,0-10} &= 0.9419\\ A_{s} &= 0.8893\\ \end{align}\,\! }[/math]