Component Importance Reference Example
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at BlockSim examples and BlockSim reference examples.
|
Component Importance Reference Example |
This example validates the component importance results for BlockSim diagrams.
Reference Case
The data set is from example 4.14 on page 100 in the book Life Cycle Reliability Engineering by Dr. Guangbin Yang, John Wiley & Sons, 2007.
Data
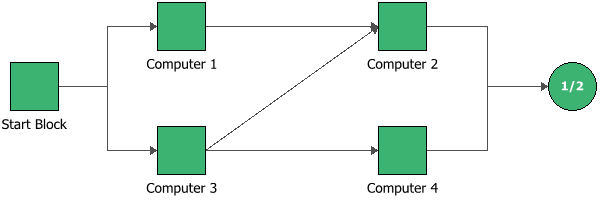
A computing system with four computers is configured as given in the BlockSim flowchart diagram below. (Please see Figure 4.29 on page 100 in the reference book for the original configuration.) Each computer follows an exponentially distributed failure rate with the given failure rate parameters in the table below. The Birnbaum’s importance measures of each computer in the system at 4000 and 8000 hours of operation are sought in this example. The system reliability equation, the reliabilities of each computer at the given times and the reliability importance at different times are also scrutinized.
| Computers of the Computing System | Number of Failures, [math]\displaystyle{ \lambda }[/math] (per hour) |
|---|---|
| Computer 1 | 5.5 x 10-6 |
| Computer 2 | 6.5 x 10-5 |
| Computer 3 | 4.3 x 10-5 |
| Computer4 | 7.3 x 10-6 |
Result
The system reliability equation is computed from Equation 4.40 on page 87 as:
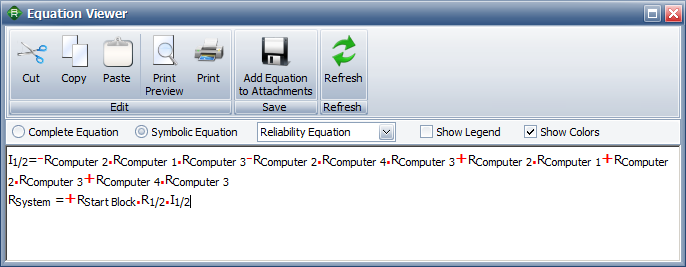
- [math]\displaystyle{ \begin{align} R&=Pr(system good|A)Pr(A)+Pr(system good|\bar{A})Pr(\bar{A})\\ R(t)&=[1-(1-R_{C1})(1-R_{C3})]R_{C2}+R_{C3}R_{C4}(1-R_{C2})\\ R(t)&=R_{C1}R_{C2}+R_{C2}R_{C3}+R_{C3}R_{C4}-R_{C1}R_{C2}R_{C3}-R_{C2}R_{C3}R_{C4}\\ \end{align}\,\! }[/math]
Since the times to failure of the computers are exponentially distributed and the reliability can be calculated via [math]\displaystyle{ R_{i} (t)=e^{-\lambda_{i} t}\,\! }[/math] for i = C1, C2, C3, and C4, the reliabilities of each computer at 4000 and 8000 hours are calculated as:
- [math]\displaystyle{ \begin{align} R_{C1}(4000)&=0.9782; R_{C2}(4000) = 0.7711\\ R_{C3}(4000)&=0.8420; R_{C2}(4000) = 0.9712\\ \end{align}\,\! }[/math]
and
- [math]\displaystyle{ \begin{align} R_{C1}(8000)&=0.9570; R_{C2}(8000) = 0.5945\\ R_{C3}(8000)&=0.7089; R_{C2}(8000) = 0.9433\\ \end{align}\,\! }[/math]
The system reliabilities at the specified times are calculated as:
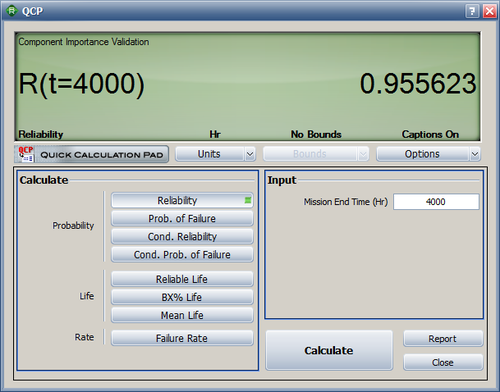
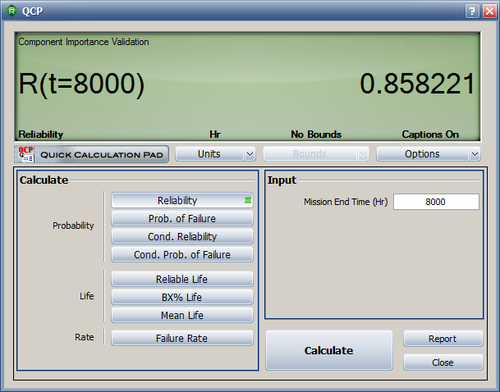
- [math]\displaystyle{ R(4000)=0.9556; R(8000) = 0.8582\,\! }[/math]
Birnbaum’s importance measures for each computer can be formulated via Equation 4.59 on page 100 as:
- [math]\displaystyle{ I_{B}(i|t)= \frac{\partial R(t)}{\partial R_{i}(t)}\,\! }[/math]
- [math]\displaystyle{ I_{B}(C1|t)= R_{2}(1-R_{3}); I_{B}(C2|t) = R_{1}+R_{3}-R_{1}R_{3}-R_{3}R_{4}\,\! }[/math]
- [math]\displaystyle{ I_{B}(C3|t)= R_{2}+ R_{4}- R_{1}R_{2} - R_{2}R_{4}; I_{B}(C4|t) = R_{3}(1 - R_{2})\,\! }[/math]
Therefore, the values of the importance measures can be calculated at 4000 and 8000 hours of operation as:
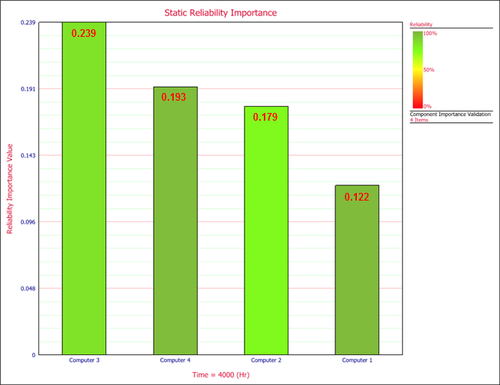
- [math]\displaystyle{ \begin{align} I_{B}(C1|4000)&= 0.1218; I_{B}(C2|4000)= 0.1788\\ I_{B}(C3|4000)&= 0.2391; I_{B}(C4|4000)= 0.1928\\ \end{align}\,\! }[/math]
and
- [math]\displaystyle{ \begin{align} I_{B}(C1|8000)&= 0.1730; I_{B}(C2|8000)= 0.3188\\ I_{B}(C3|8000)&= 0.4081; I_{B}(C4|8000)= 0.2875\\ \end{align}\,\! }[/math]
Please note that there is a printing error in the reference book and the importance measure for Computer 4 at 8000 hours is printed as 0.2975 instead of 0.2875.
Results in BlockSim
In BlockSim, the computer system RBD is configured as shown below.
Each computer is modeled using a 1-parameter exponential distribution with the given lambda (failure rate) values.
The reliability equation for the computer system can be viewed via the Equation Viewer. The resulting equation is the same as the one computed in the reference book.
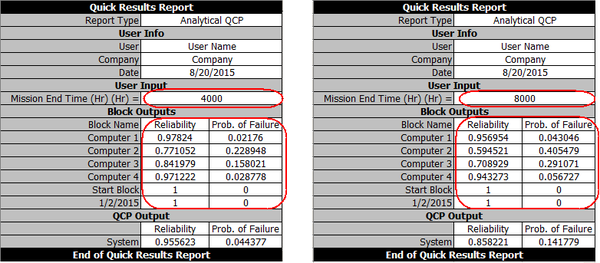
The system reliabilities at 4000 and 8000 hours are calculated in the QCP as R(4000) = 95.56% and R(8000) = 85.82%. The values are the same as the ones in the reference book.
The QCP report (accessed by clicking the Report button in the QCP window) shows the reliabilities of each computer at the given times (4000 and 8000 hours).
The static reliability importance for each computer at 4000 hours is presented below in graphical format, with the values highlighted in red. The color of each bar represents the computer’s reliability.
The static reliability importance for each computer at 8000 hours is shown next.
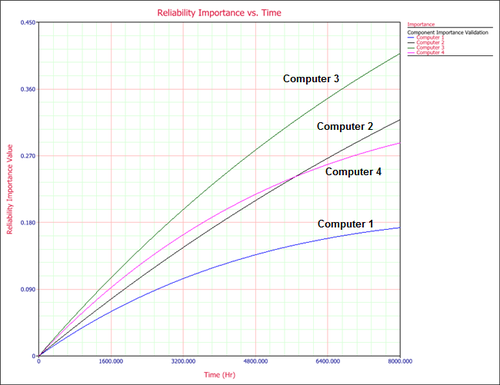
The following plot shows the reliability importance for the individual computers at different times.