Contour Plot Example: Difference between revisions
No edit summary |
Lisa Hacker (talk | contribs) No edit summary |
||
| (14 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
'' | <noinclude>{{Banner Weibull Examples}} | ||
''This example appears in the [https://help.reliasoft.com/reference/life_data_analysis Life data analysis reference].'' | |||
The following data sets represent the times-to-failure for | </noinclude> | ||
'''Using a Contour Plot to Compare Two Designs''' | |||
The design of a product was modified to improve its reliability. The reliability engineers want to determine whether the improvements to the design have significantly improved the product's reliability. The following data sets represent the times-to-failure for the product. At what significance level can the engineers claim that the two designs are different? | |||
<!-- THIS EXAMPLE IS TRANSCLUDED IN PAGE: Life Comparison Examples. IF YOU EDIT THE DATA SET ON THIS PAGE, YOU MUST ALSO EDIT THE DATA SET IN THE PAGE: Life Comparison Wizard. | |||
--> | |||
<center><math>\overset{\text{Old Design}}{\mathop{\begin{array}{*{35}{l}} | <center><math>\overset{\text{Old Design}}{\mathop{\begin{array}{*{35}{l}} | ||
\text{2} & \text{2} & \text{3} & \text{4} & \text{6} & \text{9} \\ | \text{2} & \text{2} & \text{3} & \text{4} & \text{6} & \text{9} \\ | ||
| Line 9: | Line 17: | ||
\text{38} & \text{40} & \text{45} & \text{55} & \text{56} & \text{57} \\ | \text{38} & \text{40} & \text{45} & \text{55} & \text{56} & \text{57} \\ | ||
\text{67} & \text{76} & \text{90} & \text{115} & \text{126} & \text{197} \\ | \text{67} & \text{76} & \text{90} & \text{115} & \text{126} & \text{197} \\ | ||
\end{array}}}\,</math> </center> | \end{array}}}\,\,\!</math> </center> | ||
| Line 15: | Line 23: | ||
\text{15} & \text{32} & \text{61} & \text{67} & \text{75} \\ | \text{15} & \text{32} & \text{61} & \text{67} & \text{75} \\ | ||
\text{116} & \text{148} & \text{178} & \text{181} & \text{183} \\ | \text{116} & \text{148} & \text{178} & \text{181} & \text{183} \\ | ||
\end{array}}}\,</math> </center> | \end{array}}}\,\,\!</math> </center> | ||
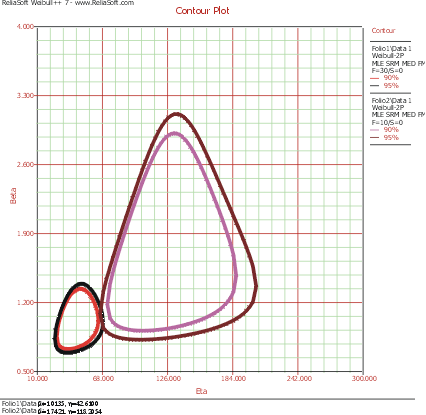
The data sets are entered into separate Weibull++ standard folio data sheets, and then analyzed with the two-parameter Weibull distribution and the maximum likelihood estimation (MLE) method. The following figure shows the contour plots of the data sets superimposed in an overlay plot. This plot is configured to show the contour lines that represent the 90% and 95% confidence levels. | |||
[[Image:lda24_new.png|center|550px| ]] | |||
As you can see, the contours overlap at the 95% confidence level (outer rings), but there is no overlap at the 90% confidence level (inner rings). We can then conclude that there is a statistically significant difference between the data sets at the 90% confidence level. If we wanted to know the exact confidence level (i.e., ''critical confidence level'') at which the two contour plots meet, we would have to incrementally raise the confidence level from 90% until the two contour lines meet. | |||
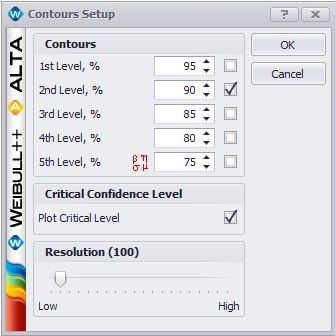
Weibull++ includes a utility for automatically obtaining the critical confidence level. For two contour plots that are superimposed in an overlay plot, the '''Plot Critical Level''' check box will be available in the Contours Setup window, as shown next. | |||
[[Image:Conleveldetector.jpg|center|350px| ]] | |||
The plot critical level is the confidence level at which the contour plots of the two data sets meet at a single point. This is the minimum confidence level at which the contour lines of the two different data sets overlap. At any confidence level below this minimum confidence level, the contour lines of the two data sets will not overlap and there will be a statistically significant difference between the two populations at that level. For the two data sets in this example, the critical confidence level 94.243%. This value will be displayed in the '''Legend''' area of the plot. | |||
Note that due to the calculation resolution and plot precision, the contour lines at the calculated critical level may appear to overlap or have a gap. | |||
Latest revision as of 21:44, 18 September 2023
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.
This example appears in the Life data analysis reference.
Using a Contour Plot to Compare Two Designs
The design of a product was modified to improve its reliability. The reliability engineers want to determine whether the improvements to the design have significantly improved the product's reliability. The following data sets represent the times-to-failure for the product. At what significance level can the engineers claim that the two designs are different?
The data sets are entered into separate Weibull++ standard folio data sheets, and then analyzed with the two-parameter Weibull distribution and the maximum likelihood estimation (MLE) method. The following figure shows the contour plots of the data sets superimposed in an overlay plot. This plot is configured to show the contour lines that represent the 90% and 95% confidence levels.
As you can see, the contours overlap at the 95% confidence level (outer rings), but there is no overlap at the 90% confidence level (inner rings). We can then conclude that there is a statistically significant difference between the data sets at the 90% confidence level. If we wanted to know the exact confidence level (i.e., critical confidence level) at which the two contour plots meet, we would have to incrementally raise the confidence level from 90% until the two contour lines meet.
Weibull++ includes a utility for automatically obtaining the critical confidence level. For two contour plots that are superimposed in an overlay plot, the Plot Critical Level check box will be available in the Contours Setup window, as shown next.
The plot critical level is the confidence level at which the contour plots of the two data sets meet at a single point. This is the minimum confidence level at which the contour lines of the two different data sets overlap. At any confidence level below this minimum confidence level, the contour lines of the two data sets will not overlap and there will be a statistically significant difference between the two populations at that level. For the two data sets in this example, the critical confidence level 94.243%. This value will be displayed in the Legend area of the plot.
Note that due to the calculation resolution and plot precision, the contour lines at the calculated critical level may appear to overlap or have a gap.