Exponential Chi-Squared Example
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.
This example appears in the Life Data Analysis Reference book.
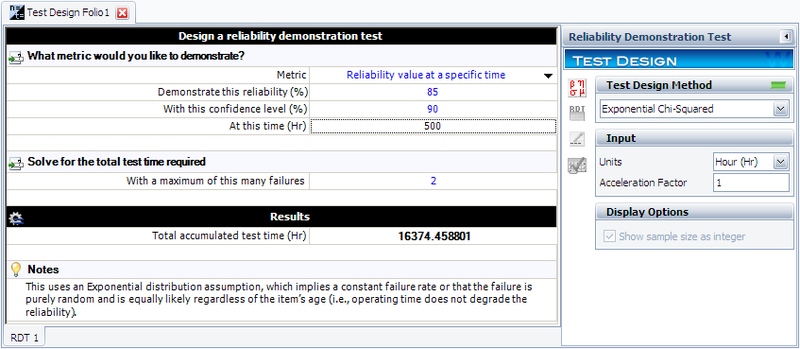
In this example, we will use the exponential chi-squared method to design a test that will demonstrate a reliability of 85% at [math]\displaystyle{ {{t}_{DEMO}}=500\,\! }[/math] hours with a 90% confidence (or [math]\displaystyle{ CL=0.9\,\! }[/math]) if no more than 2 failures occur during the test ([math]\displaystyle{ f=2\,\! }[/math]). The chi-squared value can be determined from tables or the Quick Statistical Reference (QSR) tool in Weibull++. In this example, the value is calculated as:
- [math]\displaystyle{ \chi _{1-CL;2r+2}^{2}=\chi _{0.1;6}^{2}=10.6446\,\! }[/math]
Substituting this into the chi-squared equation, we obtain:
- [math]\displaystyle{ {{T}_{a}}=\frac{\tfrac{500}{-ln(0.85)}\cdot 10.6446}{2}=16,374\text{ hours}\,\! }[/math]
This means that 16,374 hours of total test time needs to be accumulated with no more than two failures in order to demonstrate the specified reliability.
This example solved in Weibull++ is shown next.
Given the test time, one can now solve for the number of units using the chi-squared equation. Similarly, if the number of units is given, one can determine the test time from the chi-squared equation for exponential test design.