Exponential Distribution for Grouped Data Example: Difference between revisions
Chris Kahn (talk | contribs) |
Chris Kahn (talk | contribs) No edit summary |
||
| Line 1: | Line 1: | ||
'''Exponential Distribution for Grouped Data''' | |||
Twenty units were reliability tested with the following results: | |||
{| border="1" align="center" style="border-collapse: collapse;" cellpadding="5" cellspacing="5" | |||
|- | |||
|colspan="2" style="text-align:center"| Table - Life Test Data | |||
|- | |||
|-align="center" | |||
!Number of Units in Group | |||
!Time-to-Failure | |||
|- align="center" | |||
|7 ||100 | |||
|- align="center" | |||
|5 ||200 | |||
|- align="center" | |||
|3 ||300 | |||
|- align="center" | |||
|2 ||400 | |||
|- align="center" | |||
|1 ||500 | |||
|- align="center" | |||
|2 ||600 | |||
|} | |||
8-1. Assuming a two-parameter exponential distribution, estimate the parameters analytically using the MLE method. | |||
8-2. Repeat part 8-1 using Weibull++ (enter the data as grouped data to duplicate the results of 8-1). | |||
8-3. Plot the exponential probability vs. time-to-failure using Weibull++. | |||
8-4. Plot <math>R(t)</math> vs. time using Weibull++. | |||
8-5. Plot the <math>pdf</math> using Weibull++. | |||
8-6. Plot the failure rate vs. time using Weibull++. | |||
8-7. Estimate the parameters analytically using the RRY method (using grouped ranks). | |||
'''Solution''' | |||
8-1. For the two-parameter exponential distribution and for <math>\hat{\gamma }=100</math> hours (first failure), the partial of the log-likelihood function, <math>\Lambda </math>, becomes: | |||
::<math> \begin{align} | |||
\frac{\partial \Lambda }{\partial \lambda }= &\underset{i=1}{\overset{6}{\mathop \sum }}\,{N_i} \left[ \frac{1}{\lambda }-\left( {{T}_{i}}-100 \right) \right]=0\\ | |||
\Rightarrow & 7[\frac{1}{\lambda }-(100-100)]+5[\frac{1}{\lambda}-(200-100)] | |||
+ \ldots +2[\frac{1}{\lambda}-(600-100)]\\ | |||
= & 0\\ | |||
\Rightarrow & \hat{\lambda}=\frac{20}{3100}=0.0065 \text{fr/hr} | |||
\end{align} | |||
</math> | |||
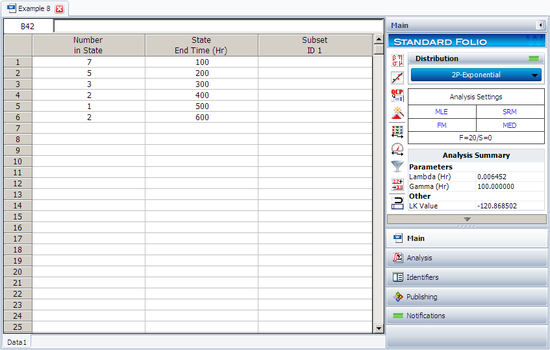
8-2. The data as entered in Weibull++ along with results are shown next. | |||
<br> | |||
<br> | |||
[[Image:Exponential Distribution Example 8 Data.png|center|550px|]] | |||
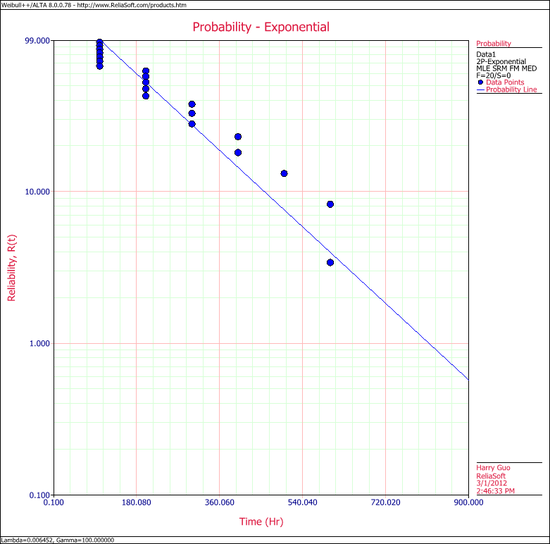
The exponential probability plot is shown next | |||
[[Image:Exponential Distribution Example 8 Plot.png|center|550px|]] | |||
The '''Plot Type''' drop-down box allows you to select different plot types, shown next. | |||
[[Image:Exponential Distribution Example 8 Plot Type.png|center]] | |||
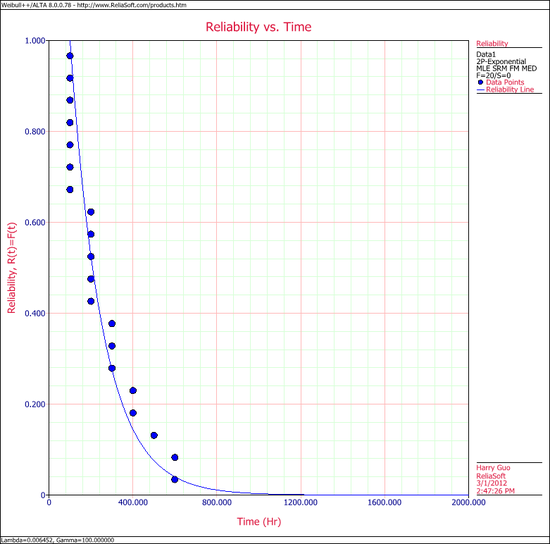
Select '''Reliability vs. Time'''. | |||
[[Image:Exponential Distribution Example 8 Rel Plot.png|center|550px|]] | |||
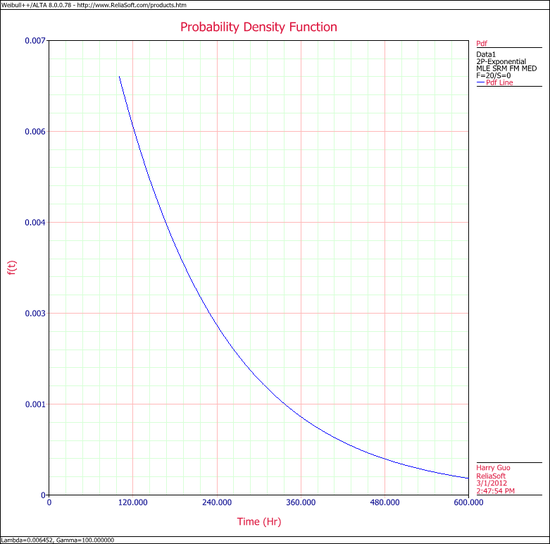
The exponential <math>pdf</math> plot is shown next. | |||
[[Image:Exponential Distribution Example 8 Pdf Plot.png|center|550px|]] | |||
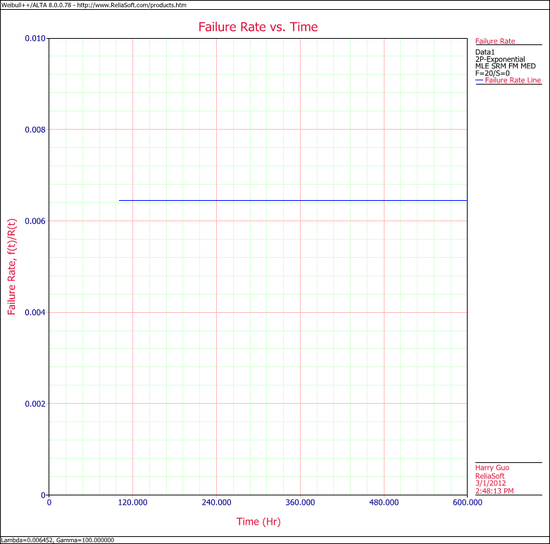
The exponential failure rate plot is shown next. | |||
[[Image:Exponential Distribution Example 8 Failure Rate Plot.png|center|550px|]] | |||
Note that, as described at the beginning of this chapter, the failure rate for the exponential distribution is constant. Also note that the failure rate plot does not exist for times before the location parameter, <math>\gamma </math>, at 100 hours. | |||
8-7. In the case of grouped data, one must be cautious when estimating the parameters using a rank regression method. That is because the median rank values are determined from the total number of failures observed by time <math>{{T}_{i}}</math> where <math>i</math> indicates the group number. In this example the total number of groups is <math>N=6</math> and the total number of units is <math>{{N}_{T}}=20</math>. Thus, the median rank values will be estimated for twenty units and for the total failed units (<math>{{N}_{{{F}_{i}}}}</math>) up to the <math>{{i}^{th}}</math> group, for the <math>{{i}^{th}}</math> rank value. The median ranks values can be found from rank tables or they can be estimated using ReliaSoft's Quick Statistical Reference. | |||
For example, the median rank value of the fourth group will be the <math>{{17}^{th}}</math> rank out of a sample size of twenty units (or 81.945%). | |||
The following table is then constructed (as in Example 2). | |||
<center><math>\begin{matrix} | |||
N & {{N}_{F}} & {{N}_{{{F}_{i}}}} & {{T}_{i}} & F({{T}_{i}}) & {{y}_{i}} & T_{i}^{2} & y_{i}^{2} & {{T}_{i}}{{y}_{i}} \\ | |||
\text{1} & \text{7} & \text{7} & \text{100} & \text{0}\text{.32795} & \text{-0}\text{.3974} & \text{10000} & \text{0}\text{.1579} & \text{-39}\text{.7426} \\ | |||
\text{2} & \text{5} & \text{12} & \text{200} & \text{0}\text{.57374} & \text{-0}\text{.8527} & \text{40000} & \text{0}\text{.7271} & \text{-170}\text{.5402} \\ | |||
\text{3} & \text{3} & \text{15} & \text{300} & \text{0}\text{.72120} & \text{-1}\text{.2772} & \text{90000} & \text{1}\text{.6313} & \text{-383}\text{.1728} \\ | |||
\text{4} & \text{2} & \text{17} & \text{400} & \text{0}\text{.81945} & \text{-1}\text{.7117} & \text{160000} & \text{2}\text{.9301} & \text{-684}\text{.6990} \\ | |||
\text{5} & \text{1} & \text{18} & \text{500} & \text{0}\text{.86853} & \text{-2}\text{.0289} & \text{250000} & \text{4}\text{.1166} & \text{-1014}\text{.4731} \\ | |||
\text{6} & \text{2} & \text{20} & \text{600} & \text{0}\text{.96594} & \text{-3}\text{.3795} & \text{360000} & \text{11}\text{.4211} & \text{-2027}\text{.7085} \\ | |||
\sum_{}^{} & {} & {} & \text{2100} & {} & \text{-9}\text{.6476} & \text{910000} & \text{20}\text{.9842} & \text{-4320}\text{.3362} \\ | |||
\end{matrix}</math></center> | |||
Given the values in the table above, calculate <math>\hat{a}</math> and <math>\hat{b}</math>: | |||
::<math>\begin{align} | |||
& \hat{b}= & \frac{\underset{i=1}{\overset{6}{\mathop{\sum }}}\,{{t}_{i}}{{y}_{i}}-(\underset{i=1}{\overset{6}{\mathop{\sum }}}\,{{t}_{i}})(\underset{i=1}{\overset{6}{\mathop{\sum }}}\,{{y}_{i}})/6}{\underset{i=1}{\overset{6}{\mathop{\sum }}}\,t_{i}^{2}-{{(\underset{i=1}{\overset{6}{\mathop{\sum }}}\,{{t}_{i}})}^{2}}/6} \\ | |||
& & \\ | |||
& \hat{b}= & \frac{-4320.3362-(2100)(-9.6476)/6}{910,000-{{(2100)}^{2}}/6} | |||
\end{align}</math> | |||
or: | |||
::<math>\hat{b}=-0.005392</math> | |||
and: | |||
::<math>\hat{a}=\overline{y}-\hat{b}\overline{t}=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}}}{N}-\hat{b}\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{t}_{i}}}{N}</math> | |||
or: | |||
::<math>\hat{a}=\frac{-9.6476}{6}-(-0.005392)\frac{2100}{6}=0.2793</math> | |||
Therefore: | |||
::<math>\hat{\lambda }=-\hat{b}=-(-0.005392)=0.05392\text{ failures/hour}</math> | |||
and: | |||
::<math>\hat{\gamma }=\frac{\hat{a}}{\hat{\lambda }}=\frac{0.2793}{0.005392}</math> | |||
or: | |||
::<math>\hat{\gamma }\simeq 51.8\text{ hours}</math> | |||
Then: | |||
::<math>f(T)=(0.005392){{e}^{-0.005392(T-51.8)}}</math> | |||
Using Weibull++ , the estimated parameters are: | |||
::<math>\begin{align} | |||
\hat{\lambda }= & 0.0054\text{ failures/hour} \\ | |||
\hat{\gamma }= & 51.82\text{ hours} | |||
\end{align}</math> | |||
The small difference in the values from Weibull++ is due to rounding. In Weibull++ the calculations and the rank values are carried out up to the <math>{{15}^{th}}</math> decimal point. | |||
<br> | |||
Revision as of 00:49, 13 August 2012
Exponential Distribution for Grouped Data
Twenty units were reliability tested with the following results:
| Table - Life Test Data | |
| Number of Units in Group | Time-to-Failure |
|---|---|
| 7 | 100 |
| 5 | 200 |
| 3 | 300 |
| 2 | 400 |
| 1 | 500 |
| 2 | 600 |
8-1. Assuming a two-parameter exponential distribution, estimate the parameters analytically using the MLE method.
8-2. Repeat part 8-1 using Weibull++ (enter the data as grouped data to duplicate the results of 8-1).
8-3. Plot the exponential probability vs. time-to-failure using Weibull++.
8-4. Plot [math]\displaystyle{ R(t) }[/math] vs. time using Weibull++.
8-5. Plot the [math]\displaystyle{ pdf }[/math] using Weibull++.
8-6. Plot the failure rate vs. time using Weibull++.
8-7. Estimate the parameters analytically using the RRY method (using grouped ranks).
Solution
8-1. For the two-parameter exponential distribution and for [math]\displaystyle{ \hat{\gamma }=100 }[/math] hours (first failure), the partial of the log-likelihood function, [math]\displaystyle{ \Lambda }[/math], becomes:
- [math]\displaystyle{ \begin{align} \frac{\partial \Lambda }{\partial \lambda }= &\underset{i=1}{\overset{6}{\mathop \sum }}\,{N_i} \left[ \frac{1}{\lambda }-\left( {{T}_{i}}-100 \right) \right]=0\\ \Rightarrow & 7[\frac{1}{\lambda }-(100-100)]+5[\frac{1}{\lambda}-(200-100)] + \ldots +2[\frac{1}{\lambda}-(600-100)]\\ = & 0\\ \Rightarrow & \hat{\lambda}=\frac{20}{3100}=0.0065 \text{fr/hr} \end{align} }[/math]
8-2. The data as entered in Weibull++ along with results are shown next.
The exponential probability plot is shown next
The Plot Type drop-down box allows you to select different plot types, shown next.
Select Reliability vs. Time.
The exponential [math]\displaystyle{ pdf }[/math] plot is shown next.
The exponential failure rate plot is shown next.
Note that, as described at the beginning of this chapter, the failure rate for the exponential distribution is constant. Also note that the failure rate plot does not exist for times before the location parameter, [math]\displaystyle{ \gamma }[/math], at 100 hours.
8-7. In the case of grouped data, one must be cautious when estimating the parameters using a rank regression method. That is because the median rank values are determined from the total number of failures observed by time [math]\displaystyle{ {{T}_{i}} }[/math] where [math]\displaystyle{ i }[/math] indicates the group number. In this example the total number of groups is [math]\displaystyle{ N=6 }[/math] and the total number of units is [math]\displaystyle{ {{N}_{T}}=20 }[/math]. Thus, the median rank values will be estimated for twenty units and for the total failed units ([math]\displaystyle{ {{N}_{{{F}_{i}}}} }[/math]) up to the [math]\displaystyle{ {{i}^{th}} }[/math] group, for the [math]\displaystyle{ {{i}^{th}} }[/math] rank value. The median ranks values can be found from rank tables or they can be estimated using ReliaSoft's Quick Statistical Reference.
For example, the median rank value of the fourth group will be the [math]\displaystyle{ {{17}^{th}} }[/math] rank out of a sample size of twenty units (or 81.945%).
The following table is then constructed (as in Example 2).
Given the values in the table above, calculate [math]\displaystyle{ \hat{a} }[/math] and [math]\displaystyle{ \hat{b} }[/math]:
- [math]\displaystyle{ \begin{align} & \hat{b}= & \frac{\underset{i=1}{\overset{6}{\mathop{\sum }}}\,{{t}_{i}}{{y}_{i}}-(\underset{i=1}{\overset{6}{\mathop{\sum }}}\,{{t}_{i}})(\underset{i=1}{\overset{6}{\mathop{\sum }}}\,{{y}_{i}})/6}{\underset{i=1}{\overset{6}{\mathop{\sum }}}\,t_{i}^{2}-{{(\underset{i=1}{\overset{6}{\mathop{\sum }}}\,{{t}_{i}})}^{2}}/6} \\ & & \\ & \hat{b}= & \frac{-4320.3362-(2100)(-9.6476)/6}{910,000-{{(2100)}^{2}}/6} \end{align} }[/math]
or:
- [math]\displaystyle{ \hat{b}=-0.005392 }[/math]
and:
- [math]\displaystyle{ \hat{a}=\overline{y}-\hat{b}\overline{t}=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}}}{N}-\hat{b}\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{t}_{i}}}{N} }[/math]
or:
- [math]\displaystyle{ \hat{a}=\frac{-9.6476}{6}-(-0.005392)\frac{2100}{6}=0.2793 }[/math]
Therefore:
- [math]\displaystyle{ \hat{\lambda }=-\hat{b}=-(-0.005392)=0.05392\text{ failures/hour} }[/math]
and:
- [math]\displaystyle{ \hat{\gamma }=\frac{\hat{a}}{\hat{\lambda }}=\frac{0.2793}{0.005392} }[/math]
or:
- [math]\displaystyle{ \hat{\gamma }\simeq 51.8\text{ hours} }[/math]
Then:
- [math]\displaystyle{ f(T)=(0.005392){{e}^{-0.005392(T-51.8)}} }[/math]
Using Weibull++ , the estimated parameters are:
- [math]\displaystyle{ \begin{align} \hat{\lambda }= & 0.0054\text{ failures/hour} \\ \hat{\gamma }= & 51.82\text{ hours} \end{align} }[/math]
The small difference in the values from Weibull++ is due to rounding. In Weibull++ the calculations and the rank values are carried out up to the [math]\displaystyle{ {{15}^{th}} }[/math] decimal point.