Eyring Relationship: Difference between revisions
Chris Kahn (talk | contribs) |
Kate Racaza (talk | contribs) No edit summary |
||
| Line 1: | Line 1: | ||
{{template:ALTABOOK|5}} | {{template:ALTABOOK|5}} | ||
=Introduction= | |||
The Eyring relationship was formulated from quantum mechanics principles [[Reference Appendix D: References|[9]]] and is most often used when thermal stress (temperature) is the acceleration variable. However, the Eyring relationship is also often used for stress variables other than temperature, such as humidity. The relationship is given by: | The Eyring relationship was formulated from quantum mechanics principles [[Reference Appendix D: References|[9]]] and is most often used when thermal stress (temperature) is the acceleration variable. However, the Eyring relationship is also often used for stress variables other than temperature, such as humidity. The relationship is given by: | ||
| Line 49: | Line 47: | ||
<br> | <br> | ||
{{ | ===Acceleration Factor=== | ||
For the Eyring model the acceleration factor is given by: | |||
<br> | |||
::<math>{{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}}=\frac{\tfrac{1}{{{V}_{u}}}\text{ }{{e}^{-\left( A-\tfrac{B}{{{V}_{u}}} \right)}}}{\tfrac{1}{{{V}_{A}}}\text{ }{{e}^{-\left( A-\tfrac{B}{{{V}_{A}}} \right)}}}=\frac{\text{ }{{e}^{\tfrac{B}{{{V}_{u}}}}}}{\text{ }{{e}^{\tfrac{B}{{{V}_{A}}}}}}=\frac{{{V}_{A}}}{{{V}_{u}}}{{e}^{B\left( \tfrac{1}{{{V}_{u}}}-\tfrac{1}{{{V}_{A}}} \right)}}</math> | |||
<br> | |||
=Eyring-Exponential= | |||
The <math>pdf</math> of the 1-parameter exponential distribution is given by: | |||
<br> | |||
::<math>f(t)=\lambda \cdot {{e}^{-\lambda \cdot t}}</math> | |||
<br> | |||
It can be easily shown that the mean life for the 1-parameter exponential distribution (presented in detail [[Distributions Used in Accelerated Testing#The Exponential Distribution|here]]) is given by: | |||
<br> | |||
::<math>\lambda =\frac{1}{m}</math> | |||
<br> | |||
thus: | |||
<br> | |||
::<math>f(t)=\frac{1}{m}\cdot {{e}^{-\tfrac{t}{m}}}</math> | |||
<br> | |||
The Eyring-exponential model <math>pdf</math> can then be obtained by setting <math>m=L(V)</math>: | |||
<br> | |||
::<math>m=L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}</math> | |||
<br> | |||
and substituting for <math>m</math> in the exponential <math>pdf</math> equation: | |||
<br> | |||
::<math>f(t,V)=V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}\cdot t}}</math> | |||
<br> | |||
==Eyring-Exponential Statistical Properties Summary== | |||
====Mean or MTTF==== | |||
The mean, <math>\overline{T},</math> or Mean Time To Failure (MTTF) for the Eyring-exponential is given by: | |||
<br> | |||
::<math>\begin{align} | |||
& \overline{T}= & \int_{0}^{\infty }t\cdot f(t,V)dt=\int_{0}^{\infty }t\cdot V{{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-tV{{e}^{\left( A-\tfrac{B}{V} \right)}}}}dt =\ \frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} | |||
\end{align}</math> | |||
{{ | <br> | ||
====Median==== | |||
The median, <math>\breve{T},</math> | |||
for the Eyring-exponential model is given by: | |||
<br> | |||
::<math>\breve{T}=0.693\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}</math> | |||
<br> | |||
====Mode==== | |||
The mode, <math>\tilde{T},</math> | |||
for the Eyring-exponential model is <math>\tilde{T}=0.</math> | |||
<br> | |||
====Standard Deviation==== | |||
The standard deviation, <math>{{\sigma }_{T}}</math>, for the Eyring-exponential model is given by: | |||
<br> | |||
::<math>{{\sigma }_{T}}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}</math> | |||
<br> | |||
====Eyring-Exponential Reliability Function==== | |||
The Eyring-exponential reliability function is given by: | |||
<br> | |||
::<math>R(T,V)={{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}}</math> | |||
<br> | |||
This function is the complement of the Eyring-exponential cumulative distribution function or: | |||
<br> | |||
::<math>R(T,V)=1-Q(T,V)=1-\int_{0}^{T}f(T,V)dT</math> | |||
<br> | |||
and: | |||
<br> | |||
::<math>R(T,V)=1-\int_{0}^{T}V{{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}}dT={{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}}</math> | |||
<br> | |||
====Conditional Reliability==== | |||
The conditional reliability function for the Eyring-exponential model is given by: | |||
<br> | |||
::<math>R(T,t,V)=\frac{R(T+t,V)}{R(T,V)}=\frac{{{e}^{-\lambda (T+t)}}}{{{e}^{-\lambda T}}}={{e}^{-t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}}</math> | |||
<br> | |||
====Reliable Life==== | |||
For the Eyring-exponential model, the reliable life, or the mission duration for a desired reliability goal, <math>{{t}_{R,}}</math> is given by: | |||
<br> | |||
::<math>R({{t}_{R}},V)={{e}^{-{{t}_{R}}\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}}</math> | |||
<br> | |||
::<math>\ln [R({{t}_{R}},V)]=-{{t}_{R}}\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}</math> | |||
<br> | |||
or: | |||
<br> | |||
::<math>{{t}_{R}}=-\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\ln [R({{t}_{R}},V)]</math> | |||
<br> | |||
==Parameter Estimation== | |||
====Maximum Likelihood Estimation Method==== | |||
The complete exponential log-likelihood function of the Eyring model is composed of two summation portions: | |||
<br> | |||
::<math>\begin{align} | |||
& \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ {{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{e}^{-{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}\cdot {{T}_{i}}}} \right] -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\cdot {{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}\cdot T_{i}^{\prime }+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] | |||
\end{align}</math> | |||
<br> | |||
:where: | |||
<br> | |||
::<math>R_{Li}^{\prime \prime }={{e}^{-T_{Li}^{\prime \prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}}</math> | |||
<br> | |||
::<math>R_{Ri}^{\prime \prime }={{e}^{-T_{Ri}^{\prime \prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}}</math> | |||
<br> | |||
and: | |||
• <math>{{F}_{e}}</math> is the number of groups of exact times-to-failure data points. | |||
<br> | |||
• <math>{{N}_{i}}</math> is the number of times-to-failure in the <math>{{i}^{th}}</math> time-to-failure data group. | |||
<br> | |||
• <math>{{V}_{i}}</math> is the stress level of the <math>{{i}^{th}}</math> group. | |||
<br> | |||
• <math>A</math> is the Eyring parameter (unknown, the first of two parameters to be estimated). | |||
<br> | |||
• <math>B</math> is the second Eyring parameter (unknown, the second of two parameters to be estimated). | |||
<br> | |||
• <math>{{T}_{i}}</math> is the exact failure time of the <math>{{i}^{th}}</math> group. | |||
<br> | |||
• <math>S</math> is the number of groups of suspension data points. | |||
<br> | |||
• <math>N_{i}^{\prime }</math> is the number of suspensions in the <math>{{i}^{th}}</math> group of suspension data points. | |||
<br> | |||
• <math>T_{i}^{\prime }</math> is the running time of the <math>{{i}^{th}}</math> suspension data group. | |||
<br> | |||
• <math>FI</math> is the number of interval data groups. | |||
<br> | |||
• <math>N_{i}^{\prime \prime }</math> is the number of intervals in the <math>{{i}^{th}}</math> group of data intervals. | |||
<br> | |||
• <math>T_{Li}^{\prime \prime }</math> is the beginning of the <math>{{i}^{th}}</math> interval. | |||
<br> | |||
• <math>T_{Ri}^{\prime \prime }</math> is the ending of the <math>{{i}^{th}}</math> interval. | |||
<br> | |||
The solution (parameter estimates) will be found by solving for the parameters <math>\widehat{A}</math> and <math>\widehat{B}</math> so that <math>\tfrac{\partial \Lambda }{\partial A}=0</math> and <math>\tfrac{\partial \Lambda }{\partial B}=0</math> where: | |||
<br> | |||
::<math>\begin{align} | |||
& \frac{\partial \Lambda }{\partial A}= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( 1-{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{T}_{i}} \right)-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}T_{i}^{\prime } \overset{FI}{\mathop{\underset{i=1}{\mathop{-\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\left( T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime } \right){{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} | |||
\end{align}</math> | |||
<br> | |||
::<math>\begin{align} | |||
& \frac{\partial \Lambda }{\partial B}= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left[ {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{T}_{i}}-\frac{1}{{{V}_{i}}} \right]+\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}T_{i}^{\prime } \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\left( T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime } \right){{e}^{A-\tfrac{B}{{{V}_{i}}}}}}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} | |||
\end{align}</math> | |||
<br> | |||
=Eyring-Weibull= | |||
The <math>pdf</math> for 2-parameter Weibull distribution is given by: | |||
<br> | |||
::<math>f(t)=\frac{\beta }{\eta }{{\left( \frac{t}{\eta } \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{t}{\eta } \right)}^{\beta }}}}</math> | |||
<br> | |||
The scale parameter (or characteristic life) of the Weibull distribution is <math>\eta </math> . The Eyring-Weibull model <math>pdf</math> can then be obtained by setting <math>\eta =L(V)</math>: | |||
<br> | |||
::<math>\eta =L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}</math> | |||
<br> | |||
or: | |||
<br> | |||
::<math>\frac{1}{\eta }=V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}</math> | |||
<br> | |||
Substituting for <math>\eta </math> into the Weibull <math>pdf</math> yields: | |||
<br> | |||
::<math>f(t,V)=\beta \cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}{{\left( t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta -1}}{{e}^{-{{\left( t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta }}}}</math> | |||
<br> | |||
{{eyring-weibull stat prop sum}} | |||
===Parameter Estimation=== | |||
<br> | |||
{{eyring-weibull mle}} | |||
{{Example:Eyring}} | {{Example:Eyring}} | ||
Revision as of 11:31, 3 July 2012
Introduction
The Eyring relationship was formulated from quantum mechanics principles [9] and is most often used when thermal stress (temperature) is the acceleration variable. However, the Eyring relationship is also often used for stress variables other than temperature, such as humidity. The relationship is given by:
- [math]\displaystyle{ L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
where:
• [math]\displaystyle{ L }[/math] represents a quantifiable life measure, such as mean life, characteristic life, median life, [math]\displaystyle{ B(x) }[/math] life, etc.
• [math]\displaystyle{ V }[/math] represents the stress level (temperature values are in absolute units: kelvin or degrees Rankine).
• [math]\displaystyle{ A }[/math] is one of the model parameters to be determined.
• [math]\displaystyle{ B }[/math] is another model parameter to be determined.
The Eyring relationship is similar to the Arrhenius relationship. This similarity is more apparent if it is rewritten in the following way:
- [math]\displaystyle{ \begin{align} L(V)=\ & \frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} =\ & \frac{{{e}^{-A}}}{V}{{e}^{\tfrac{B}{V}}} \end{align} }[/math]
or:
- [math]\displaystyle{ L(V)=\frac{1}{V}Const.\cdot {{e}^{\tfrac{B}{V}}} }[/math]
The Arrhenius relationship is given by:
- [math]\displaystyle{ L(V)=C\cdot {{e}^{\tfrac{B}{V}}} }[/math]
Comparing the above equation to the Arrhenius relationship, it can be seen that the only difference between the two relationships is the [math]\displaystyle{ \tfrac{1}{V} }[/math] term above. In general, both relationships yield very similar results. Like the Arrhenius, the Eyring relationship is plotted on a log-reciprocal paper.
Acceleration Factor
For the Eyring model the acceleration factor is given by:
- [math]\displaystyle{ {{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}}=\frac{\tfrac{1}{{{V}_{u}}}\text{ }{{e}^{-\left( A-\tfrac{B}{{{V}_{u}}} \right)}}}{\tfrac{1}{{{V}_{A}}}\text{ }{{e}^{-\left( A-\tfrac{B}{{{V}_{A}}} \right)}}}=\frac{\text{ }{{e}^{\tfrac{B}{{{V}_{u}}}}}}{\text{ }{{e}^{\tfrac{B}{{{V}_{A}}}}}}=\frac{{{V}_{A}}}{{{V}_{u}}}{{e}^{B\left( \tfrac{1}{{{V}_{u}}}-\tfrac{1}{{{V}_{A}}} \right)}} }[/math]
Eyring-Exponential
The [math]\displaystyle{ pdf }[/math] of the 1-parameter exponential distribution is given by:
- [math]\displaystyle{ f(t)=\lambda \cdot {{e}^{-\lambda \cdot t}} }[/math]
It can be easily shown that the mean life for the 1-parameter exponential distribution (presented in detail here) is given by:
- [math]\displaystyle{ \lambda =\frac{1}{m} }[/math]
thus:
- [math]\displaystyle{ f(t)=\frac{1}{m}\cdot {{e}^{-\tfrac{t}{m}}} }[/math]
The Eyring-exponential model [math]\displaystyle{ pdf }[/math] can then be obtained by setting [math]\displaystyle{ m=L(V) }[/math]:
- [math]\displaystyle{ m=L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
and substituting for [math]\displaystyle{ m }[/math] in the exponential [math]\displaystyle{ pdf }[/math] equation:
- [math]\displaystyle{ f(t,V)=V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}\cdot t}} }[/math]
Eyring-Exponential Statistical Properties Summary
Mean or MTTF
The mean, [math]\displaystyle{ \overline{T}, }[/math] or Mean Time To Failure (MTTF) for the Eyring-exponential is given by:
- [math]\displaystyle{ \begin{align} & \overline{T}= & \int_{0}^{\infty }t\cdot f(t,V)dt=\int_{0}^{\infty }t\cdot V{{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-tV{{e}^{\left( A-\tfrac{B}{V} \right)}}}}dt =\ \frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} \end{align} }[/math]
Median
The median, [math]\displaystyle{ \breve{T}, }[/math] for the Eyring-exponential model is given by:
- [math]\displaystyle{ \breve{T}=0.693\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
Mode
The mode, [math]\displaystyle{ \tilde{T}, }[/math] for the Eyring-exponential model is [math]\displaystyle{ \tilde{T}=0. }[/math]
Standard Deviation
The standard deviation, [math]\displaystyle{ {{\sigma }_{T}} }[/math], for the Eyring-exponential model is given by:
- [math]\displaystyle{ {{\sigma }_{T}}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
Eyring-Exponential Reliability Function
The Eyring-exponential reliability function is given by:
- [math]\displaystyle{ R(T,V)={{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
This function is the complement of the Eyring-exponential cumulative distribution function or:
- [math]\displaystyle{ R(T,V)=1-Q(T,V)=1-\int_{0}^{T}f(T,V)dT }[/math]
and:
- [math]\displaystyle{ R(T,V)=1-\int_{0}^{T}V{{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}}dT={{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
Conditional Reliability
The conditional reliability function for the Eyring-exponential model is given by:
- [math]\displaystyle{ R(T,t,V)=\frac{R(T+t,V)}{R(T,V)}=\frac{{{e}^{-\lambda (T+t)}}}{{{e}^{-\lambda T}}}={{e}^{-t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
Reliable Life
For the Eyring-exponential model, the reliable life, or the mission duration for a desired reliability goal, [math]\displaystyle{ {{t}_{R,}} }[/math] is given by:
- [math]\displaystyle{ R({{t}_{R}},V)={{e}^{-{{t}_{R}}\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
- [math]\displaystyle{ \ln [R({{t}_{R}},V)]=-{{t}_{R}}\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} }[/math]
or:
- [math]\displaystyle{ {{t}_{R}}=-\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\ln [R({{t}_{R}},V)] }[/math]
Parameter Estimation
Maximum Likelihood Estimation Method
The complete exponential log-likelihood function of the Eyring model is composed of two summation portions:
- [math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ {{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{e}^{-{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}\cdot {{T}_{i}}}} \right] -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\cdot {{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}\cdot T_{i}^{\prime }+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]
- where:
- [math]\displaystyle{ R_{Li}^{\prime \prime }={{e}^{-T_{Li}^{\prime \prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}} }[/math]
- [math]\displaystyle{ R_{Ri}^{\prime \prime }={{e}^{-T_{Ri}^{\prime \prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}} }[/math]
and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ {{V}_{i}} }[/math] is the stress level of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ A }[/math] is the Eyring parameter (unknown, the first of two parameters to be estimated).
• [math]\displaystyle{ B }[/math] is the second Eyring parameter (unknown, the second of two parameters to be estimated).
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
The solution (parameter estimates) will be found by solving for the parameters [math]\displaystyle{ \widehat{A} }[/math] and [math]\displaystyle{ \widehat{B} }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial A}=0 }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial B}=0 }[/math] where:
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial A}= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( 1-{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{T}_{i}} \right)-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}T_{i}^{\prime } \overset{FI}{\mathop{\underset{i=1}{\mathop{-\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\left( T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime } \right){{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} \end{align} }[/math]
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial B}= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left[ {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{T}_{i}}-\frac{1}{{{V}_{i}}} \right]+\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}T_{i}^{\prime } \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\left( T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime } \right){{e}^{A-\tfrac{B}{{{V}_{i}}}}}}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} \end{align} }[/math]
Eyring-Weibull
The [math]\displaystyle{ pdf }[/math] for 2-parameter Weibull distribution is given by:
- [math]\displaystyle{ f(t)=\frac{\beta }{\eta }{{\left( \frac{t}{\eta } \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{t}{\eta } \right)}^{\beta }}}} }[/math]
The scale parameter (or characteristic life) of the Weibull distribution is [math]\displaystyle{ \eta }[/math] . The Eyring-Weibull model [math]\displaystyle{ pdf }[/math] can then be obtained by setting [math]\displaystyle{ \eta =L(V) }[/math]:
- [math]\displaystyle{ \eta =L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
or:
- [math]\displaystyle{ \frac{1}{\eta }=V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} }[/math]
Substituting for [math]\displaystyle{ \eta }[/math] into the Weibull [math]\displaystyle{ pdf }[/math] yields:
- [math]\displaystyle{ f(t,V)=\beta \cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}{{\left( t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta -1}}{{e}^{-{{\left( t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta }}}} }[/math]
Introduction
The Eyring relationship was formulated from quantum mechanics principles [9] and is most often used when thermal stress (temperature) is the acceleration variable. However, the Eyring relationship is also often used for stress variables other than temperature, such as humidity. The relationship is given by:
- [math]\displaystyle{ L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
where:
• [math]\displaystyle{ L }[/math] represents a quantifiable life measure, such as mean life, characteristic life, median life, [math]\displaystyle{ B(x) }[/math] life, etc.
• [math]\displaystyle{ V }[/math] represents the stress level (temperature values are in absolute units: kelvin or degrees Rankine).
• [math]\displaystyle{ A }[/math] is one of the model parameters to be determined.
• [math]\displaystyle{ B }[/math] is another model parameter to be determined.
The Eyring relationship is similar to the Arrhenius relationship. This similarity is more apparent if it is rewritten in the following way:
- [math]\displaystyle{ \begin{align} L(V)=\ & \frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} =\ & \frac{{{e}^{-A}}}{V}{{e}^{\tfrac{B}{V}}} \end{align} }[/math]
or:
- [math]\displaystyle{ L(V)=\frac{1}{V}Const.\cdot {{e}^{\tfrac{B}{V}}} }[/math]
The Arrhenius relationship is given by:
- [math]\displaystyle{ L(V)=C\cdot {{e}^{\tfrac{B}{V}}} }[/math]
Comparing the above equation to the Arrhenius relationship, it can be seen that the only difference between the two relationships is the [math]\displaystyle{ \tfrac{1}{V} }[/math] term above. In general, both relationships yield very similar results. Like the Arrhenius, the Eyring relationship is plotted on a log-reciprocal paper.
Acceleration Factor
For the Eyring model the acceleration factor is given by:
- [math]\displaystyle{ {{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}}=\frac{\tfrac{1}{{{V}_{u}}}\text{ }{{e}^{-\left( A-\tfrac{B}{{{V}_{u}}} \right)}}}{\tfrac{1}{{{V}_{A}}}\text{ }{{e}^{-\left( A-\tfrac{B}{{{V}_{A}}} \right)}}}=\frac{\text{ }{{e}^{\tfrac{B}{{{V}_{u}}}}}}{\text{ }{{e}^{\tfrac{B}{{{V}_{A}}}}}}=\frac{{{V}_{A}}}{{{V}_{u}}}{{e}^{B\left( \tfrac{1}{{{V}_{u}}}-\tfrac{1}{{{V}_{A}}} \right)}} }[/math]
Eyring-Exponential
The [math]\displaystyle{ pdf }[/math] of the 1-parameter exponential distribution is given by:
- [math]\displaystyle{ f(t)=\lambda \cdot {{e}^{-\lambda \cdot t}} }[/math]
It can be easily shown that the mean life for the 1-parameter exponential distribution (presented in detail here) is given by:
- [math]\displaystyle{ \lambda =\frac{1}{m} }[/math]
thus:
- [math]\displaystyle{ f(t)=\frac{1}{m}\cdot {{e}^{-\tfrac{t}{m}}} }[/math]
The Eyring-exponential model [math]\displaystyle{ pdf }[/math] can then be obtained by setting [math]\displaystyle{ m=L(V) }[/math]:
- [math]\displaystyle{ m=L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
and substituting for [math]\displaystyle{ m }[/math] in the exponential [math]\displaystyle{ pdf }[/math] equation:
- [math]\displaystyle{ f(t,V)=V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}\cdot t}} }[/math]
Eyring-Exponential Statistical Properties Summary
Mean or MTTF
The mean, [math]\displaystyle{ \overline{T}, }[/math] or Mean Time To Failure (MTTF) for the Eyring-exponential is given by:
- [math]\displaystyle{ \begin{align} & \overline{T}= & \int_{0}^{\infty }t\cdot f(t,V)dt=\int_{0}^{\infty }t\cdot V{{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-tV{{e}^{\left( A-\tfrac{B}{V} \right)}}}}dt =\ \frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} \end{align} }[/math]
Median
The median, [math]\displaystyle{ \breve{T}, }[/math] for the Eyring-exponential model is given by:
- [math]\displaystyle{ \breve{T}=0.693\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
Mode
The mode, [math]\displaystyle{ \tilde{T}, }[/math] for the Eyring-exponential model is [math]\displaystyle{ \tilde{T}=0. }[/math]
Standard Deviation
The standard deviation, [math]\displaystyle{ {{\sigma }_{T}} }[/math], for the Eyring-exponential model is given by:
- [math]\displaystyle{ {{\sigma }_{T}}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
Eyring-Exponential Reliability Function
The Eyring-exponential reliability function is given by:
- [math]\displaystyle{ R(T,V)={{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
This function is the complement of the Eyring-exponential cumulative distribution function or:
- [math]\displaystyle{ R(T,V)=1-Q(T,V)=1-\int_{0}^{T}f(T,V)dT }[/math]
and:
- [math]\displaystyle{ R(T,V)=1-\int_{0}^{T}V{{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}}dT={{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
Conditional Reliability
The conditional reliability function for the Eyring-exponential model is given by:
- [math]\displaystyle{ R(T,t,V)=\frac{R(T+t,V)}{R(T,V)}=\frac{{{e}^{-\lambda (T+t)}}}{{{e}^{-\lambda T}}}={{e}^{-t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
Reliable Life
For the Eyring-exponential model, the reliable life, or the mission duration for a desired reliability goal, [math]\displaystyle{ {{t}_{R,}} }[/math] is given by:
- [math]\displaystyle{ R({{t}_{R}},V)={{e}^{-{{t}_{R}}\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
- [math]\displaystyle{ \ln [R({{t}_{R}},V)]=-{{t}_{R}}\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} }[/math]
or:
- [math]\displaystyle{ {{t}_{R}}=-\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\ln [R({{t}_{R}},V)] }[/math]
Parameter Estimation
Maximum Likelihood Estimation Method
The complete exponential log-likelihood function of the Eyring model is composed of two summation portions:
- [math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ {{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{e}^{-{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}\cdot {{T}_{i}}}} \right] -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\cdot {{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}\cdot T_{i}^{\prime }+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]
- where:
- [math]\displaystyle{ R_{Li}^{\prime \prime }={{e}^{-T_{Li}^{\prime \prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}} }[/math]
- [math]\displaystyle{ R_{Ri}^{\prime \prime }={{e}^{-T_{Ri}^{\prime \prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}} }[/math]
and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ {{V}_{i}} }[/math] is the stress level of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ A }[/math] is the Eyring parameter (unknown, the first of two parameters to be estimated).
• [math]\displaystyle{ B }[/math] is the second Eyring parameter (unknown, the second of two parameters to be estimated).
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
The solution (parameter estimates) will be found by solving for the parameters [math]\displaystyle{ \widehat{A} }[/math] and [math]\displaystyle{ \widehat{B} }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial A}=0 }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial B}=0 }[/math] where:
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial A}= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( 1-{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{T}_{i}} \right)-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}T_{i}^{\prime } \overset{FI}{\mathop{\underset{i=1}{\mathop{-\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\left( T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime } \right){{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} \end{align} }[/math]
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial B}= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left[ {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{T}_{i}}-\frac{1}{{{V}_{i}}} \right]+\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}T_{i}^{\prime } \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\left( T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime } \right){{e}^{A-\tfrac{B}{{{V}_{i}}}}}}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} \end{align} }[/math]
Eyring-Weibull
The [math]\displaystyle{ pdf }[/math] for 2-parameter Weibull distribution is given by:
- [math]\displaystyle{ f(t)=\frac{\beta }{\eta }{{\left( \frac{t}{\eta } \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{t}{\eta } \right)}^{\beta }}}} }[/math]
The scale parameter (or characteristic life) of the Weibull distribution is [math]\displaystyle{ \eta }[/math] . The Eyring-Weibull model [math]\displaystyle{ pdf }[/math] can then be obtained by setting [math]\displaystyle{ \eta =L(V) }[/math]:
- [math]\displaystyle{ \eta =L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
or:
- [math]\displaystyle{ \frac{1}{\eta }=V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} }[/math]
Substituting for [math]\displaystyle{ \eta }[/math] into the Weibull [math]\displaystyle{ pdf }[/math] yields:
- [math]\displaystyle{ f(t,V)=\beta \cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}{{\left( t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta -1}}{{e}^{-{{\left( t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta }}}} }[/math]
Template loop detected: Template:Eyring-weibull stat prop sum
Parameter Estimation
Template loop detected: Template:Eyring-weibull mle
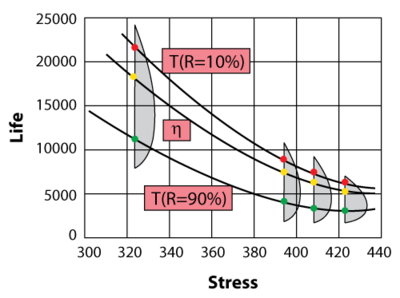
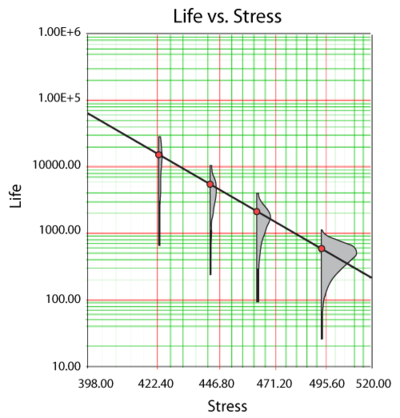
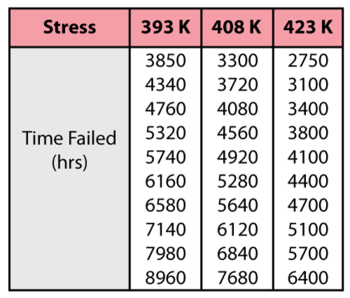
Consider the following times-to-failure data at three different stress levels.
The data set was entered into the ALTA standard folio and analyzed using the Eyring-Weibull model, yielding:
- [math]\displaystyle{ \widehat{\beta }=4.29186497\,\! }[/math]
- [math]\displaystyle{ \widehat{A}=-11.08784624\,\! }[/math]
- [math]\displaystyle{ \widehat{B}=1454.08635742\,\! }[/math]
Once the parameters of the model are defined, other life measures can be directly obtained using the appropriate equations. For example, the MTTF can be obtained for the use stress level of 323 K by using:
- [math]\displaystyle{ \overline{T}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\cdot \Gamma \left( \frac{1}{\beta }+1 \right)\,\! }[/math]
or:
- [math]\displaystyle{ \begin{align} & \overline{T}= & \frac{1}{323}{{e}^{-\left( -11.08784624-\tfrac{1454.08635742}{323} \right)}}\cdot \Gamma \left( \frac{1}{4.29186497}+1 \right) =16,610\text{ }hr \end{align}\,\! }[/math]
Template loop detected: Template:Erying-log
Template loop detected: Template:Generalized eyring
Template loop detected: Template:Eyring confidence bounds
Parameter Estimation
Introduction
The Eyring relationship was formulated from quantum mechanics principles [9] and is most often used when thermal stress (temperature) is the acceleration variable. However, the Eyring relationship is also often used for stress variables other than temperature, such as humidity. The relationship is given by:
- [math]\displaystyle{ L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
where:
• [math]\displaystyle{ L }[/math] represents a quantifiable life measure, such as mean life, characteristic life, median life, [math]\displaystyle{ B(x) }[/math] life, etc.
• [math]\displaystyle{ V }[/math] represents the stress level (temperature values are in absolute units: kelvin or degrees Rankine).
• [math]\displaystyle{ A }[/math] is one of the model parameters to be determined.
• [math]\displaystyle{ B }[/math] is another model parameter to be determined.
The Eyring relationship is similar to the Arrhenius relationship. This similarity is more apparent if it is rewritten in the following way:
- [math]\displaystyle{ \begin{align} L(V)=\ & \frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} =\ & \frac{{{e}^{-A}}}{V}{{e}^{\tfrac{B}{V}}} \end{align} }[/math]
or:
- [math]\displaystyle{ L(V)=\frac{1}{V}Const.\cdot {{e}^{\tfrac{B}{V}}} }[/math]
The Arrhenius relationship is given by:
- [math]\displaystyle{ L(V)=C\cdot {{e}^{\tfrac{B}{V}}} }[/math]
Comparing the above equation to the Arrhenius relationship, it can be seen that the only difference between the two relationships is the [math]\displaystyle{ \tfrac{1}{V} }[/math] term above. In general, both relationships yield very similar results. Like the Arrhenius, the Eyring relationship is plotted on a log-reciprocal paper.
Acceleration Factor
For the Eyring model the acceleration factor is given by:
- [math]\displaystyle{ {{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}}=\frac{\tfrac{1}{{{V}_{u}}}\text{ }{{e}^{-\left( A-\tfrac{B}{{{V}_{u}}} \right)}}}{\tfrac{1}{{{V}_{A}}}\text{ }{{e}^{-\left( A-\tfrac{B}{{{V}_{A}}} \right)}}}=\frac{\text{ }{{e}^{\tfrac{B}{{{V}_{u}}}}}}{\text{ }{{e}^{\tfrac{B}{{{V}_{A}}}}}}=\frac{{{V}_{A}}}{{{V}_{u}}}{{e}^{B\left( \tfrac{1}{{{V}_{u}}}-\tfrac{1}{{{V}_{A}}} \right)}} }[/math]
Eyring-Exponential
The [math]\displaystyle{ pdf }[/math] of the 1-parameter exponential distribution is given by:
- [math]\displaystyle{ f(t)=\lambda \cdot {{e}^{-\lambda \cdot t}} }[/math]
It can be easily shown that the mean life for the 1-parameter exponential distribution (presented in detail here) is given by:
- [math]\displaystyle{ \lambda =\frac{1}{m} }[/math]
thus:
- [math]\displaystyle{ f(t)=\frac{1}{m}\cdot {{e}^{-\tfrac{t}{m}}} }[/math]
The Eyring-exponential model [math]\displaystyle{ pdf }[/math] can then be obtained by setting [math]\displaystyle{ m=L(V) }[/math]:
- [math]\displaystyle{ m=L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
and substituting for [math]\displaystyle{ m }[/math] in the exponential [math]\displaystyle{ pdf }[/math] equation:
- [math]\displaystyle{ f(t,V)=V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}\cdot t}} }[/math]
Eyring-Exponential Statistical Properties Summary
Mean or MTTF
The mean, [math]\displaystyle{ \overline{T}, }[/math] or Mean Time To Failure (MTTF) for the Eyring-exponential is given by:
- [math]\displaystyle{ \begin{align} & \overline{T}= & \int_{0}^{\infty }t\cdot f(t,V)dt=\int_{0}^{\infty }t\cdot V{{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-tV{{e}^{\left( A-\tfrac{B}{V} \right)}}}}dt =\ \frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} \end{align} }[/math]
Median
The median, [math]\displaystyle{ \breve{T}, }[/math] for the Eyring-exponential model is given by:
- [math]\displaystyle{ \breve{T}=0.693\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
Mode
The mode, [math]\displaystyle{ \tilde{T}, }[/math] for the Eyring-exponential model is [math]\displaystyle{ \tilde{T}=0. }[/math]
Standard Deviation
The standard deviation, [math]\displaystyle{ {{\sigma }_{T}} }[/math], for the Eyring-exponential model is given by:
- [math]\displaystyle{ {{\sigma }_{T}}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
Eyring-Exponential Reliability Function
The Eyring-exponential reliability function is given by:
- [math]\displaystyle{ R(T,V)={{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
This function is the complement of the Eyring-exponential cumulative distribution function or:
- [math]\displaystyle{ R(T,V)=1-Q(T,V)=1-\int_{0}^{T}f(T,V)dT }[/math]
and:
- [math]\displaystyle{ R(T,V)=1-\int_{0}^{T}V{{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}}dT={{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
Conditional Reliability
The conditional reliability function for the Eyring-exponential model is given by:
- [math]\displaystyle{ R(T,t,V)=\frac{R(T+t,V)}{R(T,V)}=\frac{{{e}^{-\lambda (T+t)}}}{{{e}^{-\lambda T}}}={{e}^{-t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
Reliable Life
For the Eyring-exponential model, the reliable life, or the mission duration for a desired reliability goal, [math]\displaystyle{ {{t}_{R,}} }[/math] is given by:
- [math]\displaystyle{ R({{t}_{R}},V)={{e}^{-{{t}_{R}}\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
- [math]\displaystyle{ \ln [R({{t}_{R}},V)]=-{{t}_{R}}\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} }[/math]
or:
- [math]\displaystyle{ {{t}_{R}}=-\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\ln [R({{t}_{R}},V)] }[/math]
Parameter Estimation
Maximum Likelihood Estimation Method
The complete exponential log-likelihood function of the Eyring model is composed of two summation portions:
- [math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ {{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{e}^{-{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}\cdot {{T}_{i}}}} \right] -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\cdot {{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}\cdot T_{i}^{\prime }+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]
- where:
- [math]\displaystyle{ R_{Li}^{\prime \prime }={{e}^{-T_{Li}^{\prime \prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}} }[/math]
- [math]\displaystyle{ R_{Ri}^{\prime \prime }={{e}^{-T_{Ri}^{\prime \prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}} }[/math]
and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ {{V}_{i}} }[/math] is the stress level of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ A }[/math] is the Eyring parameter (unknown, the first of two parameters to be estimated).
• [math]\displaystyle{ B }[/math] is the second Eyring parameter (unknown, the second of two parameters to be estimated).
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
The solution (parameter estimates) will be found by solving for the parameters [math]\displaystyle{ \widehat{A} }[/math] and [math]\displaystyle{ \widehat{B} }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial A}=0 }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial B}=0 }[/math] where:
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial A}= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( 1-{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{T}_{i}} \right)-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}T_{i}^{\prime } \overset{FI}{\mathop{\underset{i=1}{\mathop{-\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\left( T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime } \right){{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} \end{align} }[/math]
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial B}= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left[ {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{T}_{i}}-\frac{1}{{{V}_{i}}} \right]+\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}T_{i}^{\prime } \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\left( T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime } \right){{e}^{A-\tfrac{B}{{{V}_{i}}}}}}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} \end{align} }[/math]
Eyring-Weibull
The [math]\displaystyle{ pdf }[/math] for 2-parameter Weibull distribution is given by:
- [math]\displaystyle{ f(t)=\frac{\beta }{\eta }{{\left( \frac{t}{\eta } \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{t}{\eta } \right)}^{\beta }}}} }[/math]
The scale parameter (or characteristic life) of the Weibull distribution is [math]\displaystyle{ \eta }[/math] . The Eyring-Weibull model [math]\displaystyle{ pdf }[/math] can then be obtained by setting [math]\displaystyle{ \eta =L(V) }[/math]:
- [math]\displaystyle{ \eta =L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
or:
- [math]\displaystyle{ \frac{1}{\eta }=V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} }[/math]
Substituting for [math]\displaystyle{ \eta }[/math] into the Weibull [math]\displaystyle{ pdf }[/math] yields:
- [math]\displaystyle{ f(t,V)=\beta \cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}{{\left( t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta -1}}{{e}^{-{{\left( t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta }}}} }[/math]
Template loop detected: Template:Eyring-weibull stat prop sum
Parameter Estimation
Template loop detected: Template:Eyring-weibull mle
Consider the following times-to-failure data at three different stress levels.
The data set was entered into the ALTA standard folio and analyzed using the Eyring-Weibull model, yielding:
- [math]\displaystyle{ \widehat{\beta }=4.29186497\,\! }[/math]
- [math]\displaystyle{ \widehat{A}=-11.08784624\,\! }[/math]
- [math]\displaystyle{ \widehat{B}=1454.08635742\,\! }[/math]
Once the parameters of the model are defined, other life measures can be directly obtained using the appropriate equations. For example, the MTTF can be obtained for the use stress level of 323 K by using:
- [math]\displaystyle{ \overline{T}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\cdot \Gamma \left( \frac{1}{\beta }+1 \right)\,\! }[/math]
or:
- [math]\displaystyle{ \begin{align} & \overline{T}= & \frac{1}{323}{{e}^{-\left( -11.08784624-\tfrac{1454.08635742}{323} \right)}}\cdot \Gamma \left( \frac{1}{4.29186497}+1 \right) =16,610\text{ }hr \end{align}\,\! }[/math]
Template loop detected: Template:Erying-log
Template loop detected: Template:Generalized eyring
Template loop detected: Template:Eyring confidence bounds
Consider the following times-to-failure data at three different stress levels.
The data set was entered into the ALTA standard folio and analyzed using the Eyring-Weibull model, yielding:
- [math]\displaystyle{ \widehat{\beta }=4.29186497\,\! }[/math]
- [math]\displaystyle{ \widehat{A}=-11.08784624\,\! }[/math]
- [math]\displaystyle{ \widehat{B}=1454.08635742\,\! }[/math]
Once the parameters of the model are defined, other life measures can be directly obtained using the appropriate equations. For example, the MTTF can be obtained for the use stress level of 323 K by using:
- [math]\displaystyle{ \overline{T}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\cdot \Gamma \left( \frac{1}{\beta }+1 \right)\,\! }[/math]
or:
- [math]\displaystyle{ \begin{align} & \overline{T}= & \frac{1}{323}{{e}^{-\left( -11.08784624-\tfrac{1454.08635742}{323} \right)}}\cdot \Gamma \left( \frac{1}{4.29186497}+1 \right) =16,610\text{ }hr \end{align}\,\! }[/math]
Introduction
The Eyring relationship was formulated from quantum mechanics principles [9] and is most often used when thermal stress (temperature) is the acceleration variable. However, the Eyring relationship is also often used for stress variables other than temperature, such as humidity. The relationship is given by:
- [math]\displaystyle{ L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
where:
• [math]\displaystyle{ L }[/math] represents a quantifiable life measure, such as mean life, characteristic life, median life, [math]\displaystyle{ B(x) }[/math] life, etc.
• [math]\displaystyle{ V }[/math] represents the stress level (temperature values are in absolute units: kelvin or degrees Rankine).
• [math]\displaystyle{ A }[/math] is one of the model parameters to be determined.
• [math]\displaystyle{ B }[/math] is another model parameter to be determined.
The Eyring relationship is similar to the Arrhenius relationship. This similarity is more apparent if it is rewritten in the following way:
- [math]\displaystyle{ \begin{align} L(V)=\ & \frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} =\ & \frac{{{e}^{-A}}}{V}{{e}^{\tfrac{B}{V}}} \end{align} }[/math]
or:
- [math]\displaystyle{ L(V)=\frac{1}{V}Const.\cdot {{e}^{\tfrac{B}{V}}} }[/math]
The Arrhenius relationship is given by:
- [math]\displaystyle{ L(V)=C\cdot {{e}^{\tfrac{B}{V}}} }[/math]
Comparing the above equation to the Arrhenius relationship, it can be seen that the only difference between the two relationships is the [math]\displaystyle{ \tfrac{1}{V} }[/math] term above. In general, both relationships yield very similar results. Like the Arrhenius, the Eyring relationship is plotted on a log-reciprocal paper.
Acceleration Factor
For the Eyring model the acceleration factor is given by:
- [math]\displaystyle{ {{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}}=\frac{\tfrac{1}{{{V}_{u}}}\text{ }{{e}^{-\left( A-\tfrac{B}{{{V}_{u}}} \right)}}}{\tfrac{1}{{{V}_{A}}}\text{ }{{e}^{-\left( A-\tfrac{B}{{{V}_{A}}} \right)}}}=\frac{\text{ }{{e}^{\tfrac{B}{{{V}_{u}}}}}}{\text{ }{{e}^{\tfrac{B}{{{V}_{A}}}}}}=\frac{{{V}_{A}}}{{{V}_{u}}}{{e}^{B\left( \tfrac{1}{{{V}_{u}}}-\tfrac{1}{{{V}_{A}}} \right)}} }[/math]
Eyring-Exponential
The [math]\displaystyle{ pdf }[/math] of the 1-parameter exponential distribution is given by:
- [math]\displaystyle{ f(t)=\lambda \cdot {{e}^{-\lambda \cdot t}} }[/math]
It can be easily shown that the mean life for the 1-parameter exponential distribution (presented in detail here) is given by:
- [math]\displaystyle{ \lambda =\frac{1}{m} }[/math]
thus:
- [math]\displaystyle{ f(t)=\frac{1}{m}\cdot {{e}^{-\tfrac{t}{m}}} }[/math]
The Eyring-exponential model [math]\displaystyle{ pdf }[/math] can then be obtained by setting [math]\displaystyle{ m=L(V) }[/math]:
- [math]\displaystyle{ m=L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
and substituting for [math]\displaystyle{ m }[/math] in the exponential [math]\displaystyle{ pdf }[/math] equation:
- [math]\displaystyle{ f(t,V)=V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}\cdot t}} }[/math]
Eyring-Exponential Statistical Properties Summary
Mean or MTTF
The mean, [math]\displaystyle{ \overline{T}, }[/math] or Mean Time To Failure (MTTF) for the Eyring-exponential is given by:
- [math]\displaystyle{ \begin{align} & \overline{T}= & \int_{0}^{\infty }t\cdot f(t,V)dt=\int_{0}^{\infty }t\cdot V{{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-tV{{e}^{\left( A-\tfrac{B}{V} \right)}}}}dt =\ \frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} \end{align} }[/math]
Median
The median, [math]\displaystyle{ \breve{T}, }[/math] for the Eyring-exponential model is given by:
- [math]\displaystyle{ \breve{T}=0.693\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
Mode
The mode, [math]\displaystyle{ \tilde{T}, }[/math] for the Eyring-exponential model is [math]\displaystyle{ \tilde{T}=0. }[/math]
Standard Deviation
The standard deviation, [math]\displaystyle{ {{\sigma }_{T}} }[/math], for the Eyring-exponential model is given by:
- [math]\displaystyle{ {{\sigma }_{T}}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
Eyring-Exponential Reliability Function
The Eyring-exponential reliability function is given by:
- [math]\displaystyle{ R(T,V)={{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
This function is the complement of the Eyring-exponential cumulative distribution function or:
- [math]\displaystyle{ R(T,V)=1-Q(T,V)=1-\int_{0}^{T}f(T,V)dT }[/math]
and:
- [math]\displaystyle{ R(T,V)=1-\int_{0}^{T}V{{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}}dT={{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
Conditional Reliability
The conditional reliability function for the Eyring-exponential model is given by:
- [math]\displaystyle{ R(T,t,V)=\frac{R(T+t,V)}{R(T,V)}=\frac{{{e}^{-\lambda (T+t)}}}{{{e}^{-\lambda T}}}={{e}^{-t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
Reliable Life
For the Eyring-exponential model, the reliable life, or the mission duration for a desired reliability goal, [math]\displaystyle{ {{t}_{R,}} }[/math] is given by:
- [math]\displaystyle{ R({{t}_{R}},V)={{e}^{-{{t}_{R}}\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
- [math]\displaystyle{ \ln [R({{t}_{R}},V)]=-{{t}_{R}}\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} }[/math]
or:
- [math]\displaystyle{ {{t}_{R}}=-\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\ln [R({{t}_{R}},V)] }[/math]
Parameter Estimation
Maximum Likelihood Estimation Method
The complete exponential log-likelihood function of the Eyring model is composed of two summation portions:
- [math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ {{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{e}^{-{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}\cdot {{T}_{i}}}} \right] -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\cdot {{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}\cdot T_{i}^{\prime }+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]
- where:
- [math]\displaystyle{ R_{Li}^{\prime \prime }={{e}^{-T_{Li}^{\prime \prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}} }[/math]
- [math]\displaystyle{ R_{Ri}^{\prime \prime }={{e}^{-T_{Ri}^{\prime \prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}} }[/math]
and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ {{V}_{i}} }[/math] is the stress level of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ A }[/math] is the Eyring parameter (unknown, the first of two parameters to be estimated).
• [math]\displaystyle{ B }[/math] is the second Eyring parameter (unknown, the second of two parameters to be estimated).
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
The solution (parameter estimates) will be found by solving for the parameters [math]\displaystyle{ \widehat{A} }[/math] and [math]\displaystyle{ \widehat{B} }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial A}=0 }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial B}=0 }[/math] where:
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial A}= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( 1-{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{T}_{i}} \right)-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}T_{i}^{\prime } \overset{FI}{\mathop{\underset{i=1}{\mathop{-\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\left( T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime } \right){{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} \end{align} }[/math]
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial B}= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left[ {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{T}_{i}}-\frac{1}{{{V}_{i}}} \right]+\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}T_{i}^{\prime } \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\left( T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime } \right){{e}^{A-\tfrac{B}{{{V}_{i}}}}}}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} \end{align} }[/math]
Eyring-Weibull
The [math]\displaystyle{ pdf }[/math] for 2-parameter Weibull distribution is given by:
- [math]\displaystyle{ f(t)=\frac{\beta }{\eta }{{\left( \frac{t}{\eta } \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{t}{\eta } \right)}^{\beta }}}} }[/math]
The scale parameter (or characteristic life) of the Weibull distribution is [math]\displaystyle{ \eta }[/math] . The Eyring-Weibull model [math]\displaystyle{ pdf }[/math] can then be obtained by setting [math]\displaystyle{ \eta =L(V) }[/math]:
- [math]\displaystyle{ \eta =L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
or:
- [math]\displaystyle{ \frac{1}{\eta }=V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} }[/math]
Substituting for [math]\displaystyle{ \eta }[/math] into the Weibull [math]\displaystyle{ pdf }[/math] yields:
- [math]\displaystyle{ f(t,V)=\beta \cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}{{\left( t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta -1}}{{e}^{-{{\left( t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta }}}} }[/math]
Template loop detected: Template:Eyring-weibull stat prop sum
Parameter Estimation
Template loop detected: Template:Eyring-weibull mle
Consider the following times-to-failure data at three different stress levels.
The data set was entered into the ALTA standard folio and analyzed using the Eyring-Weibull model, yielding:
- [math]\displaystyle{ \widehat{\beta }=4.29186497\,\! }[/math]
- [math]\displaystyle{ \widehat{A}=-11.08784624\,\! }[/math]
- [math]\displaystyle{ \widehat{B}=1454.08635742\,\! }[/math]
Once the parameters of the model are defined, other life measures can be directly obtained using the appropriate equations. For example, the MTTF can be obtained for the use stress level of 323 K by using:
- [math]\displaystyle{ \overline{T}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\cdot \Gamma \left( \frac{1}{\beta }+1 \right)\,\! }[/math]
or:
- [math]\displaystyle{ \begin{align} & \overline{T}= & \frac{1}{323}{{e}^{-\left( -11.08784624-\tfrac{1454.08635742}{323} \right)}}\cdot \Gamma \left( \frac{1}{4.29186497}+1 \right) =16,610\text{ }hr \end{align}\,\! }[/math]
Template loop detected: Template:Erying-log
Template loop detected: Template:Generalized eyring
Template loop detected: Template:Eyring confidence bounds
Introduction
The Eyring relationship was formulated from quantum mechanics principles [9] and is most often used when thermal stress (temperature) is the acceleration variable. However, the Eyring relationship is also often used for stress variables other than temperature, such as humidity. The relationship is given by:
- [math]\displaystyle{ L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
where:
• [math]\displaystyle{ L }[/math] represents a quantifiable life measure, such as mean life, characteristic life, median life, [math]\displaystyle{ B(x) }[/math] life, etc.
• [math]\displaystyle{ V }[/math] represents the stress level (temperature values are in absolute units: kelvin or degrees Rankine).
• [math]\displaystyle{ A }[/math] is one of the model parameters to be determined.
• [math]\displaystyle{ B }[/math] is another model parameter to be determined.
The Eyring relationship is similar to the Arrhenius relationship. This similarity is more apparent if it is rewritten in the following way:
- [math]\displaystyle{ \begin{align} L(V)=\ & \frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} =\ & \frac{{{e}^{-A}}}{V}{{e}^{\tfrac{B}{V}}} \end{align} }[/math]
or:
- [math]\displaystyle{ L(V)=\frac{1}{V}Const.\cdot {{e}^{\tfrac{B}{V}}} }[/math]
The Arrhenius relationship is given by:
- [math]\displaystyle{ L(V)=C\cdot {{e}^{\tfrac{B}{V}}} }[/math]
Comparing the above equation to the Arrhenius relationship, it can be seen that the only difference between the two relationships is the [math]\displaystyle{ \tfrac{1}{V} }[/math] term above. In general, both relationships yield very similar results. Like the Arrhenius, the Eyring relationship is plotted on a log-reciprocal paper.
Acceleration Factor
For the Eyring model the acceleration factor is given by:
- [math]\displaystyle{ {{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}}=\frac{\tfrac{1}{{{V}_{u}}}\text{ }{{e}^{-\left( A-\tfrac{B}{{{V}_{u}}} \right)}}}{\tfrac{1}{{{V}_{A}}}\text{ }{{e}^{-\left( A-\tfrac{B}{{{V}_{A}}} \right)}}}=\frac{\text{ }{{e}^{\tfrac{B}{{{V}_{u}}}}}}{\text{ }{{e}^{\tfrac{B}{{{V}_{A}}}}}}=\frac{{{V}_{A}}}{{{V}_{u}}}{{e}^{B\left( \tfrac{1}{{{V}_{u}}}-\tfrac{1}{{{V}_{A}}} \right)}} }[/math]
Eyring-Exponential
The [math]\displaystyle{ pdf }[/math] of the 1-parameter exponential distribution is given by:
- [math]\displaystyle{ f(t)=\lambda \cdot {{e}^{-\lambda \cdot t}} }[/math]
It can be easily shown that the mean life for the 1-parameter exponential distribution (presented in detail here) is given by:
- [math]\displaystyle{ \lambda =\frac{1}{m} }[/math]
thus:
- [math]\displaystyle{ f(t)=\frac{1}{m}\cdot {{e}^{-\tfrac{t}{m}}} }[/math]
The Eyring-exponential model [math]\displaystyle{ pdf }[/math] can then be obtained by setting [math]\displaystyle{ m=L(V) }[/math]:
- [math]\displaystyle{ m=L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
and substituting for [math]\displaystyle{ m }[/math] in the exponential [math]\displaystyle{ pdf }[/math] equation:
- [math]\displaystyle{ f(t,V)=V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}\cdot t}} }[/math]
Eyring-Exponential Statistical Properties Summary
Mean or MTTF
The mean, [math]\displaystyle{ \overline{T}, }[/math] or Mean Time To Failure (MTTF) for the Eyring-exponential is given by:
- [math]\displaystyle{ \begin{align} & \overline{T}= & \int_{0}^{\infty }t\cdot f(t,V)dt=\int_{0}^{\infty }t\cdot V{{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-tV{{e}^{\left( A-\tfrac{B}{V} \right)}}}}dt =\ \frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} \end{align} }[/math]
Median
The median, [math]\displaystyle{ \breve{T}, }[/math] for the Eyring-exponential model is given by:
- [math]\displaystyle{ \breve{T}=0.693\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
Mode
The mode, [math]\displaystyle{ \tilde{T}, }[/math] for the Eyring-exponential model is [math]\displaystyle{ \tilde{T}=0. }[/math]
Standard Deviation
The standard deviation, [math]\displaystyle{ {{\sigma }_{T}} }[/math], for the Eyring-exponential model is given by:
- [math]\displaystyle{ {{\sigma }_{T}}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
Eyring-Exponential Reliability Function
The Eyring-exponential reliability function is given by:
- [math]\displaystyle{ R(T,V)={{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
This function is the complement of the Eyring-exponential cumulative distribution function or:
- [math]\displaystyle{ R(T,V)=1-Q(T,V)=1-\int_{0}^{T}f(T,V)dT }[/math]
and:
- [math]\displaystyle{ R(T,V)=1-\int_{0}^{T}V{{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}}dT={{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
Conditional Reliability
The conditional reliability function for the Eyring-exponential model is given by:
- [math]\displaystyle{ R(T,t,V)=\frac{R(T+t,V)}{R(T,V)}=\frac{{{e}^{-\lambda (T+t)}}}{{{e}^{-\lambda T}}}={{e}^{-t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
Reliable Life
For the Eyring-exponential model, the reliable life, or the mission duration for a desired reliability goal, [math]\displaystyle{ {{t}_{R,}} }[/math] is given by:
- [math]\displaystyle{ R({{t}_{R}},V)={{e}^{-{{t}_{R}}\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
- [math]\displaystyle{ \ln [R({{t}_{R}},V)]=-{{t}_{R}}\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} }[/math]
or:
- [math]\displaystyle{ {{t}_{R}}=-\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\ln [R({{t}_{R}},V)] }[/math]
Parameter Estimation
Maximum Likelihood Estimation Method
The complete exponential log-likelihood function of the Eyring model is composed of two summation portions:
- [math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ {{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{e}^{-{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}\cdot {{T}_{i}}}} \right] -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\cdot {{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}\cdot T_{i}^{\prime }+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]
- where:
- [math]\displaystyle{ R_{Li}^{\prime \prime }={{e}^{-T_{Li}^{\prime \prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}} }[/math]
- [math]\displaystyle{ R_{Ri}^{\prime \prime }={{e}^{-T_{Ri}^{\prime \prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}} }[/math]
and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ {{V}_{i}} }[/math] is the stress level of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ A }[/math] is the Eyring parameter (unknown, the first of two parameters to be estimated).
• [math]\displaystyle{ B }[/math] is the second Eyring parameter (unknown, the second of two parameters to be estimated).
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
The solution (parameter estimates) will be found by solving for the parameters [math]\displaystyle{ \widehat{A} }[/math] and [math]\displaystyle{ \widehat{B} }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial A}=0 }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial B}=0 }[/math] where:
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial A}= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( 1-{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{T}_{i}} \right)-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}T_{i}^{\prime } \overset{FI}{\mathop{\underset{i=1}{\mathop{-\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\left( T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime } \right){{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} \end{align} }[/math]
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial B}= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left[ {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{T}_{i}}-\frac{1}{{{V}_{i}}} \right]+\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}T_{i}^{\prime } \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\left( T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime } \right){{e}^{A-\tfrac{B}{{{V}_{i}}}}}}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} \end{align} }[/math]
Eyring-Weibull
The [math]\displaystyle{ pdf }[/math] for 2-parameter Weibull distribution is given by:
- [math]\displaystyle{ f(t)=\frac{\beta }{\eta }{{\left( \frac{t}{\eta } \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{t}{\eta } \right)}^{\beta }}}} }[/math]
The scale parameter (or characteristic life) of the Weibull distribution is [math]\displaystyle{ \eta }[/math] . The Eyring-Weibull model [math]\displaystyle{ pdf }[/math] can then be obtained by setting [math]\displaystyle{ \eta =L(V) }[/math]:
- [math]\displaystyle{ \eta =L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
or:
- [math]\displaystyle{ \frac{1}{\eta }=V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} }[/math]
Substituting for [math]\displaystyle{ \eta }[/math] into the Weibull [math]\displaystyle{ pdf }[/math] yields:
- [math]\displaystyle{ f(t,V)=\beta \cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}{{\left( t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta -1}}{{e}^{-{{\left( t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta }}}} }[/math]
Template loop detected: Template:Eyring-weibull stat prop sum
Parameter Estimation
Template loop detected: Template:Eyring-weibull mle
Consider the following times-to-failure data at three different stress levels.
The data set was entered into the ALTA standard folio and analyzed using the Eyring-Weibull model, yielding:
- [math]\displaystyle{ \widehat{\beta }=4.29186497\,\! }[/math]
- [math]\displaystyle{ \widehat{A}=-11.08784624\,\! }[/math]
- [math]\displaystyle{ \widehat{B}=1454.08635742\,\! }[/math]
Once the parameters of the model are defined, other life measures can be directly obtained using the appropriate equations. For example, the MTTF can be obtained for the use stress level of 323 K by using:
- [math]\displaystyle{ \overline{T}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\cdot \Gamma \left( \frac{1}{\beta }+1 \right)\,\! }[/math]
or:
- [math]\displaystyle{ \begin{align} & \overline{T}= & \frac{1}{323}{{e}^{-\left( -11.08784624-\tfrac{1454.08635742}{323} \right)}}\cdot \Gamma \left( \frac{1}{4.29186497}+1 \right) =16,610\text{ }hr \end{align}\,\! }[/math]
Template loop detected: Template:Erying-log
Template loop detected: Template:Generalized eyring
Template loop detected: Template:Eyring confidence bounds
Introduction
The Eyring relationship was formulated from quantum mechanics principles [9] and is most often used when thermal stress (temperature) is the acceleration variable. However, the Eyring relationship is also often used for stress variables other than temperature, such as humidity. The relationship is given by:
- [math]\displaystyle{ L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
where:
• [math]\displaystyle{ L }[/math] represents a quantifiable life measure, such as mean life, characteristic life, median life, [math]\displaystyle{ B(x) }[/math] life, etc.
• [math]\displaystyle{ V }[/math] represents the stress level (temperature values are in absolute units: kelvin or degrees Rankine).
• [math]\displaystyle{ A }[/math] is one of the model parameters to be determined.
• [math]\displaystyle{ B }[/math] is another model parameter to be determined.
The Eyring relationship is similar to the Arrhenius relationship. This similarity is more apparent if it is rewritten in the following way:
- [math]\displaystyle{ \begin{align} L(V)=\ & \frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} =\ & \frac{{{e}^{-A}}}{V}{{e}^{\tfrac{B}{V}}} \end{align} }[/math]
or:
- [math]\displaystyle{ L(V)=\frac{1}{V}Const.\cdot {{e}^{\tfrac{B}{V}}} }[/math]
The Arrhenius relationship is given by:
- [math]\displaystyle{ L(V)=C\cdot {{e}^{\tfrac{B}{V}}} }[/math]
Comparing the above equation to the Arrhenius relationship, it can be seen that the only difference between the two relationships is the [math]\displaystyle{ \tfrac{1}{V} }[/math] term above. In general, both relationships yield very similar results. Like the Arrhenius, the Eyring relationship is plotted on a log-reciprocal paper.
Acceleration Factor
For the Eyring model the acceleration factor is given by:
- [math]\displaystyle{ {{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}}=\frac{\tfrac{1}{{{V}_{u}}}\text{ }{{e}^{-\left( A-\tfrac{B}{{{V}_{u}}} \right)}}}{\tfrac{1}{{{V}_{A}}}\text{ }{{e}^{-\left( A-\tfrac{B}{{{V}_{A}}} \right)}}}=\frac{\text{ }{{e}^{\tfrac{B}{{{V}_{u}}}}}}{\text{ }{{e}^{\tfrac{B}{{{V}_{A}}}}}}=\frac{{{V}_{A}}}{{{V}_{u}}}{{e}^{B\left( \tfrac{1}{{{V}_{u}}}-\tfrac{1}{{{V}_{A}}} \right)}} }[/math]
Eyring-Exponential
The [math]\displaystyle{ pdf }[/math] of the 1-parameter exponential distribution is given by:
- [math]\displaystyle{ f(t)=\lambda \cdot {{e}^{-\lambda \cdot t}} }[/math]
It can be easily shown that the mean life for the 1-parameter exponential distribution (presented in detail here) is given by:
- [math]\displaystyle{ \lambda =\frac{1}{m} }[/math]
thus:
- [math]\displaystyle{ f(t)=\frac{1}{m}\cdot {{e}^{-\tfrac{t}{m}}} }[/math]
The Eyring-exponential model [math]\displaystyle{ pdf }[/math] can then be obtained by setting [math]\displaystyle{ m=L(V) }[/math]:
- [math]\displaystyle{ m=L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
and substituting for [math]\displaystyle{ m }[/math] in the exponential [math]\displaystyle{ pdf }[/math] equation:
- [math]\displaystyle{ f(t,V)=V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}\cdot t}} }[/math]
Eyring-Exponential Statistical Properties Summary
Mean or MTTF
The mean, [math]\displaystyle{ \overline{T}, }[/math] or Mean Time To Failure (MTTF) for the Eyring-exponential is given by:
- [math]\displaystyle{ \begin{align} & \overline{T}= & \int_{0}^{\infty }t\cdot f(t,V)dt=\int_{0}^{\infty }t\cdot V{{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-tV{{e}^{\left( A-\tfrac{B}{V} \right)}}}}dt =\ \frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} \end{align} }[/math]
Median
The median, [math]\displaystyle{ \breve{T}, }[/math] for the Eyring-exponential model is given by:
- [math]\displaystyle{ \breve{T}=0.693\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
Mode
The mode, [math]\displaystyle{ \tilde{T}, }[/math] for the Eyring-exponential model is [math]\displaystyle{ \tilde{T}=0. }[/math]
Standard Deviation
The standard deviation, [math]\displaystyle{ {{\sigma }_{T}} }[/math], for the Eyring-exponential model is given by:
- [math]\displaystyle{ {{\sigma }_{T}}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
Eyring-Exponential Reliability Function
The Eyring-exponential reliability function is given by:
- [math]\displaystyle{ R(T,V)={{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
This function is the complement of the Eyring-exponential cumulative distribution function or:
- [math]\displaystyle{ R(T,V)=1-Q(T,V)=1-\int_{0}^{T}f(T,V)dT }[/math]
and:
- [math]\displaystyle{ R(T,V)=1-\int_{0}^{T}V{{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}}dT={{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
Conditional Reliability
The conditional reliability function for the Eyring-exponential model is given by:
- [math]\displaystyle{ R(T,t,V)=\frac{R(T+t,V)}{R(T,V)}=\frac{{{e}^{-\lambda (T+t)}}}{{{e}^{-\lambda T}}}={{e}^{-t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
Reliable Life
For the Eyring-exponential model, the reliable life, or the mission duration for a desired reliability goal, [math]\displaystyle{ {{t}_{R,}} }[/math] is given by:
- [math]\displaystyle{ R({{t}_{R}},V)={{e}^{-{{t}_{R}}\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
- [math]\displaystyle{ \ln [R({{t}_{R}},V)]=-{{t}_{R}}\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} }[/math]
or:
- [math]\displaystyle{ {{t}_{R}}=-\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\ln [R({{t}_{R}},V)] }[/math]
Parameter Estimation
Maximum Likelihood Estimation Method
The complete exponential log-likelihood function of the Eyring model is composed of two summation portions:
- [math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ {{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{e}^{-{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}\cdot {{T}_{i}}}} \right] -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\cdot {{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}\cdot T_{i}^{\prime }+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]
- where:
- [math]\displaystyle{ R_{Li}^{\prime \prime }={{e}^{-T_{Li}^{\prime \prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}} }[/math]
- [math]\displaystyle{ R_{Ri}^{\prime \prime }={{e}^{-T_{Ri}^{\prime \prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}} }[/math]
and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ {{V}_{i}} }[/math] is the stress level of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ A }[/math] is the Eyring parameter (unknown, the first of two parameters to be estimated).
• [math]\displaystyle{ B }[/math] is the second Eyring parameter (unknown, the second of two parameters to be estimated).
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
The solution (parameter estimates) will be found by solving for the parameters [math]\displaystyle{ \widehat{A} }[/math] and [math]\displaystyle{ \widehat{B} }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial A}=0 }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial B}=0 }[/math] where:
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial A}= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( 1-{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{T}_{i}} \right)-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}T_{i}^{\prime } \overset{FI}{\mathop{\underset{i=1}{\mathop{-\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\left( T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime } \right){{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} \end{align} }[/math]
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial B}= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left[ {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{T}_{i}}-\frac{1}{{{V}_{i}}} \right]+\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}T_{i}^{\prime } \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\left( T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime } \right){{e}^{A-\tfrac{B}{{{V}_{i}}}}}}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} \end{align} }[/math]
Eyring-Weibull
The [math]\displaystyle{ pdf }[/math] for 2-parameter Weibull distribution is given by:
- [math]\displaystyle{ f(t)=\frac{\beta }{\eta }{{\left( \frac{t}{\eta } \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{t}{\eta } \right)}^{\beta }}}} }[/math]
The scale parameter (or characteristic life) of the Weibull distribution is [math]\displaystyle{ \eta }[/math] . The Eyring-Weibull model [math]\displaystyle{ pdf }[/math] can then be obtained by setting [math]\displaystyle{ \eta =L(V) }[/math]:
- [math]\displaystyle{ \eta =L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
or:
- [math]\displaystyle{ \frac{1}{\eta }=V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} }[/math]
Substituting for [math]\displaystyle{ \eta }[/math] into the Weibull [math]\displaystyle{ pdf }[/math] yields:
- [math]\displaystyle{ f(t,V)=\beta \cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}{{\left( t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta -1}}{{e}^{-{{\left( t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta }}}} }[/math]
Template loop detected: Template:Eyring-weibull stat prop sum
Parameter Estimation
Template loop detected: Template:Eyring-weibull mle
Consider the following times-to-failure data at three different stress levels.
The data set was entered into the ALTA standard folio and analyzed using the Eyring-Weibull model, yielding:
- [math]\displaystyle{ \widehat{\beta }=4.29186497\,\! }[/math]
- [math]\displaystyle{ \widehat{A}=-11.08784624\,\! }[/math]
- [math]\displaystyle{ \widehat{B}=1454.08635742\,\! }[/math]
Once the parameters of the model are defined, other life measures can be directly obtained using the appropriate equations. For example, the MTTF can be obtained for the use stress level of 323 K by using:
- [math]\displaystyle{ \overline{T}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\cdot \Gamma \left( \frac{1}{\beta }+1 \right)\,\! }[/math]
or:
- [math]\displaystyle{ \begin{align} & \overline{T}= & \frac{1}{323}{{e}^{-\left( -11.08784624-\tfrac{1454.08635742}{323} \right)}}\cdot \Gamma \left( \frac{1}{4.29186497}+1 \right) =16,610\text{ }hr \end{align}\,\! }[/math]
Template loop detected: Template:Erying-log
Template loop detected: Template:Generalized eyring
Template loop detected: Template:Eyring confidence bounds