Fleet Data Analysis
Fleet analysis is similar to the repairable systems analysis described in the previous chapter. The main difference is that a fleet of systems is considered and the models are applied to the fleet failures rather than to the system failures. In other words, repairable system analysis models the number of system failures versus system time; whereas fleet analysis models the number of fleet failures versus fleet time.
The main motivation for fleet analysis is to enable the application of the Crow Extended model for fielded data. In many cases, reliability improvements might be necessary on systems that are already in the field. These types of reliability improvements are essentially delayed fixes (BD modes) as described in Chapter 9.
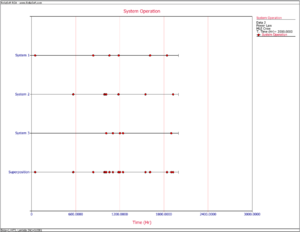
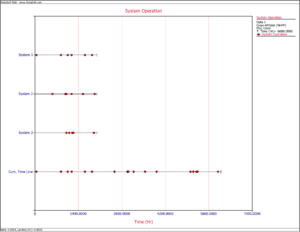
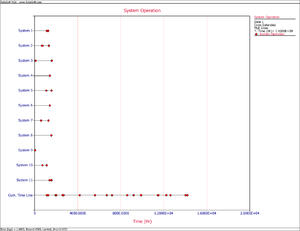
Recall from the Crow Extended chapter that in order to make projections using the Crow Extended model, the [math]\displaystyle{ \beta }[/math] of the combined A and BD modes should be equal to 1. Since the failure intensity in a fielded system might be changing over time (e.g. increasing if the system wears out), this assumption might be violated. In such a scenario, the Crow Extended model cannot be used. However, if a fleet of systems is considered and the number of fleet failures versus fleet time is modeled, the failures might become random. This is because there is a mixture of systems within a fleet, new and old, and when the failures of this mixture of systems are viewed from a cumulative fleet time point of view, they may be random. Figures Repairable and Fleet illustrate this concept. Figure Repairable shows the number of failures over system age. It can be clearly seen that as the systems age, the intensity of the failures increases (wearout). The superposition system line, which brings the failures from the different systems under a single timeline, also illustrates this observation. On the other hand, if you take the same four systems and combine their failures from a fleet perspective, and consider fleet failures over cumulative fleet hours, then the failures seem to be random. Figure Fleet illustrates this concept in the System Operation plot when you consider the Cum. Time Line. In this case, the [math]\displaystyle{ \beta }[/math] of the fleet will be equal to 1 and the Crow Extended model can be used for quantifying the effects of future reliability improvements on the fleet.
Methodology
Figures Repairable and Fleet illustrate that the difference between repairable system data analysis and fleet analysis is the way that the dataset is treated. In fleet analysis, the time-to-failure data from each system is stacked to a cumulative timeline. For example, consider the two systems in Table 13.2.
| Table 13.2 - System data | ||
| System | Failure Times (hr) | End Time (hr) |
|---|---|---|
| 1 | 3, 7 | 10 |
| 2 | 4, 9, 13 | 15 |
The data set is first converted to an accumulated timeline, as follows:
- • System 1 is considered first. The accumulated timeline is therefore 3 and 7 hours.
- • System 1's End Time is 10 hours. System 2's first failure is at 4 hours. This failure time is added to System 1's End Time to give an accumulated failure time of 14 hours.
- • The second failure for System 2 occurred 5 hours after the first failure. This time interval is added to the accumulated timeline to give 19 hours.
- • The third failure for System 2 occurred 4 hours after the second failure. The accumulated failure time is 19 + 4 = 23 hours.
- • System 2's end time is 15 hours, or 2 hours after the last failure. The total accumulated operating time for the fleet is 25 hours (23 + 2 = 25).
In general, the accumulated operating time [math]\displaystyle{ {{Y}_{j}} }[/math] is calculated by:
- [math]\displaystyle{ {{Y}_{j}}={{X}_{i,q}}+\underset{q=1}{\overset{K-1}{\mathop \sum }}\,{{T}_{q}},\text{ }m=1,2,...,N }[/math]
- where:
- • [math]\displaystyle{ {{X}_{i,q}} }[/math] is the [math]\displaystyle{ {{i}^{th}} }[/math] failure of the [math]\displaystyle{ {{q}^{th}} }[/math] system
- • [math]\displaystyle{ {{T}_{q}} }[/math] is the end time of the [math]\displaystyle{ {{q}^{th}} }[/math] system
- • [math]\displaystyle{ K }[/math] is the total number of systems
- • [math]\displaystyle{ N }[/math] is the total number of failures from all systems ( [math]\displaystyle{ N=\underset{j=1}{\overset{K}{\mathop{\sum }}}\,{{N}_{q}} }[/math] )
As this example demonstrates, the accumulated timeline is determined based on the order of the systems. So if you consider the data in Table 13.2 by taking System 2 first, the accumulated timeline would be: 4, 9, 13, 18, 22, with an end time of 25. Therefore, the order in which the systems are considered is somewhat important. However, in the next step of the analysis the data from the accumulated timeline will be grouped into time intervals, effectively eliminating the importance of the order of the systems. Keep in mind that this will NOT always be true. This is true only when the order of the systems was random to begin with. If there is some logic/pattern in the order of the systems, then it will remain even if the cumulative timeline is converted to grouped data. For example, consider a system that wears out with age. This means that more failures will be observed as this system ages and these failures will occur more frequently. Within a fleet of such systems, there will be new and old systems in operation. If the dataset collected is considered from the newest to the oldest system, then even if the data points are grouped, the pattern of fewer failures at the beginning and more failures at later time intervals will still be present. If the objective of the analysis is to determine the difference between newer and older systems, then that order for the data will be acceptable. However, if the objective of the analysis is to determine the reliability of the fleet, then the systems should be randomly ordered.
Fleet Data Analysis
Once the accumulated timeline has been generated, it is then converted into grouped data. To accomplish this, a group interval is required. The group interval length should be chosen so that it is representative of the data. Also note that the intervals do not have to be of equal length. Once the data points have been grouped, the parameters can be obtained using maximum likelihood estimation as described in the Grouped Data Analysis section of the Crow-AMSAA (NHPP) chapter. The data from the table above can be grouped into 5 hour intervals. This interval length is sufficiently large to insure that there are failures within each interval. The grouped data set is given in the following table.
| Grouped data | |
| Failures in Interval | Interval End Time |
|---|---|
| 1 | 5 |
| 1 | 10 |
| 1 | 15 |
| 1 | 20 |
| 1 | 25 |
The Crow-AMSAA model for Grouped Failure Times is used for the data in Table 13.3 and the parameters of the model are solved by satisfying the following maximum likelihood equations (Chapter 5).
- [math]\displaystyle{ \begin{matrix} \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} \\ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i-1}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 \\ \end{matrix} }[/math]
Fleet Analysis Example
The following table presents data for a fleet of 27 systems. A cycle is a complete history from overhaul to overhaul. The failure history for the last completed cycle for each system is recorded. This is a random sample of data from the fleet. These systems are in the order in which they were selected. Suppose the intervals to group the current data are 10000, 20000, 30000, 40000 and the final interval is defined by the termination time. Conduct the fleet analysis.
| Sample fleet data | |||
| System | Cycle Time [math]\displaystyle{ {{T}_{j}} }[/math] | Number of failures [math]\displaystyle{ {{N}_{j}} }[/math] | Failure Time [math]\displaystyle{ {{X}_{ij}} }[/math] |
|---|---|---|---|
| 1 | 1396 | 1 | 1396 |
| 2 | 4497 | 1 | 4497 |
| 3 | 525 | 1 | 525 |
| 4 | 1232 | 1 | 1232 |
| 5 | 227 | 1 | 227 |
| 6 | 135 | 1 | 135 |
| 7 | 19 | 1 | 19 |
| 8 | 812 | 1 | 812 |
| 9 | 2024 | 1 | 2024 |
| 10 | 943 | 2 | 316, 943 |
| 11 | 60 | 1 | 60 |
| 12 | 4234 | 2 | 4233, 4234 |
| 13 | 2527 | 2 | 1877, 2527 |
| 14 | 2105 | 2 | 2074, 2105 |
| 15 | 5079 | 1 | 5079 |
| 16 | 577 | 2 | 546, 577 |
| 17 | 4085 | 2 | 453, 4085 |
| 18 | 1023 | 1 | 1023 |
| 19 | 161 | 1 | 161 |
| 20 | 4767 | 2 | 36, 4767 |
| 21 | 6228 | 3 | 3795, 4375, 6228 |
| 22 | 68 | 1 | 68 |
| 23 | 1830 | 1 | 1830 |
| 24 | 1241 | 1 | 1241 |
| 25 | 2573 | 2 | 871, 2573 |
| 26 | 3556 | 1 | 3556 |
| 27 | 186 | 1 | 186 |
| Total | 52110 | 37 | |
Solution
The sample fleet data set can be grouped into 10000, 20000, 30000, 4000 and 52110 time intervals. The following table gives the grouped data.
| Grouped data | |
| Time | Observed Failures |
|---|---|
| 10000 | 8 |
| 20000 | 16 |
| 30000 | 22 |
| 40000 | 27 |
| 52110 | 37 |
Based on the above time intervals, the maximum likelihood estimates of [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] for this data set are then given by:
- [math]\displaystyle{ \begin{matrix} \widehat{\lambda }=0.00147 \\ \widehat{\beta }=0.93328 \\ \end{matrix} }[/math]
The next figure shows the System Operation plot.
Fleet analysis is similar to the repairable systems analysis described in the previous chapter. The main difference is that a fleet of systems is considered and the models are applied to the fleet failures rather than to the system failures. In other words, repairable system analysis models the number of system failures versus system time; whereas fleet analysis models the number of fleet failures versus fleet time.
The main motivation for fleet analysis is to enable the application of the Crow Extended model for fielded data. In many cases, reliability improvements might be necessary on systems that are already in the field. These types of reliability improvements are essentially delayed fixes (BD modes) as described in Chapter 9.
Recall from the Crow Extended chapter that in order to make projections using the Crow Extended model, the [math]\displaystyle{ \beta }[/math] of the combined A and BD modes should be equal to 1. Since the failure intensity in a fielded system might be changing over time (e.g. increasing if the system wears out), this assumption might be violated. In such a scenario, the Crow Extended model cannot be used. However, if a fleet of systems is considered and the number of fleet failures versus fleet time is modeled, the failures might become random. This is because there is a mixture of systems within a fleet, new and old, and when the failures of this mixture of systems are viewed from a cumulative fleet time point of view, they may be random. Figures Repairable and Fleet illustrate this concept. Figure Repairable shows the number of failures over system age. It can be clearly seen that as the systems age, the intensity of the failures increases (wearout). The superposition system line, which brings the failures from the different systems under a single timeline, also illustrates this observation. On the other hand, if you take the same four systems and combine their failures from a fleet perspective, and consider fleet failures over cumulative fleet hours, then the failures seem to be random. Figure Fleet illustrates this concept in the System Operation plot when you consider the Cum. Time Line. In this case, the [math]\displaystyle{ \beta }[/math] of the fleet will be equal to 1 and the Crow Extended model can be used for quantifying the effects of future reliability improvements on the fleet.
Methodology
Figures Repairable and Fleet illustrate that the difference between repairable system data analysis and fleet analysis is the way that the dataset is treated. In fleet analysis, the time-to-failure data from each system is stacked to a cumulative timeline. For example, consider the two systems in Table 13.2.
| Table 13.2 - System data | ||
| System | Failure Times (hr) | End Time (hr) |
|---|---|---|
| 1 | 3, 7 | 10 |
| 2 | 4, 9, 13 | 15 |
The data set is first converted to an accumulated timeline, as follows:
- • System 1 is considered first. The accumulated timeline is therefore 3 and 7 hours.
- • System 1's End Time is 10 hours. System 2's first failure is at 4 hours. This failure time is added to System 1's End Time to give an accumulated failure time of 14 hours.
- • The second failure for System 2 occurred 5 hours after the first failure. This time interval is added to the accumulated timeline to give 19 hours.
- • The third failure for System 2 occurred 4 hours after the second failure. The accumulated failure time is 19 + 4 = 23 hours.
- • System 2's end time is 15 hours, or 2 hours after the last failure. The total accumulated operating time for the fleet is 25 hours (23 + 2 = 25).
In general, the accumulated operating time [math]\displaystyle{ {{Y}_{j}} }[/math] is calculated by:
- [math]\displaystyle{ {{Y}_{j}}={{X}_{i,q}}+\underset{q=1}{\overset{K-1}{\mathop \sum }}\,{{T}_{q}},\text{ }m=1,2,...,N }[/math]
- where:
- • [math]\displaystyle{ {{X}_{i,q}} }[/math] is the [math]\displaystyle{ {{i}^{th}} }[/math] failure of the [math]\displaystyle{ {{q}^{th}} }[/math] system
- • [math]\displaystyle{ {{T}_{q}} }[/math] is the end time of the [math]\displaystyle{ {{q}^{th}} }[/math] system
- • [math]\displaystyle{ K }[/math] is the total number of systems
- • [math]\displaystyle{ N }[/math] is the total number of failures from all systems ( [math]\displaystyle{ N=\underset{j=1}{\overset{K}{\mathop{\sum }}}\,{{N}_{q}} }[/math] )
As this example demonstrates, the accumulated timeline is determined based on the order of the systems. So if you consider the data in Table 13.2 by taking System 2 first, the accumulated timeline would be: 4, 9, 13, 18, 22, with an end time of 25. Therefore, the order in which the systems are considered is somewhat important. However, in the next step of the analysis the data from the accumulated timeline will be grouped into time intervals, effectively eliminating the importance of the order of the systems. Keep in mind that this will NOT always be true. This is true only when the order of the systems was random to begin with. If there is some logic/pattern in the order of the systems, then it will remain even if the cumulative timeline is converted to grouped data. For example, consider a system that wears out with age. This means that more failures will be observed as this system ages and these failures will occur more frequently. Within a fleet of such systems, there will be new and old systems in operation. If the dataset collected is considered from the newest to the oldest system, then even if the data points are grouped, the pattern of fewer failures at the beginning and more failures at later time intervals will still be present. If the objective of the analysis is to determine the difference between newer and older systems, then that order for the data will be acceptable. However, if the objective of the analysis is to determine the reliability of the fleet, then the systems should be randomly ordered.
Fleet Data Analysis
Once the accumulated timeline has been generated, it is then converted into grouped data. To accomplish this, a group interval is required. The group interval length should be chosen so that it is representative of the data. Also note that the intervals do not have to be of equal length. Once the data points have been grouped, the parameters can be obtained using maximum likelihood estimation as described in the Grouped Data Analysis section of the Crow-AMSAA (NHPP) chapter. The data from the table above can be grouped into 5 hour intervals. This interval length is sufficiently large to insure that there are failures within each interval. The grouped data set is given in the following table.
| Grouped data | |
| Failures in Interval | Interval End Time |
|---|---|
| 1 | 5 |
| 1 | 10 |
| 1 | 15 |
| 1 | 20 |
| 1 | 25 |
The Crow-AMSAA model for Grouped Failure Times is used for the data in Table 13.3 and the parameters of the model are solved by satisfying the following maximum likelihood equations (Chapter 5).
- [math]\displaystyle{ \begin{matrix} \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} \\ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i-1}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 \\ \end{matrix} }[/math]
Fleet Analysis Example
The following table presents data for a fleet of 27 systems. A cycle is a complete history from overhaul to overhaul. The failure history for the last completed cycle for each system is recorded. This is a random sample of data from the fleet. These systems are in the order in which they were selected. Suppose the intervals to group the current data are 10000, 20000, 30000, 40000 and the final interval is defined by the termination time. Conduct the fleet analysis.
| Sample fleet data | |||
| System | Cycle Time [math]\displaystyle{ {{T}_{j}} }[/math] | Number of failures [math]\displaystyle{ {{N}_{j}} }[/math] | Failure Time [math]\displaystyle{ {{X}_{ij}} }[/math] |
|---|---|---|---|
| 1 | 1396 | 1 | 1396 |
| 2 | 4497 | 1 | 4497 |
| 3 | 525 | 1 | 525 |
| 4 | 1232 | 1 | 1232 |
| 5 | 227 | 1 | 227 |
| 6 | 135 | 1 | 135 |
| 7 | 19 | 1 | 19 |
| 8 | 812 | 1 | 812 |
| 9 | 2024 | 1 | 2024 |
| 10 | 943 | 2 | 316, 943 |
| 11 | 60 | 1 | 60 |
| 12 | 4234 | 2 | 4233, 4234 |
| 13 | 2527 | 2 | 1877, 2527 |
| 14 | 2105 | 2 | 2074, 2105 |
| 15 | 5079 | 1 | 5079 |
| 16 | 577 | 2 | 546, 577 |
| 17 | 4085 | 2 | 453, 4085 |
| 18 | 1023 | 1 | 1023 |
| 19 | 161 | 1 | 161 |
| 20 | 4767 | 2 | 36, 4767 |
| 21 | 6228 | 3 | 3795, 4375, 6228 |
| 22 | 68 | 1 | 68 |
| 23 | 1830 | 1 | 1830 |
| 24 | 1241 | 1 | 1241 |
| 25 | 2573 | 2 | 871, 2573 |
| 26 | 3556 | 1 | 3556 |
| 27 | 186 | 1 | 186 |
| Total | 52110 | 37 | |
Solution
The sample fleet data set can be grouped into 10000, 20000, 30000, 4000 and 52110 time intervals. The following table gives the grouped data.
| Grouped data | |
| Time | Observed Failures |
|---|---|
| 10000 | 8 |
| 20000 | 16 |
| 30000 | 22 |
| 40000 | 27 |
| 52110 | 37 |
Based on the above time intervals, the maximum likelihood estimates of [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] for this data set are then given by:
- [math]\displaystyle{ \begin{matrix} \widehat{\lambda }=0.00147 \\ \widehat{\beta }=0.93328 \\ \end{matrix} }[/math]
The next figure shows the System Operation plot.
Template loop detected: Template:Applying the crow extended model to fleet data
Template loop detected: Template:Confidence bounds fleet rsa
General Examples
Predicting the Number of Failures for Fleet Operation
Eleven systems from the field were chosen for the purposes of a fleet analysis. Each system had at least one failure. All of the systems had a start time equal to zero and the last failure for each system corresponds to the end time. Group the data based on a fixed interval of 3000 hours and assume a fixed effectiveness factor equal to 0.4. Do the following:
1) Estimate the parameters of the Crow Extended model.
2) Based on the analysis does it appear that the systems were randomly ordered?
3) After the implementation of the delayed fixes, how many failures would you expect within the next 4000 hours of fleet operation.
| Table 13.9 - Fleet data for Example 5 | |
| System | Times-to-Failure |
|---|---|
| 1 | 1137 BD1, 1268 BD2 |
| 2 | 682 BD3, 744 A, 1336 BD1 |
| 3 | 95 BD1, 1593 BD3 |
| 4 | 1421 A |
| 5 | 1091 A, 1574 BD2 |
| 6 | 1415 BD4 |
| 7 | 598 BD4, 1290 BD1 |
| 8 | 1556 BD5 |
| 9 | 55 BD4 |
| 10 | 730 BD1, 1124 BD3 |
| 11 | 1400 BD4, 1568 A |
Solution to Example 5=
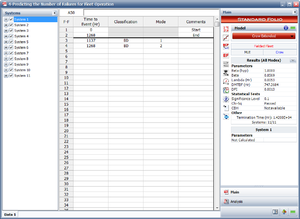
- 1) Figure Repair1 shows the estimated Crow Extended parameters.
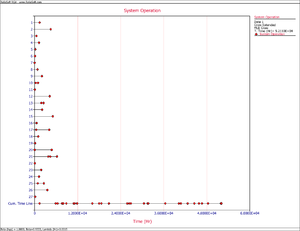
- 2) Upon observing the estimated parameter [math]\displaystyle{ \beta }[/math] it does appear that the systems were randomly ordered since [math]\displaystyle{ \beta =0.8569 }[/math] . This value is close to 1. You can also verify that the confidence bounds on [math]\displaystyle{ \beta }[/math] include 1 by going to the QCP and calculating the parameter bounds or by viewing the Beta Bounds plot. However, you can also determine graphically if the systems were randomly ordered by using the System Operation plot as shown in Figure Repair2. Looking at the Cum. Time Line, it does not appear that the failures have a trend associated with them. Therefore, the systems can be assumed to be randomly ordered.
[math]\displaystyle{ }[/math]
Fleet analysis is similar to the repairable systems analysis described in the previous chapter. The main difference is that a fleet of systems is considered and the models are applied to the fleet failures rather than to the system failures. In other words, repairable system analysis models the number of system failures versus system time; whereas fleet analysis models the number of fleet failures versus fleet time.
The main motivation for fleet analysis is to enable the application of the Crow Extended model for fielded data. In many cases, reliability improvements might be necessary on systems that are already in the field. These types of reliability improvements are essentially delayed fixes (BD modes) as described in Chapter 9.
Recall from the Crow Extended chapter that in order to make projections using the Crow Extended model, the [math]\displaystyle{ \beta }[/math] of the combined A and BD modes should be equal to 1. Since the failure intensity in a fielded system might be changing over time (e.g. increasing if the system wears out), this assumption might be violated. In such a scenario, the Crow Extended model cannot be used. However, if a fleet of systems is considered and the number of fleet failures versus fleet time is modeled, the failures might become random. This is because there is a mixture of systems within a fleet, new and old, and when the failures of this mixture of systems are viewed from a cumulative fleet time point of view, they may be random. Figures Repairable and Fleet illustrate this concept. Figure Repairable shows the number of failures over system age. It can be clearly seen that as the systems age, the intensity of the failures increases (wearout). The superposition system line, which brings the failures from the different systems under a single timeline, also illustrates this observation. On the other hand, if you take the same four systems and combine their failures from a fleet perspective, and consider fleet failures over cumulative fleet hours, then the failures seem to be random. Figure Fleet illustrates this concept in the System Operation plot when you consider the Cum. Time Line. In this case, the [math]\displaystyle{ \beta }[/math] of the fleet will be equal to 1 and the Crow Extended model can be used for quantifying the effects of future reliability improvements on the fleet.
Methodology
Figures Repairable and Fleet illustrate that the difference between repairable system data analysis and fleet analysis is the way that the dataset is treated. In fleet analysis, the time-to-failure data from each system is stacked to a cumulative timeline. For example, consider the two systems in Table 13.2.
| Table 13.2 - System data | ||
| System | Failure Times (hr) | End Time (hr) |
|---|---|---|
| 1 | 3, 7 | 10 |
| 2 | 4, 9, 13 | 15 |
The data set is first converted to an accumulated timeline, as follows:
- • System 1 is considered first. The accumulated timeline is therefore 3 and 7 hours.
- • System 1's End Time is 10 hours. System 2's first failure is at 4 hours. This failure time is added to System 1's End Time to give an accumulated failure time of 14 hours.
- • The second failure for System 2 occurred 5 hours after the first failure. This time interval is added to the accumulated timeline to give 19 hours.
- • The third failure for System 2 occurred 4 hours after the second failure. The accumulated failure time is 19 + 4 = 23 hours.
- • System 2's end time is 15 hours, or 2 hours after the last failure. The total accumulated operating time for the fleet is 25 hours (23 + 2 = 25).
In general, the accumulated operating time [math]\displaystyle{ {{Y}_{j}} }[/math] is calculated by:
- [math]\displaystyle{ {{Y}_{j}}={{X}_{i,q}}+\underset{q=1}{\overset{K-1}{\mathop \sum }}\,{{T}_{q}},\text{ }m=1,2,...,N }[/math]
- where:
- • [math]\displaystyle{ {{X}_{i,q}} }[/math] is the [math]\displaystyle{ {{i}^{th}} }[/math] failure of the [math]\displaystyle{ {{q}^{th}} }[/math] system
- • [math]\displaystyle{ {{T}_{q}} }[/math] is the end time of the [math]\displaystyle{ {{q}^{th}} }[/math] system
- • [math]\displaystyle{ K }[/math] is the total number of systems
- • [math]\displaystyle{ N }[/math] is the total number of failures from all systems ( [math]\displaystyle{ N=\underset{j=1}{\overset{K}{\mathop{\sum }}}\,{{N}_{q}} }[/math] )
As this example demonstrates, the accumulated timeline is determined based on the order of the systems. So if you consider the data in Table 13.2 by taking System 2 first, the accumulated timeline would be: 4, 9, 13, 18, 22, with an end time of 25. Therefore, the order in which the systems are considered is somewhat important. However, in the next step of the analysis the data from the accumulated timeline will be grouped into time intervals, effectively eliminating the importance of the order of the systems. Keep in mind that this will NOT always be true. This is true only when the order of the systems was random to begin with. If there is some logic/pattern in the order of the systems, then it will remain even if the cumulative timeline is converted to grouped data. For example, consider a system that wears out with age. This means that more failures will be observed as this system ages and these failures will occur more frequently. Within a fleet of such systems, there will be new and old systems in operation. If the dataset collected is considered from the newest to the oldest system, then even if the data points are grouped, the pattern of fewer failures at the beginning and more failures at later time intervals will still be present. If the objective of the analysis is to determine the difference between newer and older systems, then that order for the data will be acceptable. However, if the objective of the analysis is to determine the reliability of the fleet, then the systems should be randomly ordered.
Fleet Data Analysis
Once the accumulated timeline has been generated, it is then converted into grouped data. To accomplish this, a group interval is required. The group interval length should be chosen so that it is representative of the data. Also note that the intervals do not have to be of equal length. Once the data points have been grouped, the parameters can be obtained using maximum likelihood estimation as described in the Grouped Data Analysis section of the Crow-AMSAA (NHPP) chapter. The data from the table above can be grouped into 5 hour intervals. This interval length is sufficiently large to insure that there are failures within each interval. The grouped data set is given in the following table.
| Grouped data | |
| Failures in Interval | Interval End Time |
|---|---|
| 1 | 5 |
| 1 | 10 |
| 1 | 15 |
| 1 | 20 |
| 1 | 25 |
The Crow-AMSAA model for Grouped Failure Times is used for the data in Table 13.3 and the parameters of the model are solved by satisfying the following maximum likelihood equations (Chapter 5).
- [math]\displaystyle{ \begin{matrix} \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} \\ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i-1}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 \\ \end{matrix} }[/math]
Fleet Analysis Example
The following table presents data for a fleet of 27 systems. A cycle is a complete history from overhaul to overhaul. The failure history for the last completed cycle for each system is recorded. This is a random sample of data from the fleet. These systems are in the order in which they were selected. Suppose the intervals to group the current data are 10000, 20000, 30000, 40000 and the final interval is defined by the termination time. Conduct the fleet analysis.
| Sample fleet data | |||
| System | Cycle Time [math]\displaystyle{ {{T}_{j}} }[/math] | Number of failures [math]\displaystyle{ {{N}_{j}} }[/math] | Failure Time [math]\displaystyle{ {{X}_{ij}} }[/math] |
|---|---|---|---|
| 1 | 1396 | 1 | 1396 |
| 2 | 4497 | 1 | 4497 |
| 3 | 525 | 1 | 525 |
| 4 | 1232 | 1 | 1232 |
| 5 | 227 | 1 | 227 |
| 6 | 135 | 1 | 135 |
| 7 | 19 | 1 | 19 |
| 8 | 812 | 1 | 812 |
| 9 | 2024 | 1 | 2024 |
| 10 | 943 | 2 | 316, 943 |
| 11 | 60 | 1 | 60 |
| 12 | 4234 | 2 | 4233, 4234 |
| 13 | 2527 | 2 | 1877, 2527 |
| 14 | 2105 | 2 | 2074, 2105 |
| 15 | 5079 | 1 | 5079 |
| 16 | 577 | 2 | 546, 577 |
| 17 | 4085 | 2 | 453, 4085 |
| 18 | 1023 | 1 | 1023 |
| 19 | 161 | 1 | 161 |
| 20 | 4767 | 2 | 36, 4767 |
| 21 | 6228 | 3 | 3795, 4375, 6228 |
| 22 | 68 | 1 | 68 |
| 23 | 1830 | 1 | 1830 |
| 24 | 1241 | 1 | 1241 |
| 25 | 2573 | 2 | 871, 2573 |
| 26 | 3556 | 1 | 3556 |
| 27 | 186 | 1 | 186 |
| Total | 52110 | 37 | |
Solution
The sample fleet data set can be grouped into 10000, 20000, 30000, 4000 and 52110 time intervals. The following table gives the grouped data.
| Grouped data | |
| Time | Observed Failures |
|---|---|
| 10000 | 8 |
| 20000 | 16 |
| 30000 | 22 |
| 40000 | 27 |
| 52110 | 37 |
Based on the above time intervals, the maximum likelihood estimates of [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] for this data set are then given by:
- [math]\displaystyle{ \begin{matrix} \widehat{\lambda }=0.00147 \\ \widehat{\beta }=0.93328 \\ \end{matrix} }[/math]
The next figure shows the System Operation plot.
Template loop detected: Template:Applying the crow extended model to fleet data
Template loop detected: Template:Confidence bounds fleet rsa
General Examples
Predicting the Number of Failures for Fleet Operation
Eleven systems from the field were chosen for the purposes of a fleet analysis. Each system had at least one failure. All of the systems had a start time equal to zero and the last failure for each system corresponds to the end time. Group the data based on a fixed interval of 3000 hours and assume a fixed effectiveness factor equal to 0.4. Do the following:
1) Estimate the parameters of the Crow Extended model.
2) Based on the analysis does it appear that the systems were randomly ordered?
3) After the implementation of the delayed fixes, how many failures would you expect within the next 4000 hours of fleet operation.
| Table 13.9 - Fleet data for Example 5 | |
| System | Times-to-Failure |
|---|---|
| 1 | 1137 BD1, 1268 BD2 |
| 2 | 682 BD3, 744 A, 1336 BD1 |
| 3 | 95 BD1, 1593 BD3 |
| 4 | 1421 A |
| 5 | 1091 A, 1574 BD2 |
| 6 | 1415 BD4 |
| 7 | 598 BD4, 1290 BD1 |
| 8 | 1556 BD5 |
| 9 | 55 BD4 |
| 10 | 730 BD1, 1124 BD3 |
| 11 | 1400 BD4, 1568 A |
Solution to Example 5=
- 1) Figure Repair1 shows the estimated Crow Extended parameters.
- 2) Upon observing the estimated parameter [math]\displaystyle{ \beta }[/math] it does appear that the systems were randomly ordered since [math]\displaystyle{ \beta =0.8569 }[/math] . This value is close to 1. You can also verify that the confidence bounds on [math]\displaystyle{ \beta }[/math] include 1 by going to the QCP and calculating the parameter bounds or by viewing the Beta Bounds plot. However, you can also determine graphically if the systems were randomly ordered by using the System Operation plot as shown in Figure Repair2. Looking at the Cum. Time Line, it does not appear that the failures have a trend associated with them. Therefore, the systems can be assumed to be randomly ordered.
[math]\displaystyle{ }[/math]
General Examples
Predicting the Number of Failures for Fleet Operation
Eleven systems from the field were chosen for the purposes of a fleet analysis. Each system had at least one failure. All of the systems had a start time equal to zero and the last failure for each system corresponds to the end time. Group the data based on a fixed interval of 3000 hours and assume a fixed effectiveness factor equal to 0.4. Do the following:
1) Estimate the parameters of the Crow Extended model.
2) Based on the analysis does it appear that the systems were randomly ordered?
3) After the implementation of the delayed fixes, how many failures would you expect within the next 4000 hours of fleet operation.
| Table 13.9 - Fleet data for Example 5 | |
| System | Times-to-Failure |
|---|---|
| 1 | 1137 BD1, 1268 BD2 |
| 2 | 682 BD3, 744 A, 1336 BD1 |
| 3 | 95 BD1, 1593 BD3 |
| 4 | 1421 A |
| 5 | 1091 A, 1574 BD2 |
| 6 | 1415 BD4 |
| 7 | 598 BD4, 1290 BD1 |
| 8 | 1556 BD5 |
| 9 | 55 BD4 |
| 10 | 730 BD1, 1124 BD3 |
| 11 | 1400 BD4, 1568 A |
Solution to Example 5=
- 1) Figure Repair1 shows the estimated Crow Extended parameters.
- 2) Upon observing the estimated parameter [math]\displaystyle{ \beta }[/math] it does appear that the systems were randomly ordered since [math]\displaystyle{ \beta =0.8569 }[/math] . This value is close to 1. You can also verify that the confidence bounds on [math]\displaystyle{ \beta }[/math] include 1 by going to the QCP and calculating the parameter bounds or by viewing the Beta Bounds plot. However, you can also determine graphically if the systems were randomly ordered by using the System Operation plot as shown in Figure Repair2. Looking at the Cum. Time Line, it does not appear that the failures have a trend associated with them. Therefore, the systems can be assumed to be randomly ordered.
[math]\displaystyle{ }[/math]