|
|
| (45 intermediate revisions by 7 users not shown) |
| Line 1: |
Line 1: |
| =Temperature-Humidity Relationship=
| | {{template:ALTABOOK|9}} |
| | So far in this reference the life-stress relationships presented have been either single stress relationships or two stress relationships. In most practical applications, however, life is a function of more than one or two variables (stress types). In addition, there are many applications where the life of a product as a function of stress and of some engineering variable other than stress is sought. In this chapter, the general log-linear relationship and the proportional hazards model are presented for the analysis of such cases where more than two accelerated stresses (or variables) need to be considered. |
| <br> | | <br> |
|
| |
|
| ==Introduction== | | =General Log-Linear Relationship= |
| <br>
| | {{:General Log-Linear Relationship}} |
| | |
| The Temperature-Humidity (T-H) relationship, a variation of the Eyring relationship, has been proposed for predicting the life at use conditions when temperature and humidity are the accelerated stresses in a test. This combination model is given by:
| |
| | |
| <br>
| |
| | |
| ::<math>L(V,U)=A{{e}^{\tfrac{\phi }{V}+\tfrac{b}{U}}}</math>
| |
| <br>
| |
| | |
| where:
| |
| <br>
| |
| • <math>\phi </math> is one of the three parameters to be determined.
| |
| • <math>b</math> is the second of the three parameters to be determined (also known as the activation energy for humidity).
| |
| • <math>A</math> is a constant and the third of the three parameters to be determined.
| |
| • <math>U</math> is the relative humidity (decimal or percentage).
| |
| • <math>V</math> is temperature (in absolute units ).
| |
| <br>
| |
| | |
| The T-H relationship can be linearized and plotted on a Life vs. Stress plot. The relationship is linearized by taking the natural logarithm of both sides in Eqn. (Temp-Hum), or:
| |
| | |
| <br>
| |
| ::<math>ln(L(V,U))=ln(A)+\frac{\phi }{V}+\frac{b}{U}</math>
| |
| | |
| <br>
| |
| Since life is now a function of two stresses, a Life vs. Stress plot can only be obtained by keeping one of the two stresses constant and varying the other one. Doing so will yield a straight line as described by Eqn. (ln Temp-Hum), where the term for the stress which is kept at a fixed value becomes another constant (in addition to the <math>\ln (A)</math> constant). In Figs. 1 and 2, data obtained from a temperature and humidity test were analyzed and plotted on Arrhenius paper. In Fig. 1, life is plotted versus temperature with relative humidity held at a fixed value. In Fig. 2, life is plotted versus relative humidity with temperature held at a fixed value.
| |
| <br>
| |
| [[File:ALTA9.1.gif|center]]
| |
| <br>
| |
| ::Fig. 1: Life vs. Temperature plot at a fixed relative humidity.
| |
| <br>
| |
| | |
| <math></math>
| |
| <br>
| |
| [[File:ALTA9.2.gif|center]]
| |
| <br>
| |
| ::Fig. 2: Life vs. Relative Humidity plot at a fixed temperature.
| |
| <br>
| |
| Note that the Life vs. Stress plots in both Figs. 1 and 2 are plotted on a log-reciprocal scale. Also note that the points shown in these plots represent the life characteristics at the test stress levels (the data set was fitted to a Weibull distribution, thus the points represent the scale parameter, <math>\eta )</math> . For example, the points shown in Fig. 1 represent <math>\eta </math> at each of the test temperature levels (two temperature levels were considered in this test).
| |
| <br>
| |
| | |
| ==A look at the Parameters <math>\phi </math> and <math>b</math>==
| |
| <br>
| |
| Depending on which stress type is kept constant, it can be seen from Eqn. (ln Temp-Hum) that either the parameter <math>\phi </math> or the parameter <math>b</math> is the slope of the resulting line. If, for example, the humidity is kept constant (Fig. 1) then <math>\phi </math> is the slope of the life line in a Life vs. Temperature plot. The steeper the slope, the greater the dependency of product life to the temperature. In other words, <math>\phi </math> is a measure of the effect that temperature has on the life, and <math>b</math> is a measure of the effect that relative humidity has on the life. The larger the value of <math>\phi ,</math> the higher the dependency of the life on the temperature. Similarly, the larger the value of <math>b,</math> the higher the dependency of the life on the humidity. For example, it can be seen by comparing Figs. 1 and 2 that, for this data set, temperature has a greater effect on the life than humidity.
| |
| <br>
| |
| ==T-H Data==
| |
| <br>
| |
| When using the T-H relationship, the effect of both temperature and humidity on life is sought. For this reason, the test must be performed in a combination manner between the different stress levels of the two stress types. For example, assume that an accelerated test is to be performed at two temperature and two humidity levels. The two temperature levels were chosen to be 300K and 343K. The two humidity levels were chosen to be 0.6 and 0.8. It would be wrong to perform the test at (300K, 0.6) and (343K, 0.8). Doing so would not provide information about the temperature-humidity effects on life. This is because both stresses are increased at the same time and therefore it is unknown which stress is causing the acceleration on life. A possible combination that would provide information about temperature-humidity effects on life would be (300K, 0.6), (300K, 0.8) and (343K, 0.8). It is clear that by testing at (300K, 0.6) and (300K, 0.8) the effect of humidity on life can be determined (since temperature remained constant). Similarly the effects of temperature on life can be determined by testing at (300K, 0.8) and (343K, 0.8) since humidity remained constant.
| |
| <br>
| |
| <br>
| |
| ==Acceleration Factor==
| |
| <br>
| |
| The acceleration factor for the T-H relationship is given by:
| |
| | |
| | |
| <br>
| |
| ::<math>{{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}}=\frac{A{{e}^{\tfrac{\phi }{{{V}_{u}}}+\tfrac{b}{{{U}_{u}}}}}}{A{{e}^{\tfrac{\phi }{{{V}_{A}}}+\tfrac{b}{{{U}_{A}}}}}}={{e}^{\phi \left( \tfrac{1}{{{V}_{u}}}-\tfrac{1}{{{V}_{A}}} \right)+b\left( \tfrac{1}{{{U}_{u}}}-\tfrac{1}{{{U}_{A}}} \right)}}</math>
| |
| | |
| <br>
| |
| where:
| |
| <br>
| |
| • <math>{{L}_{USE}}</math> is the life at use stress level.
| |
| • <math>{{L}_{Accelerated}}</math> is the life at the accelerated stress level.
| |
| • <math>{{V}_{u}}</math> is the use temperature level.
| |
| • <math>{{V}_{A}}</math> is the accelerated temperature level.
| |
| • <math>{{U}_{A}}</math> is the accelerated humidity level.
| |
| • <math>{{U}_{u}}</math> is the use humidity level.
| |
| <br>
| |
| The acceleration Factor is plotted versus stress in the same manner used to create the Life vs. Stress plots. That is, one stress type is kept constant and the other is varied (see Figs. 3 and 4).
| |
| <br>
| |
| [[File:ALTA9.3.gif|center]]
| |
| <br>
| |
| ::Fig. 3: Acceleration Factor vs. Temperature at a fixed relative humidity.
| |
| <br>
| |
| [[File:ALTA9.4.gif|center]]
| |
| <br>
| |
| ::Fig. 4: Acceleration Factor vs. Humidity at a fixed temperature.
| |
| <br>
| |
| | |
| ==T-H Exponential==
| |
| <br>
| |
| By setting <math>m=L(U,V)</math> in Eqn. (Temp-Hum) the exponential <math>pdf</math> becomes:
| |
| | |
| <br>
| |
| ::<math>f(t,V,U)=\frac{1}{A}{{e}^{-\left( \tfrac{\phi }{V}+\tfrac{b}{U} \right)}}\cdot {{e}^{-\tfrac{t}{A}\cdot {{e}^{-\left( \tfrac{\phi }{V}+\tfrac{b}{U} \right)}}}}</math>
| |
| | |
| <br>
| |
| ===T-H Exponential Statistical Properties Summary===
| |
| <br>
| |
| ====Mean or MTTF====
| |
| <br>
| |
| The mean, <math>\overline{T},</math> or Mean Time To Failure (MTTF) for the T-H exponential model is given by:
| |
| | |
| <br>
| |
| ::<math>\overline{T}=\mathop{}_{0}^{\infty }t\cdot f(t,V,U)dt</math>
| |
| | |
| <br>
| |
| Substituting Eqn. (t-h exp pdf) yields:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & \overline{T}= & \mathop{}_{0}^{\infty }t\cdot \frac{1}{A}{{e}^{-\left( \tfrac{\phi }{V}+\tfrac{b}{U} \right)}}{{e}^{-\tfrac{t}{A}{{e}^{-\left( \tfrac{\phi }{V}+\tfrac{b}{U} \right)}}}}dt \\
| |
| & = & A{{e}^{\tfrac{\phi }{V}+\tfrac{b}{U}}}
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| ====Median====
| |
| <br>
| |
| The median, <math>\breve{T},</math> for the T-H exponential model is given by:
| |
| | |
| <br>
| |
| ::<math>\breve{T}=0.693\cdot A{{e}^{\tfrac{\phi }{V}+\tfrac{b}{U}}}</math>
| |
| | |
| <br>
| |
| | |
| ====Mode====
| |
| <br>
| |
| The mode, <math>\tilde{T},</math> for the T-H exponential model is given by:
| |
| | |
| <br>
| |
| ::<math>\tilde{T}=0</math>
| |
| | |
| ====Standard Deviation====
| |
| <br>
| |
| The standard deviation, <math>{{\sigma }_{T}}</math> , for the T-H exponential model is given by:
| |
| | |
| <br>
| |
| ::<math>{{\sigma }_{T}}=A{{e}^{\tfrac{\phi }{V}+\tfrac{b}{U}}}</math>
| |
| | |
| ====T-H Exponential Reliability Function====
| |
| <br>
| |
| The T-H exponential reliability function is given by:
| |
| | |
| <br>
| |
| ::<math>R(T,V,U)={{e}^{-\tfrac{T}{A}{{e}^{-\left( \tfrac{\phi }{V}+\tfrac{b}{U} \right)}}}}</math>
| |
| | |
| <br>
| |
| This function is the complement of the T-H exponential cumulative distribution function or:
| |
| | |
| <br>
| |
| ::<math>R(T,V,U)=1-Q(T,V,U)=1-\mathop{}_{0}^{T}f(T)dT</math>
| |
| | |
| <br>
| |
| and:
| |
| | |
| | |
| <br>
| |
| ::<math>R(T,V,U)=1-\mathop{}_{0}^{T}\frac{1}{A}{{e}^{-\left( \tfrac{\phi }{V}+\tfrac{b}{U} \right)}}{{e}^{-\tfrac{T}{A}{{e}^{-\left( \tfrac{\phi }{V}+\tfrac{b}{U} \right)}}}}dT={{e}^{-\tfrac{T}{A}{{e}^{-\left( \tfrac{\phi }{V}+\tfrac{b}{U} \right)}}}}</math>
| |
| | |
| <br>
| |
| ====Conditional Reliability====
| |
| <br>
| |
| The conditional reliability function for the T-H exponential model is given by:
| |
| | |
| <br>
| |
| ::<math>R(T,t,V,U)=\frac{R(T+t,V,U)}{R(T,V,U)}=\frac{{{e}^{-\lambda (T+t)}}}{{{e}^{-\lambda T}}}={{e}^{-\tfrac{t}{A}{{e}^{-\left( \tfrac{\phi }{V}+\tfrac{b}{U} \right)}}}}</math>
| |
| | |
| <br>
| |
| ====Reliable Life====
| |
| <br>
| |
| For the T-H exponential model, the reliable life, or the mission duration for a desired reliability goal, <math>{{t}_{R}},</math> is given by:
| |
| | |
| <br>
| |
| ::<math>R({{t}_{R}},V,U)={{e}^{-\tfrac{{{t}_{R}}}{A}{{e}^{-\left( \tfrac{\phi }{V}+\tfrac{b}{U} \right)}}}}</math>
| |
| | |
| <br>
| |
| ::<math>\ln [R({{t}_{R}},V,U)]=-\frac{{{t}_{R}}}{A}{{e}^{-\left( \tfrac{\phi }{V}+\tfrac{b}{U} \right)}}</math>
| |
| | |
| <br>
| |
| or:
| |
| | |
| <br>
| |
| ::<math>{{t}_{R}}=-A{{e}^{\tfrac{\phi }{V}+\tfrac{b}{U}}}\ln [R({{t}_{R}},V,U)]</math>
| |
| | |
| <br>
| |
| ===Parameter Estimation===
| |
| <br>
| |
| ====Maximum Likelihood Estimation Method====
| |
| <br>
| |
| Substituting the T-H model into the exponential log-likelihood equation yields:
| |
| | |
| <br>
| |
| ::<math>\begin{align} | |
| & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{1}{A}{{e}^{-\left( \tfrac{\phi }{{{V}_{i}}}+\tfrac{b}{{{U}_{i}}} \right)}}\cdot {{e}^{-\tfrac{{{T}_{i}}}{A}\cdot {{e}^{-\left( \tfrac{\phi }{{{V}_{i}}}+\tfrac{b}{{{U}_{i}}} \right)}}}} \right] \\
| |
| & & -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{T_{i}^{\prime }}{A}{{e}^{-\left( \tfrac{\phi }{{{V}_{i}}}+\tfrac{b}{{{U}_{i}}} \right)}}+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }]
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| where:
| |
| | |
| <br>
| |
| ::<math>R_{Li}^{\prime \prime }={{e}^{-\tfrac{T_{Li}^{\prime \prime }}{A}{{e}^{-\left( \tfrac{\phi }{{{V}_{i}}}+\tfrac{b}{U_{i}^{\prime \prime }} \right)}}}}</math>
| |
| | |
| <br>
| |
| ::<math>R_{Ri}^{\prime \prime }={{e}^{-\tfrac{T_{Ri}^{\prime \prime }}{A}{{e}^{-\left( \tfrac{\phi }{{{V}_{i}}}+\tfrac{b}{U_{i}^{\prime \prime }} \right)}}}}</math>
| |
| | |
| <br>
| |
| and:
| |
| <br>
| |
| • <math>{{F}_{e}}</math> is the number of groups of exact times-to-failure data points.
| |
| <br>
| |
| • <math>{{N}_{i}}</math> is the number of times-to-failure data points in the <math>{{i}^{th}}</math> time-to-failure data group.
| |
| <br>
| |
| • <math>A</math> is the T-H parameter (unknown, the first of three parameters to be estimated).
| |
| <br>
| |
| • <math>\phi </math> is the second T-H parameter (unknown, the second of three parameters to be estimated).
| |
| <br>
| |
| • <math>b</math> is the third T-H parameter (unknown, the third of three parameters to be estimated).
| |
| <br>
| |
| • <math>{{V}_{i}}</math> is the temperature level of the <math>{{i}^{th}}</math> group.
| |
| <br>
| |
| • <math>{{U}_{i}}</math> is the relative humidity level of the <math>{{i}^{th}}</math> group.
| |
| <br>
| |
| • <math>{{T}_{i}}</math> is the exact failure time of the <math>{{i}^{th}}</math> group.
| |
| <br>
| |
| • <math>S</math> is the number of groups of suspension data points.
| |
| <br>
| |
| • .. is the number of suspensions in the <math>{{i}^{th}}</math> group of suspension data points.
| |
| <br>
| |
| • <math>T_{i}^{\prime }</math> is the running time of the <math>{{i}^{th}}</math> suspension data group.
| |
| <br>
| |
| • <math>FI</math> is the number of interval data groups.
| |
| <br>
| |
| • <math>N_{i}^{\prime \prime }</math> is the number of intervals in the <math>{{i}^{th}}</math> group of data intervals.
| |
| <br>
| |
| • <math>T_{Li}^{\prime \prime }</math> is the beginning of the <math>{{i}^{th}}</math> interval.
| |
| <br>
| |
| • <math>T_{Ri}^{\prime \prime }</math> is the ending of the <math>{{i}^{th}}</math> interval.
| |
| <br>
| |
| <br>
| |
| The solution (parameter estimates) will be found by solving for the parameters <math>A,</math> <math>\phi </math> and <math>b</math> so that <math>\tfrac{\partial \Lambda }{\partial A}=0,</math> <math>\tfrac{\partial \Lambda }{\partial \phi }=0</math> and <math>\tfrac{\partial \Lambda }{\partial b}=0</math> .
| |
| | |
| ==T-H Weibull==
| |
| <br>
| |
| By setting <math>\eta =L(U,V)</math> as given in Eqn. (Temp-Hum), the T--H Weibull model's <math>pdf</math> is given by:
| |
| ..
| |
| | |
| <br>
| |
| ===T-H Weibull Statistical Properties Summary===
| |
| <br>
| |
| ====Mean or MTTF====
| |
| <br>
| |
| The mean, <math>\overline{T}</math> (also called <math>MTTF</math> ), of the T-H Weibull model is given by:
| |
|
| |
|
| <br>
| | =Proportional Hazards Model= |
| ::<math>\overline{T}=A{{e}^{\tfrac{\phi }{V}+\tfrac{b}{U}}}\cdot \Gamma \left( \frac{1}{\beta }+1 \right)</math>
| | {{:Proportional Hazards Model}} |
| | |
| <br>
| |
| where <math>\Gamma \left( \tfrac{1}{\beta }+1 \right)</math> is the gamma function evaluated at the value of <math>\left( \tfrac{1}{\beta }+1 \right)</math> .
| |
| <br>
| |
| ====Median====
| |
| <br>
| |
| The median, <math>\breve{T},</math> of the T-H Weibull model is given by:
| |
| | |
| <br>
| |
| ::<math>\breve{T}=A{{e}^{\tfrac{\phi }{V}+\tfrac{b}{U}}}{{\left( \ln 2 \right)}^{\tfrac{1}{\beta }}}</math>
| |
|
| |
|
| ====Mode==== | | =Indicator Variables= |
| <br>
| | Another advantage of the multivariable relationships included in ALTA is that they allow for simultaneous analysis of continuous and categorical variables. Categorical variables are variables that take on discrete values such as the lot designation for products from different manufacturing lots. In this example, lot is a categorical variable, and it can be expressed in terms of indicator variables. Indicator variables only take a value of 1 or 0. For example, consider a sample of test units. A number of these units were obtained from Lot 1, others from Lot 2, and the rest from Lot 3. These three lots can be represented with the use of indicator variables, as follows: |
| The mode, <math>\tilde{T},</math> of the T-H Weibull model is given by:
| |
|
| |
|
| <br>
| | *Define two indicator variables, <math>{{X}_{1}}\,\!</math> and <math>{{X}_{2}}.\,\!</math> |
| ::<math>\tilde{T}=A{{e}^{\tfrac{\phi }{V}+\tfrac{b}{U}}}{{\left( 1-\frac{1}{\beta } \right)}^{\tfrac{1}{\beta }}}</math>
| |
| <br>
| |
|
| |
|
| ====Standard Deviation==== | | *For the units from Lot 1, <math>{{X}_{1}}=1,\,\!</math> and <math>{{X}_{2}}=0.\,\!</math> |
| <br> | |
| The standard deviation, <math>{{\sigma }_{T}},</math> of the T-H Weibull model is given by:
| |
|
| |
|
| <br>
| | *For the units from Lot 2, <math>{{X}_{1}}=0,\,\!</math> and <math>{{X}_{2}}=1.\,\!</math> |
| ::<math>{{\sigma }_{T}}=A{{e}^{\tfrac{\phi }{V}+\tfrac{b}{U}}}\cdot \sqrt{\Gamma \left( \frac{2}{\beta }+1 \right)-{{\left( \Gamma \left( \frac{1}{\beta }+1 \right) \right)}^{2}}}</math>
| |
|
| |
|
| <br> | | *For the units from Lot 3, <math>{{X}_{1}}=0,\,\!</math> and <math>{{X}_{2}}=0.\,\!</math> |
| ====T-H Weibull Reliability Function====
| |
| <br> | |
| The T-H Weibull reliability function is given by:
| |
|
| |
|
| <br>
| | Assume that an accelerated test was performed with these units, and temperature was the accelerated stress. In this case, the GLL relationship can be used to analyze the data. From the GLL relationship we get: |
| ::<math>R(T,V,U)={{e}^{-{{\left( \tfrac{T}{A}{{e}^{-\left( \tfrac{\phi }{V}+\tfrac{b}{U} \right)}} \right)}^{\beta }}}}</math>
| |
|
| |
|
| ====Conditional Reliability Function==== | | ::<math>L(\underline{X})={{e}^{{{\alpha }_{0}}+{{\alpha }_{1}}{{X}_{1}}+{{\alpha }_{2}}{{X}_{2}}+{{\alpha }_{3}}{{X}_{3}}}}\,\!</math> |
| <br> | |
| The T-H Weibull conditional reliability function at a specified stress level is given by:
| |
|
| |
|
| <br>
| |
| ::<math>R(T,t,V,U)=\frac{R(T+t,V,U)}{R(T,V,U)}=\frac{{{e}^{-{{\left( \tfrac{T+t}{A}{{e}^{-\left( \tfrac{\phi }{V}+\tfrac{b}{U} \right)}} \right)}^{\beta }}}}}{{{e}^{-{{\left( \tfrac{T}{A}{{e}^{-\left( \tfrac{\phi }{V}+\tfrac{b}{U} \right)}} \right)}^{\beta }}}}}</math>
| |
|
| |
| <br>
| |
| or:
| |
|
| |
| <br>
| |
| ::<math>R(T,t,V,U)={{e}^{-\left[ {{\left( \tfrac{T+t}{A}{{e}^{-\left( \tfrac{\phi }{V}+\tfrac{b}{U} \right)}} \right)}^{\beta }}-{{\left( \tfrac{T}{A}{{e}^{-\left( \tfrac{\phi }{V}+\tfrac{b}{U} \right)}} \right)}^{\beta }} \right]}}</math>
| |
|
| |
| <br>
| |
| ====Reliable Life====
| |
| <br>
| |
| For the T-H Weibull model, the reliable life, <math>{{t}_{R}}</math> , of a unit for a specified reliability and starting the mission at age zero is given by:
| |
|
| |
| <br>
| |
| ::<math>{{t}_{R}}=A{{e}^{\tfrac{\phi }{V}+\tfrac{b}{U}}}{{\left\{ -\ln \left[ R\left( {{T}_{R}},V,U \right) \right] \right\}}^{\tfrac{1}{\beta }}}</math>
| |
|
| |
| <br>
| |
| ====T-H Weibull Failure Rate Function====
| |
| <br>
| |
| The T-H Weibull failure rate function, <math>\lambda (T,V,U)</math> , is given by:
| |
|
| |
| <br>
| |
| ::<math>\lambda \left( T,V,U \right)=\frac{f\left( T,V,U \right)}{R\left( T,V,U \right)}=\frac{\beta }{A}{{e}^{-\left( \tfrac{\phi }{V}+\tfrac{b}{U} \right)}}{{\left( \frac{T}{A}{{e}^{-\left( \tfrac{\phi }{V}+\tfrac{b}{U} \right)}} \right)}^{\beta -1}}</math>
| |
|
| |
| <br>
| |
| ===Parameter Estimation===
| |
| <br>
| |
| ====Maximum Likelihood Estimation Method====
| |
| <br>
| |
| Substituting the T-H model into the Weibull log-likelihood function yields:
| |
|
| |
| <br>
| |
| ::<math>\begin{align}
| |
| & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{\beta }{A}{{e}^{-\left( \tfrac{\phi }{{{V}_{i}}}+\tfrac{b}{{{U}_{i}}} \right)}}{{\left( \frac{{{T}_{i}}}{A}{{e}^{-\left( \tfrac{\phi }{{{V}_{i}}}+\tfrac{b}{{{U}_{i}}} \right)}} \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{{{T}_{i}}}{A}{{e}^{-\left( \tfrac{\phi }{{{V}_{i}}}+\tfrac{b}{{{U}_{i}}} \right)}} \right)}^{\beta }}}} \right] \\
| |
| & & -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }{{\left( \frac{T_{i}^{\prime }}{A}{{e}^{-\left( \tfrac{\phi }{{{V}_{i}}}+\tfrac{b}{{{U}_{i}}} \right)}} \right)}^{\beta }}+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }]
| |
| \end{align}</math>
| |
|
| |
| <br>
| |
| where: | | where: |
|
| |
|
| <br>
| | *<math>{{X}_{1}}\,\!</math> and <math>{{X}_{2}}\,\!</math> are the indicator variables, as defined above. |
| ::<math>R_{Li}^{\prime \prime }={{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }}{A}{{e}^{-\left( \tfrac{\phi }{{{V}_{i}}}+\tfrac{b}{U_{i}^{\prime \prime }} \right)}} \right)}^{\beta }}}}</math>
| |
| | |
| <br>
| |
| ::<math>R_{Ri}^{\prime \prime }={{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }}{A}{{e}^{-\left( \tfrac{\phi }{{{V}_{i}}}+\tfrac{b}{U_{i}^{\prime \prime }} \right)}} \right)}^{\beta }}}}</math>
| |
|
| |
|
| <br>
| | *<math>{{X}_{3}}=\tfrac{1}{T},\,\!</math> where <math>T\,\!</math> is the temperature. |
| and:
| |
| <br>
| |
| • <math>{{F}_{e}}</math> is the number of groups of exact times-to-failure data points.
| |
| <br>
| |
| • <math>{{N}_{i}}</math> is the number of times-to-failure data points in the <math>{{i}^{th}}</math> time-to-failure data group.
| |
| <br>
| |
| • <math>\beta </math> is the Weibull shape parameter (unknown, the first of four parameters to be estimated).
| |
| <br>
| |
| • .. is the T-H parameter (unknown, the second of four parameters to be estimated).
| |
| <br>
| |
| • <math>\phi </math> is the second T-H parameter (unknown, the third of four parameters to be estimated).
| |
| <br>
| |
| • <math>b</math> is the third T-H parameter (unknown, the fourth of four parameters to be estimated).
| |
| <br>
| |
| • <math>{{V}_{i}}</math> is the temperature level of the <math>{{i}^{th}}</math> group.
| |
| <br>
| |
| • <math>{{U}_{i}}</math> is the relative humidity level of the <math>{{i}^{th}}</math> group.
| |
| <br>
| |
| • <math>{{T}_{i}}</math> is the exact failure time of the <math>{{i}^{th}}</math> group.
| |
| <br>
| |
| • <math>S</math> is the number of groups of suspension data points.
| |
| <br>
| |
| • <math>N_{i}^{\prime }</math> is the number of suspensions in the <math>{{i}^{th}}</math> group of suspension data points.
| |
| <br>
| |
| • <math>T_{i}^{\prime }</math> is the running time of the <math>{{i}^{th}}</math> suspension data group.
| |
| <br>
| |
| • <math>FI</math> is the number of interval data groups.
| |
| <br>
| |
| • <math>N_{i}^{\prime \prime }</math> is the number of intervals in the <math>{{i}^{th}}</math> group of data intervals.
| |
| <br>
| |
| • <math>T_{Li}^{\prime \prime }</math> is the beginning of the interval.
| |
| <br>
| |
| • <math>T_{Ri}^{\prime \prime }</math> is the ending of the <math>{{i}^{th}}</math> interval.
| |
| <br>
| |
| The solution (parameter estimates) will be found by solving for the parameters <math>A,</math> <math>\phi ,</math> <math>b</math> and <math>\beta </math> so that <math>\tfrac{\partial \Lambda }{\partial \beta }=0,</math> <math>\tfrac{\partial \Lambda }{\partial A}=0,</math> <math>\tfrac{\partial \Lambda }{\partial \phi }=0</math> and <math>\tfrac{\partial \Lambda }{\partial b}=0</math> .
| |
| <br>
| |
| <br>
| |
|
| |
|
| ===Example===
| | The data can now be entered in ALTA and, with the assumption of an underlying life distribution and using MLE, the parameters of this model can be obtained. |
| <br>
| |
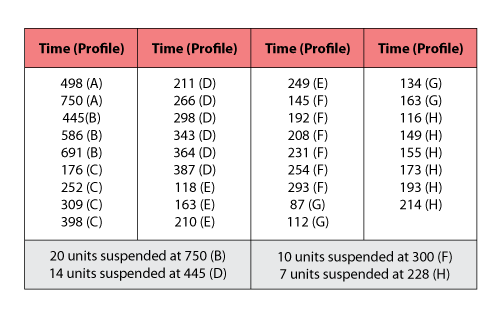
| The following data were collected after testing twelve electronic devices at different temperature and humidity conditions: | |
| <br>
| |
| <br>
| |
| [[File:ex1chp9.gif|center|center]]
| |
| <br>
| |
| <br>
| |
| Using ALTA, the following results were obtained:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & \widehat{\beta }= & 5.87439512 \\
| |
| & & \\
| |
| & \widehat{A}= & 0.0000597 \\
| |
| & & \\
| |
| & \widehat{b}= & 0.2805985 \\
| |
| & & \\
| |
| & \widehat{\phi }= & 5630.329851
| |
| \end{align}</math>
| |
| | |
| <br>
| |
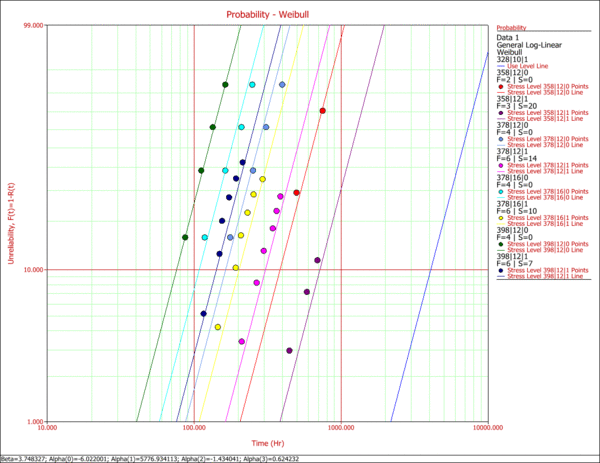
| A probability plot for the entered data is shown next.
| |
| | |
| <br>
| |
| [[File:ALTA9probabilityplot.gif|center]]
| |
| <br>
| |
| ::Fig. 5: Probability plots at the tested combinations.
| |
| <br>
| |
| <br>
| |
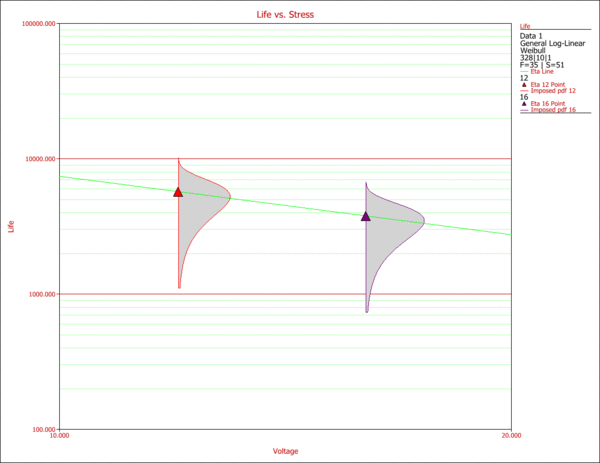
| Note that three lines are plotted because there are three combinations of stresses, namely, (398K, 0.4), (378K, 0.8) and (378K, 0.4).
| |
| | |
| <br>
| |
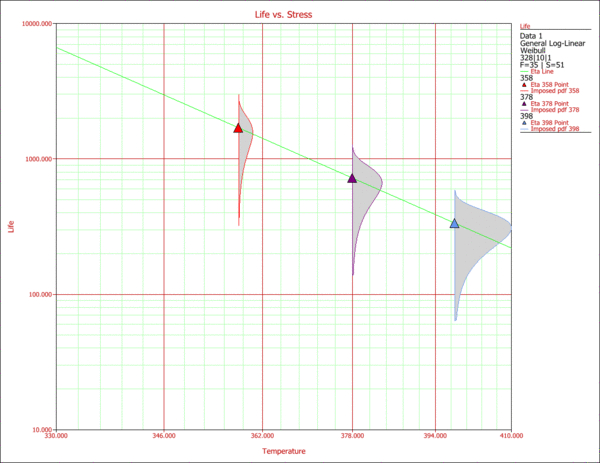
| Given the use stress levels, time estimates can be obtained for specified probability. A Life vs. Stress plot can be obtained if one of the stresses is kept constant. For example, the following picture is a Life vs. Humidity plot at a constant temperature of 338K.
| |
| <br>
| |
| [[File:ALTA9stressplot.gif|center]]
| |
| <br>
| |
| ::Fig. 6: Life vs. Humidity plot with temperature fixed at 338K.
| |
| <br>
| |
| | |
| ==T-H Lognormal==
| |
| <br>
| |
| The <math>pdf</math> of the lognormal distribution is given by:
| |
| <br>
| |
| | |
| ::<math>f(T)=\frac{1}{T\text{ }{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{T}'-\overline{{{T}'}}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}}</math>
| |
| | |
| <br>
| |
| where:
| |
| | |
| <br>
| |
| ::<math>{T}'=\ln (T)</math>
| |
| | |
| <br>
| |
| ::<math>T=\text{times-to-failure}</math>
| |
| | |
| <br>
| |
| and:
| |
| <br>
| |
| • <math>\overline{{{T}'}}=</math> mean of the natural logarithms of the times-to-failure.
| |
| • <math>{{\sigma }_{{{T}'}}}=</math> standard deviation of the natural logarithms of the times-to-failure.
| |
| <br>
| |
| The median of the lognormal distribution is given by:
| |
| | |
| <br>
| |
| ::<math>\breve{T}={{e}^{{{\overline{T}}^{\prime }}}}</math>
| |
| | |
| <br>
| |
| The T-H lognormal model <math>pdf</math> can be obtained first by setting <math>\breve{T} =L(V,U)</math> in Eqn. (Temp-Hum). <br>
| |
| Therefore:
| |
| | |
| | |
| <br>
| |
| ::<math>\breve{T}=L(V,U)=A{{e}^{\tfrac{\phi }{V}+\tfrac{b}{U}}}</math>
| |
| | |
| <br>
| |
| or:
| |
| <br>
| |
| ::<math>{{e}^{{{\overline{T}}^{\prime }}}}=A{{e}^{\tfrac{\phi }{V}+\tfrac{b}{U}}}</math>
| |
| | |
| <br>
| |
| Thus:
| |
| <br>
| |
| ::<math>{{\overline{T}}^{\prime }}=\ln (A)+\frac{\phi }{V}+\frac{b}{U}.</math>
| |
| | |
| <br>
| |
| Substituting Eqn. (TH-logn-mean) into Eqn. (TH-logn-pdf) yields the T-H lognormal model <math>pdf</math> or:
| |
| | |
| <br>
| |
| ::<math>f(T,V,U)=\frac{1}{T\text{ }{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{T}'-\ln (A)-\tfrac{\phi }{V}-\tfrac{b}{U}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}}</math>
| |
| | |
| <br>
| |
| ===T-H Lognormal Statistical Properties Summary===
| |
| <br>
| |
| ====The Mean====
| |
| <br>
| |
| • The mean life of the T-H lognormal model (mean of the times-to-failure), <math>\bar{T}</math> , is given by:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & \bar{T}= & {{e}^{\bar{{T}'}+\tfrac{1}{2}\sigma _{{{T}'}}^{2}}} \\
| |
| & = & {{e}^{\ln (A)+\tfrac{\phi }{V}+\tfrac{b}{U}+\tfrac{1}{2}\sigma _{{{T}'}}^{2}}}
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| • The mean of the natural logarithms of the times-to-failure, <math>{{\bar{T}}^{^{\prime }}}</math> , in terms of <math>\bar{T}</math> and <math>{{\sigma }_{T}}</math> is given by:
| |
| | |
| <br>
| |
| ::<math>{{\bar{T}}^{\prime }}=\ln \left( {\bar{T}} \right)-\frac{1}{2}\ln \left( \frac{\sigma _{T}^{2}}{{{{\bar{T}}}^{2}}}+1 \right)</math>
| |
| | |
| <br>
| |
| ====The Standard Deviation====
| |
| <br>
| |
| • The standard deviation of the T-H lognormal model (standard deviation of the times-to-failure), <math>{{\sigma }_{T}}</math> , is given by:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & {{\sigma }_{T}}= & \sqrt{\left( {{e}^{2\bar{{T}'}+\sigma _{{{T}'}}^{2}}} \right)\left( {{e}^{\sigma _{{{T}'}}^{2}}}-1 \right)} \\
| |
| & = & \sqrt{\left( {{e}^{2\left( \ln (A)+\tfrac{\phi }{V}+\tfrac{b}{U} \right)+\sigma _{{{T}'}}^{2}}} \right)\left( {{e}^{\sigma _{{{T}'}}^{2}}}-1 \right)}
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| • The standard deviation of the natural logarithms of the times-to-failure, <math>{{\sigma }_{{{T}'}}}</math> , in terms of <math>\bar{T}</math> and <math>{{\sigma }_{T}}</math> is given by:
| |
| | |
| <br>
| |
| ::<math>{{\sigma }_{{{T}'}}}=\sqrt{\ln \left( \frac{\sigma _{T}^{2}}{{{{\bar{T}}}^{2}}}+1 \right)}</math>
| |
| | |
| <br>
| |
| ====The Mode====
| |
| <br>
| |
| • The mode of the T-H lognormal model is given by:
| |
|
| |
| <math>\begin{align}
| |
| & \tilde{T}= & {{e}^{{{\overline{T}}^{\prime }}-\sigma _{{{T}'}}^{2}}} \\
| |
| & = & {{e}^{\ln (A)+\tfrac{\phi }{V}+\tfrac{b}{U}-\sigma _{{{T}'}}^{2}}}
| |
| \end{align}</math>
| |
|
| |
|
| |
| <br>
| |
| ====T-H Lognormal Reliability====
| |
| <br>
| |
| The reliability for a mission of time <math>T</math> , starting at age 0, for the T-H lognormal model is determined by:
| |
| | |
| <br>
| |
| ::<math>R(T,V,U)=\mathop{}_{T}^{\infty }f(t,V,U)dt</math>
| |
| | |
| <br>
| |
| or:
| |
| <br>
| |
| ::<math>R(T,V,U)=\mathop{}_{{{T}^{^{\prime }}}}^{\infty }\frac{1}{{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{t-\ln (A)-\tfrac{\phi }{V}-\tfrac{b}{U}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}}dt</math>
| |
| | |
| <br>
| |
| There is no closed form solution for the lognormal reliability function. Solutions can be obtained via the use of standard normal tables. Since the application automatically solves for the reliability, we will not discuss manual solution methods.
| |
| <br>
| |
| <br>
| |
| ====Reliable Life====
| |
| <br>
| |
| For the T-H lognormal model, the reliable life, or the mission duration for a desired reliability goal, <math>{{t}_{R}},</math> is estimated by first solving the reliability equation with respect to time, as follows:
| |
| <br>
| |
| ::<math>T_{R}^{\prime }=\ln (A)+\frac{\phi }{V}+\frac{b}{U}+z\cdot {{\sigma }_{{{T}'}}}</math>
| |
| <br>
| |
| where:
| |
| <br>
| |
| ::<math>z={{\Phi }^{-1}}\left[ F\left( T_{R}^{\prime },V,U \right) \right]</math>
| |
| | |
| <br>
| |
| and:
| |
| <br>
| |
| ::<math>\Phi (z)=\frac{1}{\sqrt{2\pi }}\mathop{}_{-\infty }^{z({T}',V,U)}{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt</math>
| |
| | |
| <br>
| |
| Since <math>{T}'=\ln (T),</math> the reliable life, <math>{{t}_{R,}}</math> is given by:
| |
| | |
| <br>
| |
| ::<math>{{t}_{R}}={{e}^{T_{R}^{\prime }}}</math>
| |
| | |
| <br>
| |
| ====T-H Lognormal Failure Rate====
| |
| <br>
| |
| The lognormal failure rate is given by:
| |
| | |
| <br>
| |
| ::<math>\lambda (T,V,U)=\frac{f(T,V,U)}{R(T,V,U)}=\frac{\tfrac{1}{T\text{ }{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{T}'-\ln (A)-\tfrac{\phi }{V}-\tfrac{b}{U}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}}}{\mathop{}_{{{T}'}}^{\infty }\tfrac{1}{{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{T}'-\ln (A)-\tfrac{\phi }{V}-\tfrac{b}{U}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}}dt}</math>
| |
| | |
| <br>
| |
| ===Parameter Estimation===
| |
| <br>
| |
| ====Maximum Likelihood Estimation Method====
| |
| <br>
| |
| The complete T-H lognormal log-likelihood function is:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{1}{{{\sigma }_{{{T}'}}}{{T}_{i}}}{{\phi }_{pdf}}\left( \frac{\ln \left( {{T}_{i}} \right)-\ln (A)-\tfrac{\phi }{{{V}_{i}}}-\tfrac{b}{{{U}_{i}}}}{{{\sigma }_{{{T}'}}}} \right) \right] \\
| |
| & & \text{ }+\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\ln \left[ 1-\Phi \left( \frac{\ln \left( T_{i}^{\prime } \right)-\ln (A)-\tfrac{\phi }{{{V}_{i}}}-\tfrac{b}{{{U}_{i}}}}{{{\sigma }_{{{T}'}}}} \right) \right] \\
| |
| & & +\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime })]
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| where:
| |
| | |
| <br>
| |
| ::<math>z_{Li}^{\prime \prime }=\frac{\ln T_{Li}^{\prime \prime }-\ln A-\tfrac{\phi }{{{V}_{i}}}-\tfrac{b}{U_{i}^{\prime \prime }}}{\sigma _{T}^{\prime }}</math>
| |
| | |
| <br>
| |
| ::<math>z_{Ri}^{\prime \prime }=\frac{\ln T_{Ri}^{\prime \prime }-\ln A-\tfrac{\phi }{{{V}_{i}}}-\tfrac{b}{U_{i}^{\prime \prime }}}{\sigma _{T}^{\prime }}</math>
| |
| | |
| <br>
| |
| ::<math>{{\phi }_{pdf}}\left( x \right)=\frac{1}{\sqrt{2\pi }}\cdot {{e}^{-\tfrac{1}{2}{{\left( x \right)}^{2}}}}</math>
| |
| | |
| <br>
| |
| ::<math>\Phi (x)=\frac{1}{\sqrt{2\pi }}\mathop{}_{-\infty }^{x}{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt</math>
| |
| | |
| <br>
| |
| and:
| |
| <br>
| |
| • <math>{{F}_{e}}</math> is the number of groups of exact times-to-failure data points.
| |
| <br>
| |
| • <math>{{N}_{i}}</math> is the number of times-to-failure data points in the <math>{{i}^{th}}</math> time-to-failure data group.
| |
| <br>
| |
| • <math>{{\sigma }_{{{T}'}}}</math> is the standard deviation of the natural logarithm of the times-to-failure (unknown, the first of four parameters to be estimated).
| |
| <br>
| |
| • <math>A</math> is the first T-H parameter (unknown, the second of four parameters to be estimated).
| |
| <br>
| |
| • <math>\phi </math> is the second T-H parameter (unknown, the third of four parameters to be estimated).
| |
| <br>
| |
| • <math>b</math> is the third T-H parameter (unknown, the fourth of four parameters to be estimated).
| |
| <br>
| |
| • <math>{{V}_{i}}</math> is the stress level for the first stress type (i.e. temperature) of the <math>{{i}^{th}}</math> group.
| |
| <br>
| |
| • <math>{{U}_{i}}</math> is the stress level for the second stress type (i.e. relative humidity) of the <math>{{i}^{th}}</math> group.
| |
| <br>
| |
| • <math>{{T}_{i}}</math> is the exact failure time of the <math>{{i}^{th}}</math> group.
| |
| <br>
| |
| • <math>S</math> is the number of groups of suspension data points.
| |
| <br>
| |
| • <math>N_{i}^{\prime }</math> is the number of suspensions in the <math>{{i}^{th}}</math> group of suspension data points.
| |
| <br>
| |
| • <math>T_{i}^{\prime }</math> is the running time of the <math>{{i}^{th}}</math> suspension data group.
| |
| <br>
| |
| • <math>FI</math> is the number of interval data groups.
| |
| <br>
| |
| • <math>N_{i}^{\prime \prime }</math> is the number of intervals in the <math>{{i}^{th}}</math> group of data intervals.
| |
| <br>
| |
| • <math>T_{Li}^{\prime \prime }</math> is the beginning of the <math>{{i}^{th}}</math> interval.
| |
| • <math>T_{Ri}^{\prime \prime }</math> is the ending of the <math>{{i}^{th}}</math> interval.
| |
| <br>
| |
| •
| |
| <br>
| |
| The solution (parameter estimates) will be found by solving for <math>{{\widehat{\sigma }}_{{{T}'}}},</math> <math>\widehat{A},</math> <math>\widehat{\phi },</math> <math>\widehat{b}</math> so that <math>\tfrac{\partial \Lambda }{\partial {{\sigma }_{{{T}'}}}}=0,</math> <math>\tfrac{\partial \Lambda }{\partial A}=0,</math> <math>\tfrac{\partial \Lambda }{\partial \phi }=0</math> and <math>\tfrac{\partial \Lambda }{\partial b}=0</math> .
| |
| <br>
| |
| <br>
| |
| | |
| =Appendix 9A: T-H Confidence Bounds=
| |
| <br>
| |
| ==Approximate Confidence Bounds for the T-H Exponential==
| |
| <br>
| |
| ===Confidence Bounds on the Mean Life===
| |
| <br>
| |
| The mean life for the T-H exponential distribution is given by Eqn. (Temp-Hum) by setting <math>m=L(V)</math> . The upper <math>({{m}_{U}})</math> and lower <math>({{m}_{L}})</math> bounds on the mean life (ML estimate of the mean life) are estimated by:
| |
| <br>
| |
| ::<math>{{m}_{U}}=\widehat{m}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{m})}}{\widehat{m}}}}</math>
| |
| | |
| <br>
| |
| ::<math>{{m}_{L}}=\widehat{m}\cdot {{e}^{-\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{m})}}{\widehat{m}}}}</math>
| |
| <br>
| |
| where <math>{{K}_{\alpha }}</math> is defined by:
| |
| <br>
| |
| | |
| ::<math>\alpha =\frac{1}{\sqrt{2\pi }}\mathop{}_{{{K}_{\alpha }}}^{\infty }{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt=1-\Phi ({{K}_{\alpha }})</math>
| |
| | |
| <br>
| |
| If <math>\delta </math> is the confidence level, then <math>\alpha =\tfrac{1-\delta }{2}</math> for the two-sided bounds, and <math>\alpha =1-\delta </math> for the one-sided bounds. The variance of <math>\widehat{m}</math> is given by:
| |
| <br>
| |
| ::<math>\begin{align}
| |
| & Var(\widehat{m})= & {{\left( \frac{\partial m}{\partial A} \right)}^{2}}Var(\widehat{A})+{{\left( \frac{\partial m}{\partial \phi } \right)}^{2}}Var(\widehat{\phi }) \\
| |
| & & +{{\left( \frac{\partial m}{\partial b} \right)}^{2}}Var(\widehat{b}) \\
| |
| & & +2\left( \frac{\partial m}{\partial A} \right)\left( \frac{\partial m}{\partial \phi } \right)Cov(\widehat{A},\widehat{\phi }) \\
| |
| & & +2\left( \frac{\partial m}{\partial A} \right)\left( \frac{\partial m}{\partial b} \right)Cov(\widehat{A},\widehat{b}) \\
| |
| & & +2\left( \frac{\partial m}{\partial A} \right)\left( \frac{\partial m}{\partial \phi } \right)Cov(\widehat{\phi },\widehat{b})
| |
| \end{align}</math>
| |
| <br>
| |
| or:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & Var(\widehat{m})= & {{e}^{2\left( \tfrac{\widehat{\phi }}{V}+\tfrac{\widehat{b}}{U} \right)}}[Var(\widehat{A})+\frac{{{\widehat{A}}^{2}}}{{{V}^{2}}}Var(\widehat{\phi }) \\
| |
| & & +\frac{{{\widehat{A}}^{2}}}{{{U}^{2}}}Var(\widehat{b}) \\
| |
| & & +\frac{2\widehat{A}}{V}Cov(\widehat{A},\widehat{\phi })+\frac{2\widehat{A}}{U}Cov(\widehat{A},\widehat{b}) \\
| |
| & & +\frac{2{{\widehat{A}}^{2}}}{V\cdot U}Cov(\widehat{\phi },\widehat{b})]
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| The variances and covariance of <math>A</math> , <math>b</math> and <math>\phi </math> are estimated from the local Fisher matrix (evaluated at <math>\widehat{A},</math> <math>\widehat{b}</math> <math>,\widehat{\phi })</math> as follows:
| |
| | |
| <br>
| |
| ::<math>\left[ \begin{matrix}
| |
| Var(\widehat{A}) & Cov(\widehat{A},\widehat{\phi }) & Cov(\widehat{A},\widehat{b}) \\
| |
| Cov(\widehat{\phi },\widehat{A}) & Var(\widehat{\phi }) & Cov(\widehat{\phi },\widehat{b}) \\
| |
| Cov(\widehat{b},\widehat{A}) & Cov(\widehat{b},\widehat{\phi }) & Var(\widehat{b}) \\
| |
| \end{matrix} \right]=\left[ \begin{matrix}
| |
| -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{A}^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial A\partial \phi } & -\tfrac{{{\partial }^{2}}\Lambda }{\partial A\partial b} \\
| |
| -\tfrac{{{\partial }^{2}}\Lambda }{\partial \phi \partial A} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\phi }^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \phi \partial b} \\
| |
| -\tfrac{{{\partial }^{2}}\Lambda }{\partial b\partial A} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial b\partial \phi } & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{b}^{2}}} \\
| |
| \end{matrix} \right]_{}^{-1}</math>
| |
| | |
| | |
| ===Confidence Bounds on Reliability===
| |
| <br>
| |
| The bounds on reliability at a given time, <math>T</math> , are estimated by:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & {{R}_{U}}= & {{e}^{-\tfrac{T}{{{m}_{U}}}}} \\
| |
| & {{R}_{L}}= & {{e}^{-\tfrac{T}{{{m}_{L}}}}}
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| where <math>{{m}_{U}}</math> and <math>{{m}_{L}}</math> are estimated using Eqns. (THuUpper) and (THuLower).
| |
| <br>
| |
| ===Confidence Bounds on Time===
| |
| <br>
| |
| The bounds on time (ML estimate of time) for a given reliability are estimated by first solving the reliability function with respect to time or:
| |
| | |
| <br>
| |
| ::<math>\widehat{T}=-\widehat{m}\cdot \ln (R)</math>
| |
| | |
| <br>
| |
| The corresponding confidence bounds are estimated from:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & {{T}_{U}}= & -{{m}_{U}}\cdot \ln (R) \\
| |
| & {{T}_{L}}= & -{{m}_{L}}\cdot \ln (R)
| |
| \end{align}</math>
| |
| | |
| where <math>{{m}_{U}}</math> and <math>{{m}_{L}}</math> are estimated using Eqns. (THuUpper) and (THuLower).
| |
| <br>
| |
| <br>
| |
| ==Approximate Confidence Bounds for the T-H Weibull==
| |
| <br>
| |
| ===Bounds on the Parameters===
| |
| <br>
| |
| Using the same approach as previously discussed ( <math>\widehat{\beta }</math> and <math>\widehat{A}</math> positive parameters):
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & {{\beta }_{U}}= & \widehat{\beta }\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{\beta })}}{\widehat{\beta }}}} \\
| |
| & {{\beta }_{L}}= & \widehat{\beta }\cdot {{e}^{-\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{\beta })}}{\widehat{\beta }}}}
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & {{A}_{U}}= & \widehat{A}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{A})}}{\widehat{A}}}} \\
| |
| & {{A}_{L}}= & \widehat{A}\cdot {{e}^{-\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{A})}}{\widehat{A}}}}
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & {{b}_{U}}= & \widehat{b}+{{K}_{\alpha }}\sqrt{Var(\widehat{b})} \\
| |
| & {{b}_{L}}= & \widehat{b}-{{K}_{\alpha }}\sqrt{Var(\widehat{b})}
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| and:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & {{\phi }_{U}}= & \widehat{\phi }+{{K}_{\alpha }}\sqrt{Var(\widehat{\phi })} \\
| |
| & {{\phi }_{L}}= & \widehat{\phi }-{{K}_{\alpha }}\sqrt{Var(\widehat{\phi })}
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| The variances and covariances of <math>\beta ,</math> <math>A,</math> <math>b,</math> and <math>\phi </math> are estimated from the local Fisher matrix (evaluated at <math>\widehat{\beta },</math> <math>\widehat{A},</math> <math>\widehat{b},</math> <math>\widehat{\phi })</math> as follows:
| |
| | |
| <br>
| |
| ::<math>\left[ \begin{matrix}
| |
| Var(\widehat{\beta }) & Cov(\widehat{\beta },\widehat{A}) & Cov(\widehat{\beta },\widehat{b}) & Cov(\widehat{\beta },\widehat{\phi }) \\
| |
| Cov(\widehat{A},\widehat{\beta }) & Var(\widehat{A}) & Cov(\widehat{A},\widehat{b}) & Cov(\widehat{A},\widehat{\phi }) \\
| |
| Cov(\widehat{b},\widehat{\beta }) & Cov(\widehat{b},\widehat{A}) & Var(\widehat{b}) & Cov(\widehat{b},\widehat{\phi }) \\
| |
| Cov(\widehat{\phi },\widehat{\beta }) & Cov(\widehat{\phi },\widehat{A}) & Cov(\widehat{\phi },\widehat{b}) & Var(\widehat{\phi }) \\
| |
| \end{matrix} \right]={{\left[ F \right]}^{-1}}</math>
| |
| | |
| <br>
| |
| where:
| |
| <br>
| |
| ::<math>F=\left[ \begin{matrix}
| |
| -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\beta }^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \beta \partial A} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \beta \partial b} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \beta \partial \phi } \\
| |
| -\tfrac{{{\partial }^{2}}\Lambda }{\partial A\partial \beta } & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{A}^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial A\partial b} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial A\partial \phi } \\
| |
| -\tfrac{{{\partial }^{2}}\Lambda }{\partial b\partial \beta } & -\tfrac{{{\partial }^{2}}\Lambda }{\partial b\partial A} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{b}^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial b\partial \phi } \\
| |
| -\tfrac{{{\partial }^{2}}\Lambda }{\partial \phi \partial \beta } & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \phi \partial A} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \phi \partial b} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\phi }^{2}}} \\
| |
| \end{matrix} \right]</math>
| |
| | |
| <br>
| |
| ===Confidence Bounds on Reliability===
| |
| <br>
| |
| The reliability function (ML estimate) for the T-H Weibull model is given by:
| |
| | |
| <br>
| |
| ::<math>\widehat{R}(T,V,U)={{e}^{-{{\left( \tfrac{T}{\widehat{A}}{{e}^{-\left( \tfrac{\widehat{\phi }}{V}+\tfrac{\widehat{b}}{U} \right)}} \right)}^{\widehat{\beta }}}}}</math>
| |
| | |
| <br>
| |
| or:
| |
| | |
| <br>
| |
| ::<math>\widehat{R}(T,V,U)={{e}^{-{{e}^{\ln \left[ {{\left( \tfrac{T}{\widehat{A}}{{e}^{-\left( \tfrac{\widehat{\phi }}{V}+\tfrac{\widehat{b}}{U} \right)}} \right)}^{\widehat{\beta }}} \right]}}}}</math>
| |
| | |
| <br>
| |
| Setting:
| |
| | |
| <br>
| |
| ::<math>\widehat{u}=\ln \left[ {{\left( \frac{T}{\widehat{A}}{{e}^{-\left( \tfrac{\widehat{\phi }}{V}+\tfrac{\widehat{b}}{U} \right)}} \right)}^{\widehat{\beta }}} \right]</math>
| |
| | |
| <br>
| |
| or:
| |
| | |
| <br>
| |
| ::<math>\widehat{u}=\widehat{\beta }\left[ \ln (T)-\ln (\widehat{A})-\frac{\widehat{\phi }}{V}-\frac{\widehat{b}}{U} \right]</math>
| |
| | |
| <br>
| |
| The reliability function now becomes:
| |
| | |
| <br>
| |
| ::<math>\widehat{R}(T,V,U)={{e}^{-{{e}^{\widehat{u}}}}}</math>
| |
| | |
| <br>
| |
| The next step is to find the upper and lower bounds on <math>u</math> :
| |
| | |
| <br>
| |
| ::<math>{{\widehat{u}}_{U}}=\widehat{u}+{{K}_{\alpha }}\sqrt{Var(\widehat{u})}</math>
| |
| | |
| <br>
| |
| ::<math>{{\widehat{u}}_{L}}=\widehat{u}-{{K}_{\alpha }}\sqrt{Var(\widehat{u})}</math>
| |
| | |
| <br>
| |
| where:
| |
| <br>
| |
| <br>
| |
| ::<math>\begin{align}
| |
| & Var(\widehat{u})= & {{\left( \frac{\partial \widehat{u}}{\partial \beta } \right)}^{2}}Var(\widehat{\beta })+{{\left( \frac{\partial \widehat{u}}{\partial A} \right)}^{2}}Var(\widehat{A}) \\
| |
| & & +{{\left( \frac{\partial \widehat{u}}{\partial b} \right)}^{2}}Var(\widehat{b})+{{\left( \frac{\partial \widehat{u}}{\partial \phi } \right)}^{2}}Var(\widehat{\phi }) \\
| |
| & & +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial A} \right)Cov(\widehat{\beta },\widehat{A}) \\
| |
| & & +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial b} \right)Cov(\widehat{\beta },\widehat{b}) \\
| |
| & & +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial \phi } \right)Cov(\widehat{\beta },\widehat{\phi }) \\
| |
| & & +2\left( \frac{\partial \widehat{u}}{\partial A} \right)\left( \frac{\partial \widehat{u}}{\partial b} \right)Cov(\widehat{A},\widehat{b}) \\
| |
| & & +2\left( \frac{\partial \widehat{u}}{\partial A} \right)\left( \frac{\partial \widehat{u}}{\partial \phi } \right)Cov(\widehat{A},\widehat{\phi }) \\
| |
| & & +2\left( \frac{\partial \widehat{u}}{\partial b} \right)\left( \frac{\partial \widehat{u}}{\partial \phi } \right)Cov(\widehat{b},\widehat{\phi })
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| or:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & Var(\widehat{u})= & {{\left( \frac{\widehat{u}}{\widehat{\beta }} \right)}^{2}}Var(\widehat{\beta })+{{\left( \frac{\widehat{\beta }}{\widehat{A}} \right)}^{2}}Var(\widehat{A}) \\
| |
| & & +{{\left( \frac{\widehat{\beta }}{U} \right)}^{2}}Var(\widehat{b})+{{\left( \frac{\widehat{\beta }}{V} \right)}^{2}}Var(\widehat{\phi }) \\
| |
| & & -\frac{2\widehat{u}}{\widehat{A}}Cov(\widehat{\beta },\widehat{A})-\frac{2\widehat{u}}{U}Cov(\widehat{\beta },\widehat{b})-\frac{2\widehat{u}}{V}Cov(\widehat{\beta },\widehat{\phi }) \\
| |
| & & +\frac{2{{\widehat{\beta }}^{2}}}{\widehat{A}U}Cov(\widehat{A},\widehat{b})+\frac{2{{\widehat{\beta }}^{2}}}{\widehat{A}V}Cov(\widehat{A},\widehat{\phi }) \\
| |
| & & +\frac{2{{\widehat{\beta }}^{2}}}{UV}Cov(\widehat{\phi },\widehat{b})
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| The upper and lower bounds on reliability are:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & {{R}_{U}}= & {{e}^{-{{e}^{\left( {{u}_{L}} \right)}}}} \\
| |
| & {{R}_{L}}= & {{e}^{-{{e}^{\left( {{u}_{U}} \right)}}}}
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| where <math>{{u}_{U}}</math> and <math>{{u}_{L}}</math> are estimated using Eqns. (THUupper) and (THUlower).
| |
| <br>
| |
| <br>
| |
| ===Confidence Bounds on Time===
| |
| <br>
| |
| The bounds on time (ML estimate of time) for a given reliability are estimated by first solving the reliability function with respect to time as follows:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & \ln (R)= & -{{\left( \frac{\widehat{T}}{\widehat{A}}{{e}^{-\left( \tfrac{\widehat{\phi }}{V}+\tfrac{\widehat{b}}{U} \right)}} \right)}^{\widehat{\beta }}} \\
| |
| & \ln (-\ln (R))= & \widehat{\beta }\left( \ln \widehat{T}-\ln \widehat{A}-\frac{\widehat{\phi }}{V}-\frac{\widehat{b}}{U} \right)
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| or:
| |
| | |
| <br>
| |
| ::<math>\widehat{u}=\frac{1}{\widehat{\beta }}\ln (-\ln (R))+\ln \widehat{A}+\frac{\widehat{\phi }}{V}+\frac{\widehat{b}}{U}</math>
| |
| | |
| <br>
| |
| where <math>\widehat{u}=\ln \widehat{T}.</math>
| |
| | |
| <br>
| |
| The upper and lower bounds on <math>u</math> are estimated from:
| |
| | |
| <br>
| |
| ::<math>{{u}_{U}}=\widehat{u}+{{K}_{\alpha }}\sqrt{Var(\widehat{u})}</math>
| |
| | |
| <br>
| |
| ::<math>{{u}_{L}}=\widehat{u}-{{K}_{\alpha }}\sqrt{Var(\widehat{u})}</math>
| |
| | |
| <br>
| |
| where:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & Var(\widehat{u})= & {{\left( \frac{\partial \widehat{u}}{\partial \beta } \right)}^{2}}Var(\widehat{\beta })+{{\left( \frac{\partial \widehat{u}}{\partial A} \right)}^{2}}Var(\widehat{A}) \\
| |
| & & +{{\left( \frac{\partial \widehat{u}}{\partial b} \right)}^{2}}Var(\widehat{b})+{{\left( \frac{\partial \widehat{u}}{\partial \phi } \right)}^{2}}Var(\widehat{\phi }) \\
| |
| & & +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial A} \right)Cov(\widehat{\beta },\widehat{A}) \\
| |
| & & +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial b} \right)Cov(\widehat{\beta },\widehat{b}) \\
| |
| & & +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial \phi } \right)Cov(\widehat{\beta },\widehat{\phi }) \\
| |
| & & +2\left( \frac{\partial \widehat{u}}{\partial A} \right)\left( \frac{\partial \widehat{u}}{\partial b} \right)Cov(\widehat{A},\widehat{b}) \\
| |
| & & +2\left( \frac{\partial \widehat{u}}{\partial A} \right)\left( \frac{\partial \widehat{u}}{\partial \phi } \right)Cov(\widehat{A},\widehat{\phi }) \\
| |
| & & +2\left( \frac{\partial \widehat{u}}{\partial b} \right)\left( \frac{\partial \widehat{u}}{\partial \phi } \right)Cov(\widehat{b},\widehat{\phi })
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| or:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & Var(\widehat{u})= & \frac{1}{{{\widehat{\beta }}^{4}}}{{\left[ \ln (-\ln (R)) \right]}^{2}}Var(\widehat{\beta })+\frac{1}{{{\widehat{A}}^{2}}}Var(\widehat{A}) \\
| |
| & & +\frac{1}{{{U}^{2}}}Var(\widehat{b})+\frac{1}{{{V}^{2}}}Var(\widehat{\phi }) \\
| |
| & & +\frac{2\ln (-\ln (R))}{{{\widehat{\beta }}^{2}}\widehat{A}}Cov(\widehat{\beta },\widehat{A}) \\
| |
| & & -\frac{2\ln (-\ln (R))}{{{\widehat{\beta }}^{2}}U}Cov(\widehat{\beta },\widehat{b}) \\
| |
| & & -\frac{2\ln (-\ln (R))}{{{\widehat{\beta }}^{2}}V}Cov(\widehat{\beta },\widehat{\phi }) \\
| |
| & & +\frac{2}{\widehat{A}U}Cov(\widehat{A},\widehat{b}) \\
| |
| & & +\frac{2}{\widehat{A}V}Cov(\widehat{A},\widehat{\phi }) \\
| |
| & & +\frac{2}{VU}Cov(\widehat{b},\widehat{\phi })
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| The upper and lower bounds on time are then found by:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & {{T}_{U}}= & {{e}^{{{u}_{U}}}} \\
| |
| & {{T}_{L}}= & {{e}^{{{u}_{L}}}}
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| where <math>{{u}_{U}}</math> and <math>{{u}_{L}}</math> are estimated using Eqns. (THUupper) and (THUlower).
| |
| | |
| <br>
| |
| ==Approximate Confidence Bounds for the T-H Lognormal==
| |
| <br>
| |
| ===Bounds on the Parameters===
| |
| <br>
| |
| Since the standard deviation, <math>{{\widehat{\sigma }}_{{{T}'}}}</math> , and <math>\widehat{A}</math> are positive parameters, <math>\ln ({{\widehat{\sigma }}_{{{T}'}}})</math> and <math>\ln (\widehat{A})</math> are treated as normally distributed and the bounds are estimated from:
| |
| <br>
| |
| ::<math>\begin{align}
| |
| & {{\sigma }_{U}}= & {{\widehat{\sigma }}_{{{T}'}}}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var({{\widehat{\sigma }}_{{{T}'}}})}}{{{\widehat{\sigma }}_{{{T}'}}}}}}\text{ (Upper bound)} \\
| |
| & {{\sigma }_{L}}= & \frac{{{\widehat{\sigma }}_{{{T}'}}}}{{{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var({{\widehat{\sigma }}_{{{T}'}}})}}{{{\widehat{\sigma }}_{{{T}'}}}}}}}\text{ (Lower bound)}
| |
| \end{align}</math>
| |
| <br>
| |
| and:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & {{A}_{U}}= & \widehat{A}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{A})}}{\widehat{A}}}}\text{ (Upper bound)} \\
| |
| & {{A}_{L}}= & \frac{\widehat{A}}{{{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{A})}}{\widehat{A}}}}}\text{ (Lower bound)}
| |
| \end{align}</math>
| |
| <br>
| |
| The lower and upper bounds on <math>\phi </math> and <math>b</math> are estimated from:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & {{\phi }_{U}}= & \widehat{\phi }+{{K}_{\alpha }}\sqrt{Var(\widehat{\phi })}\text{ (Upper bound)} \\
| |
| & {{\phi }_{L}}= & \widehat{\phi }-{{K}_{\alpha }}\sqrt{Var(\widehat{\phi })}\text{ (Lower bound)}
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| and:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & {{b}_{U}}= & \widehat{b}+{{K}_{\alpha }}\sqrt{Var(\widehat{b})}\text{ (Upper bound)} \\
| |
| & {{b}_{L}}= & \widehat{b}-{{K}_{\alpha }}\sqrt{Var(\widehat{b})}\text{ (Lower bound)}
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| ::The variances and covariances of <math>A</math> , <math>\phi ,</math> <math>b,</math> and <math>{{\sigma }_{{{T}'}}}</math> are estimated from the local Fisher matrix (evaluated at <math>\widehat{A}</math> , <math>\widehat{\phi },</math> <math>\widehat{b}</math> , <math>{{\widehat{\sigma }}_{{{T}'}}}),</math> as follows:
| |
| | |
| <br>
| |
| ::<math>\left( \begin{matrix}
| |
| Var\left( {{\widehat{\sigma }}_{{{T}'}}} \right) & Cov\left( \widehat{A},{{\widehat{\sigma }}_{{{T}'}}} \right) & Cov\left( \widehat{\phi },{{\widehat{\sigma }}_{{{T}'}}} \right) & Cov\left( \widehat{b},{{\widehat{\sigma }}_{{{T}'}}} \right) \\
| |
| Cov\left( {{\widehat{\sigma }}_{{{T}'}}},\widehat{A} \right) & Var\left( \widehat{A} \right) & Cov\left( \widehat{A},\widehat{\phi } \right) & Cov\left( \widehat{A},\widehat{b} \right) \\
| |
| Cov\left( {{\widehat{\sigma }}_{{{T}'}}},\widehat{\phi } \right) & Cov\left( \widehat{\phi },\widehat{A} \right) & Var\left( \widehat{\phi } \right) & Cov\left( \widehat{\phi },\widehat{b} \right) \\
| |
| Cov\left( \widehat{b},{{\widehat{\sigma }}_{{{T}'}}} \right) & Cov\left( \widehat{b},\widehat{A} \right) & Cov\left( \widehat{b},\widehat{\phi } \right) & Var\left( \widehat{b} \right) \\
| |
| \end{matrix} \right)={{F}^{-1}}</math>
| |
| | |
| <br>
| |
| where:
| |
| | |
| <br>
| |
| ::<math>{{F}^{-1}}={{\left( \begin{matrix}
| |
| -\tfrac{{{\partial }^{2}}\Lambda }{\partial \sigma _{{{T}'}}^{2}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\sigma }_{{{T}'}}}\partial A} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\sigma }_{{{T}'}}}\partial \phi } & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\sigma }_{{{T}'}}}\partial b} \\
| |
| -\tfrac{{{\partial }^{2}}\Lambda }{\partial A\partial {{\sigma }_{{{T}'}}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{A}^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial A\partial \phi } & -\tfrac{{{\partial }^{2}}\Lambda }{\partial A\partial b} \\
| |
| -\tfrac{{{\partial }^{2}}\Lambda }{\partial \phi \partial {{\sigma }_{{{T}'}}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \phi \partial A} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\phi }^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \phi \partial b} \\
| |
| -\tfrac{{{\partial }^{2}}\Lambda }{\partial b\partial {{\sigma }_{{{T}'}}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial b\partial A} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial b\partial \phi } & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{b}^{2}}} \\
| |
| \end{matrix} \right)}^{-1}}</math>
| |
| | |
| <br>
| |
| ===Bounds on Reliability===
| |
| <br>
| |
| The reliability of the lognormal distribution is given by:
| |
| | |
| <br>
| |
| ::<math>R({T}',V,U;A,\phi ,b,{{\sigma }_{{{T}'}}})=\mathop{}_{{{T}'}}^{\infty }\frac{1}{{{\widehat{\sigma }}_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{t-\ln (\widehat{A})-\tfrac{\widehat{\phi }}{V}-\tfrac{\widehat{b}}{U}}{{{\widehat{\sigma }}_{{{T}'}}}} \right)}^{2}}}}dt</math>
| |
| | |
| <br>
| |
| Let <math>\widehat{z}(t,V,U;A,\phi ,b,{{\sigma }_{T}})=\tfrac{t-\ln (\widehat{A})-\tfrac{\widehat{\phi }}{V}-\tfrac{\widehat{b}}{U}}{{{\widehat{\sigma }}_{{{T}'}}}},</math> then <math>\tfrac{d\widehat{z}}{dt}=\tfrac{1}{{{\widehat{\sigma }}_{{{T}'}}}}.</math>
| |
| For <math>t={T}'</math> , <math>\widehat{z}=\tfrac{{T}'-\ln (\widehat{A})-\tfrac{\widehat{\phi }}{V}-\tfrac{\widehat{b}}{U}}{{{\widehat{\sigma }}_{{{T}'}}}}</math> , and for <math>t=\infty ,</math> <math>\widehat{z}=\infty .</math> The above equation then becomes:
| |
| | |
| <br>
| |
| ::<math>R(\widehat{z})=\mathop{}_{\widehat{z}({T}',V,U)}^{\infty }\frac{1}{\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz</math>
| |
| | |
| <br>
| |
| The bounds on <math>z</math> are estimated from:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & {{z}_{U}}= & \widehat{z}+{{K}_{\alpha }}\sqrt{Var(\widehat{z})} \\
| |
| & {{z}_{L}}= & \widehat{z}-{{K}_{\alpha }}\sqrt{Var(\widehat{z})}
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| where:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & Var(\widehat{z})= & \left( \frac{\partial \widehat{z}}{\partial A} \right)_{\widehat{A}}^{2}Var(\widehat{A})+\left( \frac{\partial \widehat{z}}{\partial \phi } \right)_{\widehat{\phi }}^{2}Var(\widehat{\phi }) \\
| |
| & & +\left( \frac{\partial \widehat{z}}{\partial b} \right)_{\widehat{b}}^{2}Var(\widehat{b})+\left( \frac{\partial \widehat{z}}{\partial {{\sigma }_{{{T}'}}}} \right)_{{{\widehat{\sigma }}_{{{T}'}}}}^{2}Var({{\widehat{\sigma }}_{{{T}'}}}) \\
| |
| & & +2{{\left( \frac{\partial \widehat{z}}{\partial A} \right)}_{\widehat{A}}}{{\left( \frac{\partial \widehat{z}}{\partial \phi } \right)}_{\widehat{\phi }}}Cov\left( \widehat{A},\widehat{\phi } \right) \\
| |
| & & +2{{\left( \frac{\partial \widehat{z}}{\partial A} \right)}_{\widehat{A}}}{{\left( \frac{\partial \widehat{z}}{\partial b} \right)}_{\widehat{b}}}Cov\left( \widehat{A},\widehat{b} \right) \\
| |
| & & +2{{\left( \frac{\partial \widehat{z}}{\partial \phi } \right)}_{\widehat{\phi }}}{{\left( \frac{\partial \widehat{z}}{\partial b} \right)}_{\widehat{b}}}Cov\left( \widehat{\phi },\widehat{b} \right) \\
| |
| & & +2{{\left( \frac{\partial \widehat{z}}{\partial A} \right)}_{\widehat{A}}}{{\left( \frac{\partial \widehat{z}}{\partial {{\sigma }_{{{T}'}}}} \right)}_{{{\widehat{\sigma }}_{{{T}'}}}}}Cov\left( \widehat{A},{{\widehat{\sigma }}_{{{T}'}}} \right) \\
| |
| & & +2{{\left( \frac{\partial \widehat{z}}{\partial \phi } \right)}_{\widehat{\phi }}}{{\left( \frac{\partial \widehat{z}}{\partial {{\sigma }_{{{T}'}}}} \right)}_{{{\widehat{\sigma }}_{{{T}'}}}}}Cov\left( \widehat{\phi },{{\widehat{\sigma }}_{{{T}'}}} \right) \\
| |
| & & +2{{\left( \frac{\partial \widehat{z}}{\partial b} \right)}_{\widehat{b}}}{{\left( \frac{\partial \widehat{z}}{\partial {{\sigma }_{{{T}'}}}} \right)}_{{{\widehat{\sigma }}_{{{T}'}}}}}Cov\left( \widehat{b},{{\widehat{\sigma }}_{{{T}'}}} \right)
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| or:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & Var(\widehat{z})= & \frac{1}{\widehat{\sigma }_{{{T}'}}^{2}}[\frac{1}{{{A}^{2}}}Var(\widehat{A})+\frac{1}{{{V}^{2}}}Var(\widehat{\phi })+\frac{1}{{{U}^{2}}}Var(\widehat{b})+{{\widehat{z}}^{2}}Var({{\widehat{\sigma }}_{{{T}'}}}) \\
| |
| & & +\frac{2}{A\cdot V}Cov\left( \widehat{A},\widehat{\phi } \right)+\frac{2}{A\cdot U}Cov\left( \widehat{A},\widehat{b} \right) \\
| |
| & & +\frac{2}{V\cdot U}Cov\left( \widehat{\phi },\widehat{b} \right)+\frac{2\widehat{z}}{A}Cov\left( \widehat{A},{{\widehat{\sigma }}_{{{T}'}}} \right) \\
| |
| & & +\frac{2\widehat{z}}{V}Cov\left( \widehat{\phi },{{\widehat{\sigma }}_{{{T}'}}} \right)+\frac{2\widehat{z}}{U}Cov\left( \widehat{b},{{\widehat{\sigma }}_{{{T}'}}} \right)]
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| The upper and lower bounds on reliability are:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & {{R}_{U}}= & \mathop{}_{{{z}_{L}}}^{\infty }\frac{1}{\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz\text{ (Upper bound)} \\
| |
| & {{R}_{L}}= & \mathop{}_{{{z}_{U}}}^{\infty }\frac{1}{\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz\text{ (Lower bound)}
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| ===Confidence Bounds on Time===
| |
| <br>
| |
| The bounds around time, for a given lognormal percentile (unreliability), are estimated by first solving the reliability equation with respect to time, as follows:
| |
| | |
| <br>
| |
| ::<math>{T}'(V,U;\widehat{A},\widehat{\phi },\widehat{b},{{\widehat{\sigma }}_{{{T}'}}})=\ln (\widehat{A})+\frac{\widehat{\phi }}{V}+\frac{\widehat{b}}{U}+z\cdot {{\widehat{\sigma }}_{{{T}'}}}</math>
| |
| <br>
| |
| where:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & {T}'(V,U;\widehat{A},\widehat{\phi },\widehat{b},{{\widehat{\sigma }}_{{{T}'}}})= & \ln (T) \\
| |
| & z= & {{\Phi }^{-1}}\left[ F({T}') \right]
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| and:
| |
| | |
| <br>
| |
| ::<math>\Phi (z)=\frac{1}{\sqrt{2\pi }}\mathop{}_{-\infty }^{z({T}')}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz</math>
| |
| | |
| <br>
| |
| The next step is to calculate the variance of <math>{T}'(V,U;\widehat{A},\widehat{\phi },\widehat{b},{{\widehat{\sigma }}_{{{T}'}}})</math> as follows:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & Var({T}')= & {{\left( \frac{\partial {T}'}{\partial A} \right)}^{2}}Var(\widehat{A})+{{\left( \frac{\partial {T}'}{\partial \phi } \right)}^{2}}Var(\widehat{\phi }) \\
| |
| & & +{{\left( \frac{\partial {T}'}{\partial b} \right)}^{2}}Var(\widehat{b})+{{\left( \frac{\partial {T}'}{\partial {{\sigma }_{{{T}'}}}} \right)}^{2}}Var({{\widehat{\sigma }}_{{{T}'}}}) \\
| |
| & & +2\left( \frac{\partial {T}'}{\partial A} \right)\left( \frac{\partial {T}'}{\partial \phi } \right)Cov\left( \widehat{A},\widehat{\phi } \right) \\
| |
| & & +2\left( \frac{\partial {T}'}{\partial A} \right)\left( \frac{\partial {T}'}{\partial b} \right)Cov\left( \widehat{A},\widehat{b} \right) \\
| |
| & & +2\left( \frac{\partial {T}'}{\partial \phi } \right)\left( \frac{\partial {T}'}{\partial b} \right)Cov\left( \widehat{\phi },\widehat{b} \right) \\
| |
| & & +2\left( \frac{\partial {T}'}{\partial A} \right)\left( \frac{\partial {T}'}{\partial {{\sigma }_{{{T}'}}}} \right)Cov\left( \widehat{A},{{\widehat{\sigma }}_{{{T}'}}} \right) \\
| |
| & & +2\left( \frac{\partial {T}'}{\partial \phi } \right)\left( \frac{\partial {T}'}{\partial {{\sigma }_{{{T}'}}}} \right)Cov\left( \widehat{\phi },{{\widehat{\sigma }}_{{{T}'}}} \right) \\
| |
| & & +2\left( \frac{\partial {T}'}{\partial b} \right)\left( \frac{\partial {T}'}{\partial {{\sigma }_{{{T}'}}}} \right)Cov\left( \widehat{b},{{\widehat{\sigma }}_{{{T}'}}} \right)
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| or:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & Var({T}')= & \frac{1}{{{A}^{2}}}Var(\widehat{A})+\frac{1}{{{V}^{2}}}Var(\widehat{\phi }) \\
| |
| & & +\frac{1}{{{U}^{2}}}Var(\widehat{b})+{{\widehat{z}}^{2}}Var({{\widehat{\sigma }}_{{{T}'}}}) \\
| |
| & & +\frac{2}{A\cdot V}Cov\left( \widehat{A},\widehat{\phi } \right)+\frac{2}{A\cdot U}Cov\left( \widehat{A},\widehat{b} \right) \\
| |
| & & +\frac{2}{V\cdot U}Cov\left( \widehat{\phi },\widehat{b} \right)+\frac{2\widehat{z}}{A}Cov\left( \widehat{A},{{\widehat{\sigma }}_{{{T}'}}} \right) \\
| |
| & & +\frac{2\widehat{z}}{V}Cov\left( \widehat{\phi },{{\widehat{\sigma }}_{{{T}'}}} \right)+\frac{2\widehat{z}}{U}Cov\left( \widehat{b},{{\widehat{\sigma }}_{{{T}'}}} \right)
| |
| \end{align}</math>
| |
| <br>
| |
| <br>
| |
| The upper and lower bounds are then found by:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & T_{U}^{\prime }= & \ln {{T}_{U}}={T}'+{{K}_{\alpha }}\sqrt{Var({T}')} \\
| |
| & T_{L}^{\prime }= & \ln {{T}_{L}}={T}'-{{K}_{\alpha }}\sqrt{Var({T}')}
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| Solving for <math>{{T}_{U}}</math> and <math>{{T}_{L}}</math> yields:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & {{T}_{U}}= & {{e}^{T_{U}^{\prime }}}\text{ (Upper bound)} \\
| |
| & {{T}_{L}}= & {{e}^{T_{L}^{\prime }}}\text{ (Lower bound)}
| |
| \end{align}</math>
| |
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images, more targeted search and the latest content available as a PDF. As of September 2023, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest reference at help.reliasoft.com/reference/accelerated_life_testing_data_analysis
|
Chapter 9: Multivariable Relationships: General Log-Linear and Proportional Hazards
|
|

| Chapter 9
|
| Multivariable Relationships: General Log-Linear and Proportional Hazards
|
Available Software:
ALTA
More Resources:
ALTA Examples
|
So far in this reference the life-stress relationships presented have been either single stress relationships or two stress relationships. In most practical applications, however, life is a function of more than one or two variables (stress types). In addition, there are many applications where the life of a product as a function of stress and of some engineering variable other than stress is sought. In this chapter, the general log-linear relationship and the proportional hazards model are presented for the analysis of such cases where more than two accelerated stresses (or variables) need to be considered.
General Log-Linear Relationship
When a test involves multiple accelerating stresses or requires the inclusion of an engineering variable, a general multivariable relationship is needed. Such a relationship is the general log-linear relationship, which describes a life characteristic as a function of a vector of [math]\displaystyle{ n\,\! }[/math] stresses, or [math]\displaystyle{ \underline{X}=({{X}_{1}},{{X}_{2}}...{{X}_{n}}).\,\! }[/math] ALTA includes this relationship and allows up to eight stresses. Mathematically the relationship is given by:
- [math]\displaystyle{ L(\underline{X})={{e}^{{{\alpha }_{0}}+\underset{j=1}{\overset{n}{\mathop{\sum }}}\,{{\alpha }_{j}}{{X}_{j}}}}\,\! }[/math]
where:
- [math]\displaystyle{ {{\alpha }_{0}}\,\! }[/math] and [math]\displaystyle{ {{\alpha }_{j}}\,\! }[/math] are model parameters.
- [math]\displaystyle{ X\,\! }[/math] is a vector of [math]\displaystyle{ n\,\! }[/math] stresses.
This relationship can be further modified through the use of transformations and can be reduced to the relationships discussed previously, if so desired. As an example, consider a single stress application of this relationship and an inverse transformation on [math]\displaystyle{ X,\,\! }[/math] such that [math]\displaystyle{ V=1/X\,\! }[/math] or:
- [math]\displaystyle{ \begin{align}
& L(V)= & {{e}^{{{\alpha }_{0}}+\tfrac{{{\alpha }_{1}}}{V}}} =\ & {{e}^{{{\alpha }_{0}}}}{{e}^{\tfrac{{{\alpha }_{1}}}{V}}}
\end{align}\,\! }[/math]
It can be easily seen that the generalized log-linear relationship with a single stress and an inverse transformation has been reduced to the Arrhenius relationship, where:
- [math]\displaystyle{ \begin{align}
& C= & {{e}^{{{\alpha }_{0}}}} \\
& B= & {{\alpha }_{1}}
\end{align}\,\! }[/math]
or:
- [math]\displaystyle{ L(V)=C{{e}^{\tfrac{B}{V}}}\,\! }[/math]
Similarly, when one chooses to apply a logarithmic transformation on [math]\displaystyle{ X\,\! }[/math] such that [math]\displaystyle{ X=\ln (V)\,\! }[/math], the relationship would reduce to the Inverse Power Law relationship. Furthermore, if more than one stress is present, one could choose to apply a different transformation to each stress to create combination relationships similar to the Temperature-Humidity and the Temperature-Non Thermal. ALTA has three built-in transformation options, namely:
| None |
[math]\displaystyle{ X=V\,\! }[/math] |
Exponential LSR
|
| Reciprocal |
[math]\displaystyle{ X=1/V\,\! }[/math] |
Arrhenius LSR
|
| Logarithmic |
[math]\displaystyle{ X=\ln (V)\,\! }[/math] |
Power LSR
|
The power of the relationship and this formulation becomes evident once one realizes that 6,561 unique life-stress relationships are possible (when allowing a maximum of eight stresses). When combined with the life distributions available in ALTA, almost 20,000 models can be created.
Using the GLL Model
Like the previous relationships, the general log-linear relationship can be combined with any of the available life distributions by expressing a life characteristic from that distribution with the GLL relationship. A brief overview of the GLL-distribution models available in ALTA is presented next.
GLL Exponential
The GLL-exponential model can be derived by setting [math]\displaystyle{ m=L(\underline{X})\,\! }[/math] in the exponential pdf, yielding the following GLL-exponential pdf:
[math]\displaystyle{ f(t,\underline{X})={{e}^{-\left( {{\alpha }_{0}}+\underset{j=1}{\overset{n}{\mathop{\sum }}}\,{{\alpha }_{j}}{{X}_{j}} \right)}}{{e}^{-\left( {{\alpha }_{0}}+\underset{j=1}{\overset{n}{\mathop{\sum }}}\,{{\alpha }_{j}}{{X}_{j}} \right)\cdot t}}\,\! }[/math]
The total number of unknowns to solve for in this model is [math]\displaystyle{ n+1\,\! }[/math] (i.e., [math]\displaystyle{ {{a}_{0}},{{a}_{1}},...{{a}_{n}}).\,\! }[/math]
GLL Weibull
The GLL-Weibull model can be derived by setting [math]\displaystyle{ \eta =L(\underline{X})\,\! }[/math] in Weibull pdf, yielding the following GLL-Weibull pdf:
[math]\displaystyle{ f(t,\underline{X})=\beta \cdot {{t}^{\beta -1}}{{e}^{-\beta \left( {{\alpha }_{0}}+\underset{j=1}{\overset{n}{\mathop{\sum }}}\,{{\alpha }_{j}}{{X}_{j}} \right)}}{{e}^{-{{t}^{\beta }}{{e}^{-\beta \left( {{\alpha }_{0}}+\underset{j=1}{\overset{n}{\mathop{\sum }}}\,{{\alpha }_{j}}{{X}_{j}} \right)}}}}\,\! }[/math]
The total number of unknowns to solve for in this model is [math]\displaystyle{ n+2\,\! }[/math] (i.e., [math]\displaystyle{ \beta ,{{a}_{0}},{{a}_{1}},...{{a}_{n}}).\,\! }[/math]
GLL Lognormal
The GLL-lognormal model can be derived by setting [math]\displaystyle{ \breve{T}=L(\underline{X})\,\! }[/math]
in the lognormal pdf, yielding the following GLL-lognormal pdf:
[math]\displaystyle{ f(t,\underline{X})=\frac{1}{t\text{ }{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{T}'-{{\alpha }_{0}}-\underset{j=1}{\overset{n}{\mathop{\sum }}}\,{{\alpha }_{j}}{{X}_{j}}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}}\,\! }[/math]
The total number of unknowns to solve for in this model is [math]\displaystyle{ n+2\,\! }[/math] (i.e., [math]\displaystyle{ {{\sigma }_{{{T}'}}},{{a}_{0}},{{a}_{1}},...{{a}_{n}}).\,\! }[/math]
GLL Likelihood Function
The maximum likelihood estimation method can be used to determine the parameters for the GLL relationship and the selected life distribution. For each distribution, the likelihood function can be derived, and the parameters of model (the distribution parameters and the GLL parameters) can be obtained by maximizing the log-likelihood function. For example, the log-likelihood function for the Weibull distribution is given by:
- [math]\displaystyle{ \begin{align}
\ln (L) = \Lambda = & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \beta \cdot T_{i}^{\beta -1}{{e}^{-T_{i}^{\beta }\cdot {{e}^{-\beta \left( {{\alpha }_{0}}+\mathop{\sum}_{j=1}^{n}{{a}_{j}}{{x}_{i,j}} \right)}}}}{{e}^{-\beta \left( {{\alpha }_{0}}+\mathop{\sum}_{j=1}^{n}{{a}_{j}}{{x}_{i,j}} \right)}} \right] \\
& -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }{{\left( T_{i}^{\prime } \right)}^{\beta }}{{e}^{-\beta \left( {{\alpha }_{0}}+\mathop{\sum}_{j=1}^{n}{{a}_{j}}{{x}_{i,j}} \right)}}+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }]
\end{align}\,\! }[/math]
where:
- [math]\displaystyle{ \begin{align}
& R_{Li}^{\prime \prime }= & {{e}^{-{{\left( T_{Li}^{\prime \prime }{{e}^{{{\alpha }_{0}}+\underset{j=1}{\mathop{\overset{n}{\mathop{\mathop{}_{}^{}}}\,}}\,{{\alpha }_{j}}{{x}_{j}}}} \right)}^{\beta }}}} \\
& R_{Ri}^{\prime \prime }= & {{e}^{-{{\left( T_{Ri}^{\prime \prime }{{e}^{{{\alpha }_{0}}+\underset{j=1}{\mathop{\overset{n}{\mathop{\mathop{}_{}^{}}}\,}}\,{{\alpha }_{j}}{{x}_{j}}}} \right)}^{\beta }}}}
\end{align}\,\! }[/math]
and:
- [math]\displaystyle{ {{F}_{e}}\,\! }[/math] is the number of groups of exact times-to-failure data points.
- [math]\displaystyle{ {{N}_{i}}\,\! }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] time-to-failure data group.
- [math]\displaystyle{ \lambda \,\! }[/math] is the failure rate parameter (unknown).
- [math]\displaystyle{ {{T}_{i}}\,\! }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group.
- [math]\displaystyle{ S\,\! }[/math] is the number of groups of suspension data points.
- [math]\displaystyle{ N_{i}^{\prime }\,\! }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of suspension data points.
- [math]\displaystyle{ T_{i}^{\prime }\,\! }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] suspension data group.
- [math]\displaystyle{ FI\,\! }[/math] is the number of interval data groups.
- [math]\displaystyle{ N_{i}^{\prime \prime }\,\! }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of data intervals.
- [math]\displaystyle{ T_{Li}^{\prime \prime }\,\! }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] interval.
- [math]\displaystyle{ T_{Ri}^{\prime \prime }\,\! }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] interval.
GLL Example
Consider the data summarized in the following tables. These data illustrate a typical three-stress type accelerated test.
Stress Profile Summary
Failure Data
The data in the second table are analyzed assuming a Weibull distribution, an Arrhenius life-stress relationship for temperature and an inverse power life-stress relationship for voltage. No transformation is performed on the operation type. The operation type variable is treated as an indicator variable that takes a discrete value of 0 for an on/off operation and 1 for a continuous operation. The following figure shows the stress types and their transformations in ALTA.
The GLL relationship then becomes:
- [math]\displaystyle{ \eta ={{e}^{{{\alpha }_{0}}+{{\alpha }_{1}}\tfrac{1}{{{V}_{1}}}+{{\alpha }_{2}}\ln ({{V}_{2}})+{{\alpha }_{3}}{{V}_{3}}}}\,\! }[/math]
The resulting relationship after performing these transformations is:
- [math]\displaystyle{ \begin{align}
& \eta = & {{e}^{{{\alpha }_{0}}}}{{e}^{{{\alpha }_{1}}\tfrac{1}{{{V}_{1}}}}}{{e}^{{{\alpha }_{2}}\ln ({{V}_{2}})}}{{e}^{{{\alpha }_{3}}{{V}_{3}}}} =\ & {{e}^{{{\alpha }_{0}}}}{{e}^{{{\alpha }_{1}}\tfrac{1}{{{V}_{1}}}}}V_{2}^{{{\alpha }_{2}}}{{e}^{{{\alpha }_{3}}{{V}_{3}}}}
\end{align}\,\! }[/math]
Therefore, the parameter [math]\displaystyle{ B\,\! }[/math] of the Arrhenius relationship is equal to the log-linear coefficient [math]\displaystyle{ {{\alpha }_{1}}\,\! }[/math], and the parameter [math]\displaystyle{ n\,\! }[/math] of the inverse power relationship is equal to ([math]\displaystyle{ -{{\alpha}_{2}}\,\! }[/math]). Therefore [math]\displaystyle{ \eta \,\! }[/math] can also be written as:
- [math]\displaystyle{ \eta ={{e}^{{{\alpha }_{0}}}}{{e}^{\tfrac{B}{{{V}_{1}}}}}V_{2}^{n}{{e}^{{{\alpha }_{3}}{{V}_{3}}}}\,\! }[/math]
The activation energy of the Arrhenius relationship can be calculated by multiplying B with Boltzmann's constant.
The best fit values for the parameters in this case are:
- [math]\displaystyle{ \begin{align}
\beta = & 3.7483;\text{ }{{\alpha }_{0}} = -6.0220;\text{ }{{\alpha }_{1}} = 5776.9341; \\
{{\alpha }_{2}} = & -1.4340;\text{ }{{\alpha }_{3}} = 0.6242.
\end{align}\,\! }[/math]
Once the parameters are estimated, further analysis on the data can be performed. First, using ALTA, a Weibull probability plot of the data can be obtained, as shown next.
Several types of information about the model as well as the data can be obtained from a probability plot. For example, the choice of an underlying distribution and the assumption of a common slope (shape parameter) can be examined. In this example, the linearity of the data supports the use of the Weibull distribution. In addition, the data appear parallel on this plot, therefore reinforcing the assumption of a common beta. Further statistical analysis can and should be performed for these purposes as well.
The Life vs. Stress plot is a very common plot for the analysis of accelerated data. Life vs. Stress plots can be very useful in assessing the effect of each stress on a product's failure. In this case, since the life is a function of three stresses, three different plots can be created. Such plots are created by holding two of the stresses constant at the desired use level, and varying the remaining one. The use stress levels for this example are 328K for temperature and 10V for voltage. For the operation type, a decision has to be made by the engineers as to whether they implement an on/off or continuous operation. The next two figures display the effects of temperature and voltage on the life of the product.
The effects of the two different operation types on life can be observed in the next figure. It can be seen that the on/off cycling has a greater effect on the life of the product in terms of accelerating failure than the continuous operation. In other words, a higher reliability can be achieved by running the product continuously.
Proportional Hazards Model
Introduced by D. R. Cox, the Proportional Hazards (PH) model was developed in order to estimate the effects of different covariates influencing the times-to-failure of a system.
The model has been widely used in the biomedical field, as discussed in Leemis [22], and recently there has been an increasing interest in its application in reliability engineering. In its original form, the model is non-parametric, (i.e., no assumptions are made about the nature or shape of the underlying failure distribution). In this reference, the original non-parametric formulation as well as a parametric form of the model will be considered utilizing a Weibull life distribution. In ALTA, the proportional hazards model is included in its parametric form and can be used to analyze data with up to eight variables. The GLL-Weibull and GLL-exponential models are actually special cases of the proportional hazards model. However, when using the proportional hazards in ALTA, no transformation on the covariates (or stresses) can be performed.
Non-Parametric Model Formulation
According to the PH model, the failure rate of a system is affected not only by its operation time, but also by the covariates under which it operates. For example, a unit may have been tested under a combination of different accelerated stresses such as humidity, temperature, voltage, etc. It is clear then that such factors affect the failure rate of a unit.
The instantaneous failure rate (or hazard rate) of a unit is given by:
- [math]\displaystyle{ \lambda (t)=\frac{f(t)}{R(t)}\,\! }[/math]
where:
- [math]\displaystyle{ f(t)\,\! }[/math] is the probability density function.
- [math]\displaystyle{ R(t)\,\! }[/math] is the reliability function.
Note that for the case of the failure rate of a unit being dependent not only on time but also on other covariates, the above equation must be modified in order to be a function of time and of the covariates.
The proportional hazards model assumes that the failure rate (hazard rate) of a unit is the product of:
- an arbitrary and unspecified baseline failure rate, [math]\displaystyle{ {{\lambda }_{0}}(t),\,\! }[/math] which is a function of time only.
- a positive function [math]\displaystyle{ g(x,\underline{A})\,\! }[/math], independent of time, which incorporates the effects of a number of covariates such as humidity, temperature, pressure, voltage, etc.
The failure rate of a unit is then given by:
- [math]\displaystyle{ \lambda (t,\underline{X})={{\lambda }_{0}}(t)\cdot g(\underline{X},\underline{A})\,\! }[/math]
where:
- [math]\displaystyle{ \underline{X}\,\! }[/math] is a row vector consisting of the covariates:
- [math]\displaystyle{ \underline{X}=({{x}_{1}},{{x}_{2}},...,{{x}_{m}})\,\! }[/math]
- [math]\displaystyle{ \underline{A}\,\! }[/math] is a column vector consisting of the unknown parameters (also called regression parameters) of the model:
- [math]\displaystyle{ \underline{A}={{({{a}_{1}},{{a}_{2}},...{{a}_{m}})}^{T}}\,\! }[/math]
- where:
- [math]\displaystyle{ \quad \quad m\,\! }[/math] = number of stress related variates (time-independent).
It can be assumed that the form of [math]\displaystyle{ g(\underline{X},\underline{A})\,\! }[/math] is known and [math]\displaystyle{ {{\lambda }_{0}}(t)\,\! }[/math] is unspecified. Different forms of [math]\displaystyle{ g(\underline{X},\underline{A})\,\! }[/math] can be used.
However, the exponential form is mostly used due to its simplicity and is given by:
- [math]\displaystyle{ g(\underline{X},\underline{A})={{e}^{{{\underline{A}}^{T}}{{\underline{X}}^{T}}}}={{e}^{\mathop{\sum}_{j=1}^{m}{{a}_{j}}{{x}_{j}}}}\,\! }[/math]
The failure rate can then be written as:
- [math]\displaystyle{ \lambda (t,\underline{X})={{\lambda }_{0}}(t)\cdot {{e}^{\mathop{\sum}_{j=1}^{m}{{a}_{j}}{{x}_{j}}}}\,\! }[/math]
Parametric Model Formulation
A parametric form of the proportional hazards model can be obtained by assuming an underlying distribution. In ALTA, the Weibull and exponential distributions are available. In this section we will consider the Weibull distribution to formulate the parametric proportional hazards model. In other words, it is assumed that the baseline failure rate is parametric and given by the Weibull distribution. In this case, the baseline failure rate is given by:
- [math]\displaystyle{ {{\lambda }_{0}}(t)=\frac{\beta }{\eta }{{\left( \frac{t}{\eta } \right)}^{\beta -1}}\,\! }[/math]
The PH failure rate then becomes:
- [math]\displaystyle{ \lambda (t,\underline{X})=\frac{\beta }{\eta }{{\left( \frac{t}{\eta } \right)}^{\beta -1}}\cdot {{e}^{\mathop{\sum}_{j=1}^{m}{{a}_{j}}{{x}_{j}}}}\,\! }[/math]
It is often more convenient to define an additional covariate, [math]\displaystyle{ {{x}_{0}} = 1\,\! }[/math], in order to allow the Weibull scale parameter raised to the beta (shape parameter) to be included in the vector of regression coefficients. The PH failure rate can then be written as:
- [math]\displaystyle{ \lambda (t,\underline{X})=\beta \cdot {{t}^{\beta -1}}\cdot {{e}^{\mathop{\sum}_{j=0}^{m}{{a}_{j}}{{x}_{j}}}}\,\! }[/math]
The PH reliability function is given by:
- [math]\displaystyle{ \begin{align}
R(t,\underline{X})=\ {{e}^{-\int_{0}^{t}\lambda (u)du}} =\ {{e}^{-\int_{0}^{t}\lambda (u,\underline{X})du}} =\ {{e}^{-{{t}^{\beta }}\cdot {{e}^{\mathop{\sum}_{j=0}^{m}{{a}_{j}}{{x}_{j}}}}}}
\end{align}\,\! }[/math]
The pdf can be obtained by taking the partial derivative of the reliability function with respect to time. The PH pdf is:
- [math]\displaystyle{ \begin{align}
f(t,\underline{X})= & \lambda (t,\underline{X})\cdot R(t,\underline{X}) =\ \beta \cdot {{t}^{\beta -1}}{{e}^{\left[ \mathop{\sum}_{j=0}^{m}{{a}_{j}}{{x}_{j}}-{{t}^{\beta }}\cdot {{e}^{\mathop{\sum}_{j=0}^{m}{{a}_{j}}{{x}_{j}}}} \right]}}
\end{align}\,\! }[/math]
The total number of unknowns to solve for in this model is [math]\displaystyle{ m+2\,\! }[/math] (i.e., [math]\displaystyle{ \beta ,{{a}_{0}},{{a}_{1}},...{{a}_{m}}\,\! }[/math]).
The maximum likelihood estimation method can be used to determine these parameters. The log-likelihood function for this case is given by:
- [math]\displaystyle{ \begin{align}
\ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left( \beta \cdot T_{i}^{\beta -1}{{e}^{-T_{i}^{\beta }\cdot {{e}^{\mathop{\sum}_{j=0}^{m}{{a}_{j}}{{x}_{i,j}}}}}}{{e}^{\mathop{\sum}_{j=0}^{m}{{a}_{j}}{{x}_{i,j}}}} \right) -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }{{\left( T_{i}^{\prime } \right)}^{\beta }}{{e}^{\mathop{\sum}_{j=0}^{m}{{a}_{j}}{{x}_{i,j}}}}+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }]
\end{align}\,\! }[/math]
where:
- [math]\displaystyle{ \begin{align}
& R_{Li}^{\prime \prime }= & {{e}^{-T_{Li}^{\prime \prime \beta }{{e}^{\underset{j=0}{\mathop{\overset{n}{\mathop{\mathop{\sum}_{}^{}}}\,}}\,{{\alpha }_{j}}{{x}_{j}}}}}} \\
& R_{Ri}^{\prime \prime }= & {{e}^{-T_{Ri}^{\prime \prime \beta }{{e}^{\underset{j=0}{\mathop{\overset{n}{\mathop{\mathop{\sum}_{}^{}}}\,}}\,{{\alpha }_{j}}{{x}_{j}}}}}}
\end{align}\,\! }[/math]
Solving for the parameters that maximize the log-likelihood function will yield the parameters for the PH-Weibull model. Note that for [math]\displaystyle{ \beta =1 \,\! }[/math], the log-likelihood function becomes the log-likelihood function for the PH-exponential model, which is similar to the original form of the proportional hazards model proposed by Cox and Oakes [39].
Note that the likelihood function of the GLL model is very similar to the likelihood function for the proportional hazards-Weibull model. In particular, the shape parameter of the Weibull distribution can be included in the regression coefficients as follows:
- [math]\displaystyle{ {{a}_{i,PH}}=-\beta \cdot {{a}_{i,GLL}}\,\! }[/math]
where:
- [math]\displaystyle{ {{a}_{i,PH}}\,\! }[/math] are the parameters of the PH model.
- [math]\displaystyle{ {{a}_{i,GLL}}\,\! }[/math] are the parameters of the general log-linear model.
In this case, the likelihood functions are identical. Therefore, if no transformation on the covariates is performed, the parameter values that maximize the likelihood function of the GLL model also maximize the likelihood function for the proportional hazards-Weibull (PHW) model. Note that for [math]\displaystyle{ \beta = 1\,\! }[/math] (exponential life distribution), the two likelihood functions are identical, and [math]\displaystyle{ {{a}_{i,PH}}=-{{a}_{i,GLL}}.\,\! }[/math]
Indicator Variables
Another advantage of the multivariable relationships included in ALTA is that they allow for simultaneous analysis of continuous and categorical variables. Categorical variables are variables that take on discrete values such as the lot designation for products from different manufacturing lots. In this example, lot is a categorical variable, and it can be expressed in terms of indicator variables. Indicator variables only take a value of 1 or 0. For example, consider a sample of test units. A number of these units were obtained from Lot 1, others from Lot 2, and the rest from Lot 3. These three lots can be represented with the use of indicator variables, as follows:
- Define two indicator variables, [math]\displaystyle{ {{X}_{1}}\,\! }[/math] and [math]\displaystyle{ {{X}_{2}}.\,\! }[/math]
- For the units from Lot 1, [math]\displaystyle{ {{X}_{1}}=1,\,\! }[/math] and [math]\displaystyle{ {{X}_{2}}=0.\,\! }[/math]
- For the units from Lot 2, [math]\displaystyle{ {{X}_{1}}=0,\,\! }[/math] and [math]\displaystyle{ {{X}_{2}}=1.\,\! }[/math]
- For the units from Lot 3, [math]\displaystyle{ {{X}_{1}}=0,\,\! }[/math] and [math]\displaystyle{ {{X}_{2}}=0.\,\! }[/math]
Assume that an accelerated test was performed with these units, and temperature was the accelerated stress. In this case, the GLL relationship can be used to analyze the data. From the GLL relationship we get:
- [math]\displaystyle{ L(\underline{X})={{e}^{{{\alpha }_{0}}+{{\alpha }_{1}}{{X}_{1}}+{{\alpha }_{2}}{{X}_{2}}+{{\alpha }_{3}}{{X}_{3}}}}\,\! }[/math]
where:
- [math]\displaystyle{ {{X}_{1}}\,\! }[/math] and [math]\displaystyle{ {{X}_{2}}\,\! }[/math] are the indicator variables, as defined above.
- [math]\displaystyle{ {{X}_{3}}=\tfrac{1}{T},\,\! }[/math] where [math]\displaystyle{ T\,\! }[/math] is the temperature.
The data can now be entered in ALTA and, with the assumption of an underlying life distribution and using MLE, the parameters of this model can be obtained.