Non-Parametric Life Data Analysis: Difference between revisions

From ReliaWiki
Jump to navigation Jump to search
 
(33 intermediate revisions by 6 users not shown)
Line 1: Line 1:
{{template:LDABOOK|22|Non-Parametric Life Data Analysis}}
{{template:LDABOOK|17|Non-Parametric Life Data Analysis}}
Non-parametric analysis allows the user to analyze data without assuming an underlying distribution. This can have certain advantages as well as disadvantages. The ability to analyze data without assuming an underlying life distribution avoids the potentially large errors brought about by making incorrect assumptions about the distribution. On the other hand, the confidence bounds associated with non-parametric analysis are usually much wider than those calculated via parametric analysis, and predictions outside the range of the observations are not possible. Some practitioners recommend that any set of life data should first be subjected to a non-parametric analysis before moving on to the assumption of an underlying distribution.


==Nonparametric Analysis==


Nonparametric analysis allows the user to analyze data without assuming an underlying distribution. This can have certain advantages as well as disadvantages. The ability to analyze data without assuming an underlying life distribution avoids the potentially large errors brought about by making incorrect assumptions about the distribution. On the other hand, the confidence bounds associated with nonparametric analysis are usually much wider than those calculated via parametric analysis, and predictions outside the range of the observations are not possible. Some practitioners recommend that any set of life data should first be subjected to a nonparametric analysis before moving on to the assumption of an underlying distribution.
There are several methods for conducting a non-parametric analysis. In Weibull++, this includes the Kaplan-Meier, actuarial-simple and actuarial-standard methods. A method for attaching confidence bounds to the results of these non-parametric analysis techniques can also be developed. The basis of non-parametric life data analysis is the empirical ''cdf'' function, which is given by:  
There are several methods for conducting a nonparametric analysis, including the Kaplan-Meier, simple actuarial, and standard actuarial methods. A method for attaching confidence bounds to the results of these nonparametric analysis techniques can also be developed. The basis of nonparametric life data analysis is the empirical <math>cdf</math>  function, which is given by:




::<math>\widehat{F}(t)=\frac{observations\le t}{n}</math>
::<math>\widehat{F}(t)=\frac{observations\le t}{n}\,\!</math>




Note that this is similar to the Bernard's approximation of the median ranks, as discussed in Chapter 3. The following nonparametric analysis methods are essentially variations of this concept.
Note that this is similar to the Benard's approximation of the median ranks, as discussed in the [[Parameter Estimation]]&nbsp;chapter. The following non-parametric analysis methods are essentially variations of this concept.


===Kaplan-Meier Estimator===
== Kaplan-Meier Estimator ==
 
The Kaplan-Meier estimator, also known as the product limit estimator, can be used to calculate values for non-parametric reliability for data sets with multiple failures and suspensions. The equation of the estimator is given by:  
The Kaplan-Meier estimator, also known as the product limit estimator, can be used to calculate values for nonparametric reliability for data sets with multiple failures and suspensions. The equation of the estimator is given by:
 
 
::<math>\widehat{R}({{t}_{i}})=\underset{j=1}{\overset{i}{\mathop \prod }}\,\frac{{{n}_{j}}-{{r}_{j}}}{{{n}_{j}}},\text{ }i=1,...,m</math>


::<math>\widehat{R}({{t}_{i}})=\underset{j=1}{\overset{i}{\mathop \prod }}\,\frac{{{n}_{j}}-{{r}_{j}}}{{{n}_{j}}},\text{ }i=1,...,m\,\!</math>


where:  
where:  


::<math>\begin{align}
::<math>\begin{align}
   & m= & \text{the total number of data points} \\  
   & m= \text{the total number of data points} \\  
  & n= & \text{the total number of units}   
  & n= \text{the total number of units}   
\end{align}</math>
\end{align}\,\!</math>


The variable <math>{{n}_{i}}\,\!</math> is defined by:


The variable  <math>{{n}_{i}}</math>  is defined by:
::<math>{{n}_{i}}=n-\underset{j=0}{\overset{i-1}{\mathop \sum }}\,{{s}_{j}}-\underset{j=0}{\overset{i-1}{\mathop \sum }}\,{{r}_{j,}}\text{ }i=1,...,m\,\!</math>
 
 
::<math>{{n}_{i}}=n-\underset{j=0}{\overset{i-1}{\mathop \sum }}\,{{s}_{j}}-\underset{j=0}{\overset{i-1}{\mathop \sum }}\,{{r}_{j,}}\text{ }i=1,...,m</math>
 
 
where:


where:


::<math>\begin{align}
::<math>\begin{align}
   & {{r}_{j}}= & \text{the number of failures in the }{{j}^{th}}\text{ data group} \\  
   & {{r}_{j}}= \text{the number of failures in the }{{j}^{th}}\text{ data group} \\  
  & {{s}_{j}}= & \text{the number of suspensions in the }{{j}^{th}}\text{ data group}   
  & {{s}_{j}}= \text{the number of suspensions in the }{{j}^{th}}\text{ data group}   
\end{align}</math>
\end{align}\,\!</math>
 
 
Note that the reliability estimate is only calculated for times at which one or more failures occurred. For the sake of calculating the value of  <math>{{n}_{j}}</math>  at time values that have failures and suspensions, it is assumed that the suspensions occur slightly after the failures, so that the suspended units are considered to be operating and included in the count of  <math>{{n}_{j}}</math> .


====Example 9====
Note that the reliability estimate is only calculated for times at which one or more failures occurred. For the sake of calculating the value of <math>{{n}_{j}}\,\!</math> at time values that have failures and suspensions, it is assumed that the suspensions occur slightly after the failures, so that the suspended units are considered to be operating and included in the count of <math>{{n}_{j}}\,\!</math>.  
A group of 20 units are put on a life test with the following results.


===Kaplan-Meier Example===


A group of 20 units are put on a life test with the following results.
<center><math>\begin{matrix}
<center><math>\begin{matrix}
   Number & State & State  \\
   Number & State & State  \\
Line 70: Line 60:
   1 & S & 39  \\
   1 & S & 39  \\
   1 & S & 41  \\
   1 & S & 41  \\
\end{matrix}</math></center>
\end{matrix}\,\!</math></center>
 
Use the Kaplan-Meier estimator to determine the reliability estimates for each failure time.


Use the Kaplan-Meier estimator to determine the reliability estimates for each failure time.
'''Solution'''


=====Solution to Example 9=====
Using the data and the reliability equation of the Kaplan-Meier estimator, the following table can be constructed:  
Using the data and Eqn. (kapmeier), the following table can be constructed:  


<center><math>\begin{matrix}
<center><math>\begin{matrix}
   State & Number of & Number of & Available  & {} & {}  \\
   State & Number of & Number of & Available  & {} & {}  \\
   End Time & Failures, {{r}_{i}} & Suspensions, {{s}_{i}} & Units, {{n}_{i}} & \tfrac{{{n}_{i}}-{{r}_{i}}}{{{n}_{i}}} & \mathop{}_{}^{}\tfrac{{{n}_{i}}-{{r}_{i}}}{{{n}_{i}}}  \\
   End Time & Failures, {{r}_{i}} & Suspensions, {{s}_{i}} & Units, {{n}_{i}} & \tfrac{{{n}_{i}}-{{r}_{i}}}{{{n}_{i}}} & \mathop{}_{}^{}\prod\tfrac{{{n}_{i}}-{{r}_{i}}}{{{n}_{i}}}  \\
   9 & 3 & 1 & 20 & 0.850 & 0.850  \\
   9 & 3 & 1 & 20 & 0.850 & 0.850  \\
   11 & 1 & 0 & 16 & 0.938 & 0.797  \\
   11 & 1 & 0 & 16 & 0.938 & 0.797  \\
Line 96: Line 87:
   39 & 0 & 1 & 2 & 1.000 & 0.404  \\
   39 & 0 & 1 & 2 & 1.000 & 0.404  \\
   41 & 0 & 1 & 1 & 1.000 & 0.404  \\
   41 & 0 & 1 & 1 & 1.000 & 0.404  \\
\end{matrix}</math></center>
\end{matrix}\,\!</math></center>
 
 
 
 
As can be determined from the preceding table, the reliability estimates for the failure times are:


As can be determined from the preceding table, the reliability estimates for the failure times are:


<center><math>\begin{matrix}
<center><math>\begin{matrix}
Line 113: Line 100:
   28 & 50.5%  \\
   28 & 50.5%  \\
   30 & 40.4%  \\
   30 & 40.4%  \\
\end{matrix}</math></center>
\end{matrix}\,\!</math></center>
 
===Simple Actuarial Method===
The simple actuarial method is an easy-to-use form of nonparametric data analysis that can be used for multiply censored data that are arranged in intervals. This method is based on calculating the number of failures in a time interval,  <math>{{r}_{j}},</math>  versus the number of operating units in that time period,  <math>{{n}_{j}}</math> . The equation for the reliability estimator for the standard actuarial method is given by:


== Actuarial-Simple Method  ==
The&nbsp;actuarial-simple method is an easy-to-use form of non-parametric data analysis that can be used for multiple censored data that are arranged in intervals. This method is based on calculating the number of failures in a time interval, <math>{{r}_{j}}\,\!</math> versus the number of operating units in that time period, <math>{{n}_{j}}\,\!</math>. The equation for the reliability estimator for the standard actuarial method is given by:


::<math>\widehat{R}({{t}_{i}})=\underset{j=1}{\overset{i}{\mathop \prod }}\,\left( 1-\frac{{{r}_{j}}}{{{n}_{j}}} \right),\text{ }i=1,...,m</math>
::<math>\widehat{R}({{t}_{i}})=\underset{j=1}{\overset{i}{\mathop \prod }}\,\left( 1-\frac{{{r}_{j}}}{{{n}_{j}}} \right),\text{ }i=1,...,m\,\!</math>


where:  
where:  


::<math>\begin{align}
::<math>\begin{align}
   & m= & \text{the total number of intervals} \\  
   & m= \text{the total number of intervals} \\  
  & n= & \text{the total number of units}   
  & n= \text{the total number of units}   
\end{align}</math>
\end{align}\,\!</math>
 
 
The variable  <math>{{n}_{i}}</math>  is defined by:


::<math>{{n}_{i}}=n-\underset{j=0}{\overset{i-1}{\mathop \sum }}\,{{s}_{j}}-\underset{j=0}{\overset{i-1}{\mathop \sum }}\,{{r}_{j,}}\text{ }i=1,...,m</math>
The variable <math>{{n}_{i}}\,\!</math> is defined by:


::<math>{{n}_{i}}=n-\underset{j=0}{\overset{i-1}{\mathop \sum }}\,{{s}_{j}}-\underset{j=0}{\overset{i-1}{\mathop \sum }}\,{{r}_{j,}}\text{ }i=1,...,m\,\!</math>


where:  
where:  


::<math>\begin{align}
::<math>\begin{align}
   & {{r}_{j}}= & \text{the number of failures in interval }j \\  
   & {{r}_{j}}= \text{the number of failures in interval }j \\  
  & {{s}_{j}}= & \text{the number of suspensions in interval }j   
  & {{s}_{j}}= \text{the number of suspensions in interval }j   
\end{align}</math>
\end{align}\,\!</math>
 
 
 
====Example 10====
A group of 55 units are put on a life test during which the units are evaluated every 50 hours, with the following results:


===Actuarial-Simple Example===


A group of 55 units are put on a life test during which the units are evaluated every 50 hours. The results are:
<center><math>\begin{matrix}
<center><math>\begin{matrix}
   Start & End & Number of & Number of  \\
   Start & End & Number of & Number of  \\
Line 163: Line 144:
   550 & 600 & 1 & 0  \\
   550 & 600 & 1 & 0  \\
   600 & 650 & 2 & 1  \\
   600 & 650 & 2 & 1  \\
\end{matrix}</math></center>
\end{matrix}\,\!</math></center>
 
 


=====Solution to Example 10=====
'''Solution'''
The reliability estimates for the simple actuarial method can be obtained by expanding the data table to include terms used in calculation of the reliability estimates for Eqn. (simpact):


The reliability estimates&nbsp;can be obtained by expanding the data table to include the calculations used&nbsp;in the&nbsp;actuarial-simple method:
<center><math>\begin{matrix}
<center><math>\begin{matrix}
   Start & End & Number of & Number of & Available & {} & {}  \\
   Start & End & Number of & Number of & Available & {} & {}  \\
   Time & Time & Failures, {{r}_{i}} & Suspensions, {{s}_{i}} & Units, {{n}_{i}} & 1-\tfrac{{{r}_{j}}}{{{n}_{j}}} & \mathop{}_{}^{}1-\tfrac{{{r}_{j}}}{{{n}_{j}}}  \\
   Time & Time & Failures, {{r}_{i}} & Suspensions, {{s}_{i}} & Units, {{n}_{i}} & 1-\tfrac{{{r}_{j}}}{{{n}_{j}}} & \prod\mathop{}_{}^{}1-\tfrac{{{r}_{j}}}{{{n}_{j}}}  \\
   0 & 50 & 2 & 4 & 55 & 0.964 & 0.964  \\
   0 & 50 & 2 & 4 & 55 & 0.964 & 0.964  \\
   50 & 100 & 0 & 5 & 49 & 1.000 & 0.964  \\
   50 & 100 & 0 & 5 & 49 & 1.000 & 0.964  \\
Line 186: Line 165:
   550 & 600 & 1 & 0 & 4 & 0.750 & 0.245  \\
   550 & 600 & 1 & 0 & 4 & 0.750 & 0.245  \\
   600 & 650 & 2 & 1 & 3 & 0.333 & 0.082  \\
   600 & 650 & 2 & 1 & 3 & 0.333 & 0.082  \\
\end{matrix}</math></center>
\end{matrix}\,\!</math></center>


As can be determined from the preceding table, the reliability estimates for the failure times are:  
As can be determined from the preceding table, the reliability estimates for the failure times are:  
Line 205: Line 184:
   600 & 24.5%  \\
   600 & 24.5%  \\
   650 & 8.2%  \\
   650 & 8.2%  \\
\end{matrix}</math></center>
\end{matrix}\,\!</math></center>
 
===Standard Actuarial Method===
The standard actuarial model is a variation of the simple actuarial model that involves adjusting the value for the number of operating units in an interval. The Kaplan-Meier and simple actuarial methods assume that the suspensions in a time period or interval occur at the end of that interval, after the failures have occurred. The standard actuarial model assumes that the suspensions occur in the middle of the interval, which has the effect of reducing the number of available units in the interval by half of the suspensions in that interval or:


== Actuarial-Standard Method  ==
The&nbsp;actuarial-standard model is a variation of the&nbsp;actuarial-simple model. In the&nbsp;actuarial-simple method,&nbsp;the suspensions in a time period or interval are assumed to occur at the end of that interval, after the failures have occurred. The&nbsp;actuarial-standard model assumes that the suspensions occur in the middle of the interval, which has the effect of reducing the number of available units in the interval by half of the suspensions in that interval or:


::<math>n_{i}^{\prime }={{n}_{i}}-\frac{{{s}_{i}}}{2}</math>
::<math>n_{i}^{\prime }={{n}_{i}}-\frac{{{s}_{i}}}{2}\,\!</math>


With this adjustment, the calculations are carried out just as they were for the simple actuarial model in Eqn. (simpact) or:
With this adjustment, the calculations are carried out just as they were for the&nbsp;actuarial-simple model or:  


::<math>\widehat{R}({{t}_{i}})=\underset{j=1}{\overset{i}{\mathop \prod }}\,\left( 1-\frac{{{r}_{j}}}{n_{j}^{\prime }} \right),\text{ }i=1,...,m\,\!</math>


::<math>\widehat{R}({{t}_{i}})=\underset{j=1}{\overset{i}{\mathop \prod }}\,\left( 1-\frac{{{r}_{j}}}{n_{j}^{\prime }} \right),\text{ }i=1,...,m</math>
===Actuarial-Standard Example===


Use the data set from the Actuarial-Simple example and analyze it using the actuarial-standard method.


====Example 11====
'''Solution'''
Find reliability estimates for the data in Example 10 using the standard actuarial method.
=====Solution to Example 11=====
The solution to this example is similar to that of Example 10, with the exception of the inclusion of the  <math>n_{i}^{\prime }</math>  term, which is used in Eqn. (standact). Applying this equation to the data, we can generate the following table:


The solution to this example is similar to that in the Actuarial-Simple example, with the exception of the inclusion of the <math>n_{i}^{\prime }\,\!</math> term, which is used in the equation for the actuarial-standard method. Applying this equation to the data, we can generate the following table:
<center><math>\begin{matrix}
<center><math>\begin{matrix}
   Start & End & Number of & Number of & Adjusted & {} & {}  \\
   Start & End & Number of & Number of & Adjusted & {} & {}  \\
   Time & Time & Failures, {{r}_{i}} & Suspensions, {{s}_{i}} & Units, n_{i}^{\prime } & 1-\tfrac{{{r}_{j}}}{n_{j}^{\prime }} & \mathop{}_{}^{}1-\tfrac{{{r}_{j}}}{n_{j}^{\prime }}  \\
   Time & Time & Failures, {{r}_{i}} & Suspensions, {{s}_{i}} & Units, n_{i}^{\prime } & 1-\tfrac{{{r}_{j}}}{n_{j}^{\prime }} & \prod\mathop{}_{}^{}1-\tfrac{{{r}_{j}}}{n_{j}^{\prime }}  \\
   0 & 50 & 2 & 4 & 53 & 0.962 & 0.962  \\
   0 & 50 & 2 & 4 & 53 & 0.962 & 0.962  \\
   50 & 100 & 0 & 5 & 46.5 & 1.000 & 0.962  \\
   50 & 100 & 0 & 5 & 46.5 & 1.000 & 0.962  \\
Line 240: Line 218:
   550 & 600 & 1 & 0 & 4 & 0.750 & 0.223  \\
   550 & 600 & 1 & 0 & 4 & 0.750 & 0.223  \\
   600 & 650 & 2 & 1 & 2.5 & 0.200 & 0.045  \\
   600 & 650 & 2 & 1 & 2.5 & 0.200 & 0.045  \\
\end{matrix}</math></center>
\end{matrix}\,\!</math></center>


As can be determined from the preceding table, the reliability estimates for the failure times are:


As can be determined from the preceding table, the reliability estimates for the failure times are:
<center><math>\begin{matrix}
  Failure Period & Reliability  \\
  End Time & Estimate  \\
  50 & 96.2%  \\
  150 & 91.8%  \\
  200 & 84.4%  \\
  250 & 79.1%  \\
  300 & 76.2%  \\
  350 & 70.2%  \\
  400 & 60.4%  \\
  450 & 48.4%  \\
  500 & 43.0%  \\
  550 & 29.8%  \\
  600 & 22.3%  \\
  650 & 4.5%  \\
\end{matrix}\,\!</math></center>


===Nonparametric Confidence Bounds===
== Non-Parametric Confidence Bounds ==
Confidence bounds for nonparametric reliability estimates can be calculated using a method similar to that of parametric confidence bounds. The difficulty in dealing with nonparametric data lies in the estimation of the variance. To estimate the variance for nonparametric data, Weibull++ uses Greenwood's formula [27]:  
Confidence bounds for non-parametric reliability estimates can be calculated using a method similar to that of parametric confidence bounds. The difficulty in dealing with nonparametric data lies in the estimation of the variance. To estimate the variance for non-parametric data, Weibull++ uses Greenwood's formula [[Appendix:_Life_Data_Analysis_References|[27]]]:  


::<math>\widehat{Var}(\widehat{R}({{t}_{i}}))={{\left[ \widehat{R}({{t}_{i}}) \right]}^{2}}\cdot \underset{j=1}{\overset{i}{\mathop \sum }}\,\frac{\tfrac{{{r}_{j}}}{{{n}_{j}}}}{{{n}_{j}}\cdot \left( 1-\tfrac{{{r}_{j}}}{{{n}_{j}}} \right)}</math>
::<math>\widehat{Var}(\hat{R}({{t}_{i}}))={{\left[ \hat{R}({{t}_{i}}) \right]}^{2}}\cdot \underset{j=1}{\overset{i}{\mathop \sum }}\,\frac{\tfrac{{{r}_{j}}}{{{n}_{j}}}}{{{n}_{j}}\cdot \left( 1-\tfrac{{{r}_{j}}}{{{n}_{j}}} \right)}\,\!</math>


where:  
where:  


::<math>\begin{align}
::<math>\begin{align}
   & m= & \text{ the total number of intervals} \\  
   & m= \text{ the total number of intervals} \\  
  & n= & \text{ the total number of units}   
  & n= \text{ the total number of units}   
\end{align}</math>
\end{align}\,\!</math>


The variable <math>{{n}_{i}}</math> is defined by:  
The variable <math>{{n}_{i}}\,\!</math> is defined by:  


::<math>{{n}_{i}}=n-\underset{j=0}{\overset{i-1}{\mathop \sum }}\,{{s}_{j}}-\underset{j=0}{\overset{i-1}{\mathop \sum }}\,{{r}_{j,}}\text{ }i=1,...,m</math>
::<math>{{n}_{i}}=n-\underset{j=0}{\overset{i-1}{\mathop \sum }}\,{{s}_{j}}-\underset{j=0}{\overset{i-1}{\mathop \sum }}\,{{r}_{j,}}\text{ }i=1,...,m\,\!</math>


where:  
where:  


::<math>\begin{align}
::<math>\begin{align}
   & {{r}_{j}}= & \text{the number of failures in interval }j \\  
   & {{r}_{j}}= \text{the number of failures in interval }j \\  
  & {{s}_{j}}= & \text{the number of suspensions in interval }j   
  & {{s}_{j}}= \text{the number of suspensions in interval }j   
\end{align}</math>
\end{align}\,\!</math>


Once the variance has been calculated, the standard error can be determined by taking the square root of the variance:  
Once the variance has been calculated, the standard error can be determined by taking the square root of the variance:  


::<math>{{\widehat{se}}_{\widehat{R}}}=\sqrt{\widehat{Var}(\widehat{R}({{t}_{i}}))}</math>
::<math>{{\widehat{se}}_{\widehat{R}}}=\sqrt{\widehat{Var}(\widehat{R}({{t}_{i}}))}\,\!</math>


This information can then be applied to determine the confidence bounds:  
This information can then be applied to determine the confidence bounds:  


::<math>\left[ LC{{B}_{\widehat{R}}},\text{ }UC{{B}_{\widehat{R}}} \right]=\left[ \frac{\widehat{R}}{\widehat{R}+(1-\widehat{R})\cdot w},\text{ }\frac{\widehat{R}}{\widehat{R}+(1-\widehat{R})/w} \right]</math>
::<math>\left[ LC{{B}_{\widehat{R}}},\text{ }UC{{B}_{\widehat{R}}} \right]=\left[ \frac{\widehat{R}}{\widehat{R}+(1-\widehat{R})\cdot w},\text{ }\frac{\widehat{R}}{\widehat{R}+(1-\widehat{R})/w} \right]\,\!</math>


where:  
where:  


::<math>w={{e}^{{{z}_{\alpha }}\cdot \tfrac{{{\widehat{se}}_{\widehat{R}}}}{\left[ \widehat{R}\cdot (1-\widehat{R}) \right]}}}</math>
::<math>w={{e}^{{{z}_{\alpha }}\cdot \tfrac{{{\widehat{se}}_{\widehat{R}}}}{\left[ \widehat{R}\cdot (1-\widehat{R}) \right]}}}\,\!</math>
 
and <math>\alpha\,\!</math> is the desired confidence level for the 1-sided confidence bounds.


and  <math>\alpha </math>  is the desired confidence level for the 1-sided confidence bounds.
===Confidence Bounds Example===


====  Example 12====
Determine the 1-sided confidence bounds for the reliability estimates in the Actuarial-Simple example, with a 95% confidence level.  
Determine the 1-sided confidence bounds for the reliability estimates in Example 11, with a 95% confidence level.
=====  Solution to Example 12=====
Once again, this type of problem is most readily solved by constructing a table similar to the following:


[[Image:lda22.1.gif|thumb|center|400px| ]]
'''Solution'''


Once again, this type of problem is most readily solved by constructing a table similar to the following:


The following plot illustrates these results graphically:
[[Image:Ldat22.1.png|center|800px]]


The following plot illustrates these results graphically:


[[Image:lda22.2.gif|thumb|center|400px| ]]
[[Image:WB.17 nonparametric reliability plot.png|center|550px]] <br>

Latest revision as of 17:15, 23 December 2015

New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images, more targeted search and the latest content available as a PDF. As of September 2023, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest reference at help.reliasoft.com/reference/life_data_analysis

Chapter 17: Non-Parametric Life Data Analysis


Weibullbox.png

Chapter 17  
Non-Parametric Life Data Analysis  

Synthesis-icon.png

Available Software:
Weibull++

Examples icon.png

More Resources:
Weibull++ Examples Collection

Non-parametric analysis allows the user to analyze data without assuming an underlying distribution. This can have certain advantages as well as disadvantages. The ability to analyze data without assuming an underlying life distribution avoids the potentially large errors brought about by making incorrect assumptions about the distribution. On the other hand, the confidence bounds associated with non-parametric analysis are usually much wider than those calculated via parametric analysis, and predictions outside the range of the observations are not possible. Some practitioners recommend that any set of life data should first be subjected to a non-parametric analysis before moving on to the assumption of an underlying distribution.


There are several methods for conducting a non-parametric analysis. In Weibull++, this includes the Kaplan-Meier, actuarial-simple and actuarial-standard methods. A method for attaching confidence bounds to the results of these non-parametric analysis techniques can also be developed. The basis of non-parametric life data analysis is the empirical cdf function, which is given by:


[math]\displaystyle{ \widehat{F}(t)=\frac{observations\le t}{n}\,\! }[/math]


Note that this is similar to the Benard's approximation of the median ranks, as discussed in the Parameter Estimation chapter. The following non-parametric analysis methods are essentially variations of this concept.

Kaplan-Meier Estimator

The Kaplan-Meier estimator, also known as the product limit estimator, can be used to calculate values for non-parametric reliability for data sets with multiple failures and suspensions. The equation of the estimator is given by:

[math]\displaystyle{ \widehat{R}({{t}_{i}})=\underset{j=1}{\overset{i}{\mathop \prod }}\,\frac{{{n}_{j}}-{{r}_{j}}}{{{n}_{j}}},\text{ }i=1,...,m\,\! }[/math]

where:

[math]\displaystyle{ \begin{align} & m= \text{the total number of data points} \\ & n= \text{the total number of units} \end{align}\,\! }[/math]

The variable [math]\displaystyle{ {{n}_{i}}\,\! }[/math] is defined by:

[math]\displaystyle{ {{n}_{i}}=n-\underset{j=0}{\overset{i-1}{\mathop \sum }}\,{{s}_{j}}-\underset{j=0}{\overset{i-1}{\mathop \sum }}\,{{r}_{j,}}\text{ }i=1,...,m\,\! }[/math]

where:

[math]\displaystyle{ \begin{align} & {{r}_{j}}= \text{the number of failures in the }{{j}^{th}}\text{ data group} \\ & {{s}_{j}}= \text{the number of suspensions in the }{{j}^{th}}\text{ data group} \end{align}\,\! }[/math]

Note that the reliability estimate is only calculated for times at which one or more failures occurred. For the sake of calculating the value of [math]\displaystyle{ {{n}_{j}}\,\! }[/math] at time values that have failures and suspensions, it is assumed that the suspensions occur slightly after the failures, so that the suspended units are considered to be operating and included in the count of [math]\displaystyle{ {{n}_{j}}\,\! }[/math].

Kaplan-Meier Example

A group of 20 units are put on a life test with the following results.

[math]\displaystyle{ \begin{matrix} Number & State & State \\ in State & (F or S) & End Time \\ 3 & F & 9 \\ 1 & S & 9 \\ 1 & F & 11 \\ 1 & S & 12 \\ 1 & F & 13 \\ 1 & S & 13 \\ 1 & S & 15 \\ 1 & F & 17 \\ 1 & F & 21 \\ 1 & S & 22 \\ 1 & S & 24 \\ 1 & S & 26 \\ 1 & F & 28 \\ 1 & F & 30 \\ 1 & S & 32 \\ 2 & S & 35 \\ 1 & S & 39 \\ 1 & S & 41 \\ \end{matrix}\,\! }[/math]

Use the Kaplan-Meier estimator to determine the reliability estimates for each failure time.

Solution

Using the data and the reliability equation of the Kaplan-Meier estimator, the following table can be constructed:

[math]\displaystyle{ \begin{matrix} State & Number of & Number of & Available & {} & {} \\ End Time & Failures, {{r}_{i}} & Suspensions, {{s}_{i}} & Units, {{n}_{i}} & \tfrac{{{n}_{i}}-{{r}_{i}}}{{{n}_{i}}} & \mathop{}_{}^{}\prod\tfrac{{{n}_{i}}-{{r}_{i}}}{{{n}_{i}}} \\ 9 & 3 & 1 & 20 & 0.850 & 0.850 \\ 11 & 1 & 0 & 16 & 0.938 & 0.797 \\ 12 & 0 & 1 & 15 & 1.000 & 0.797 \\ 13 & 1 & 1 & 14 & 0.929 & 0.740 \\ 15 & 0 & 1 & 12 & 1.000 & 0.740 \\ 17 & 1 & 0 & 11 & 0.909 & 0.673 \\ 21 & 1 & 0 & 10 & 0.900 & 0.605 \\ 22 & 0 & 1 & 9 & 1.000 & 0.605 \\ 24 & 0 & 1 & 8 & 1.000 & 0.605 \\ 26 & 0 & 1 & 7 & 1.000 & 0.605 \\ 28 & 1 & 0 & 6 & 0.833 & 0.505 \\ 30 & 1 & 0 & 5 & 0.800 & 0.404 \\ 32 & 0 & 1 & 4 & 1.000 & 0.404 \\ 35 & 0 & 1 & 3 & 1.000 & 0.404 \\ 39 & 0 & 1 & 2 & 1.000 & 0.404 \\ 41 & 0 & 1 & 1 & 1.000 & 0.404 \\ \end{matrix}\,\! }[/math]

As can be determined from the preceding table, the reliability estimates for the failure times are:

[math]\displaystyle{ \begin{matrix} Failure Time & Reliability Est. \\ 9 & 85.0% \\ 11 & 79.7% \\ 13 & 74.0% \\ 17 & 67.3% \\ 21 & 60.5% \\ 28 & 50.5% \\ 30 & 40.4% \\ \end{matrix}\,\! }[/math]

Actuarial-Simple Method

The actuarial-simple method is an easy-to-use form of non-parametric data analysis that can be used for multiple censored data that are arranged in intervals. This method is based on calculating the number of failures in a time interval, [math]\displaystyle{ {{r}_{j}}\,\! }[/math] versus the number of operating units in that time period, [math]\displaystyle{ {{n}_{j}}\,\! }[/math]. The equation for the reliability estimator for the standard actuarial method is given by:

[math]\displaystyle{ \widehat{R}({{t}_{i}})=\underset{j=1}{\overset{i}{\mathop \prod }}\,\left( 1-\frac{{{r}_{j}}}{{{n}_{j}}} \right),\text{ }i=1,...,m\,\! }[/math]

where:

[math]\displaystyle{ \begin{align} & m= \text{the total number of intervals} \\ & n= \text{the total number of units} \end{align}\,\! }[/math]

The variable [math]\displaystyle{ {{n}_{i}}\,\! }[/math] is defined by:

[math]\displaystyle{ {{n}_{i}}=n-\underset{j=0}{\overset{i-1}{\mathop \sum }}\,{{s}_{j}}-\underset{j=0}{\overset{i-1}{\mathop \sum }}\,{{r}_{j,}}\text{ }i=1,...,m\,\! }[/math]

where:

[math]\displaystyle{ \begin{align} & {{r}_{j}}= \text{the number of failures in interval }j \\ & {{s}_{j}}= \text{the number of suspensions in interval }j \end{align}\,\! }[/math]

Actuarial-Simple Example

A group of 55 units are put on a life test during which the units are evaluated every 50 hours. The results are:

[math]\displaystyle{ \begin{matrix} Start & End & Number of & Number of \\ Time & Time & Failures, {{r}_{i}} & Suspensions, {{s}_{i}} \\ 0 & 50 & 2 & 4 \\ 50 & 100 & 0 & 5 \\ 100 & 150 & 2 & 2 \\ 150 & 200 & 3 & 5 \\ 200 & 250 & 2 & 1 \\ 250 & 300 & 1 & 2 \\ 300 & 350 & 2 & 1 \\ 350 & 400 & 3 & 3 \\ 400 & 450 & 3 & 4 \\ 450 & 500 & 1 & 2 \\ 500 & 550 & 2 & 1 \\ 550 & 600 & 1 & 0 \\ 600 & 650 & 2 & 1 \\ \end{matrix}\,\! }[/math]

Solution

The reliability estimates can be obtained by expanding the data table to include the calculations used in the actuarial-simple method:

[math]\displaystyle{ \begin{matrix} Start & End & Number of & Number of & Available & {} & {} \\ Time & Time & Failures, {{r}_{i}} & Suspensions, {{s}_{i}} & Units, {{n}_{i}} & 1-\tfrac{{{r}_{j}}}{{{n}_{j}}} & \prod\mathop{}_{}^{}1-\tfrac{{{r}_{j}}}{{{n}_{j}}} \\ 0 & 50 & 2 & 4 & 55 & 0.964 & 0.964 \\ 50 & 100 & 0 & 5 & 49 & 1.000 & 0.964 \\ 100 & 150 & 2 & 2 & 44 & 0.955 & 0.920 \\ 150 & 200 & 3 & 5 & 40 & 0.925 & 0.851 \\ 200 & 250 & 2 & 1 & 32 & 0.938 & 0.798 \\ 250 & 300 & 1 & 2 & 29 & 0.966 & 0.770 \\ 300 & 350 & 2 & 1 & 26 & 0.923 & 0.711 \\ 350 & 400 & 3 & 3 & 23 & 0.870 & 0.618 \\ 400 & 450 & 3 & 4 & 17 & 0.824 & 0.509 \\ 450 & 500 & 1 & 2 & 10 & 0.900 & 0.458 \\ 500 & 550 & 2 & 1 & 7 & 0.714 & 0.327 \\ 550 & 600 & 1 & 0 & 4 & 0.750 & 0.245 \\ 600 & 650 & 2 & 1 & 3 & 0.333 & 0.082 \\ \end{matrix}\,\! }[/math]

As can be determined from the preceding table, the reliability estimates for the failure times are:

[math]\displaystyle{ \begin{matrix} Failure Period & Reliability \\ End Time & Estimate \\ 50 & 96.4% \\ 150 & 92.0% \\ 200 & 85.1% \\ 250 & 79.8% \\ 300 & 77.0% \\ 350 & 71.1% \\ 400 & 61.8% \\ 450 & 50.9% \\ 500 & 45.8% \\ 550 & 32.7% \\ 600 & 24.5% \\ 650 & 8.2% \\ \end{matrix}\,\! }[/math]

Actuarial-Standard Method

The actuarial-standard model is a variation of the actuarial-simple model. In the actuarial-simple method, the suspensions in a time period or interval are assumed to occur at the end of that interval, after the failures have occurred. The actuarial-standard model assumes that the suspensions occur in the middle of the interval, which has the effect of reducing the number of available units in the interval by half of the suspensions in that interval or:

[math]\displaystyle{ n_{i}^{\prime }={{n}_{i}}-\frac{{{s}_{i}}}{2}\,\! }[/math]

With this adjustment, the calculations are carried out just as they were for the actuarial-simple model or:

[math]\displaystyle{ \widehat{R}({{t}_{i}})=\underset{j=1}{\overset{i}{\mathop \prod }}\,\left( 1-\frac{{{r}_{j}}}{n_{j}^{\prime }} \right),\text{ }i=1,...,m\,\! }[/math]

Actuarial-Standard Example

Use the data set from the Actuarial-Simple example and analyze it using the actuarial-standard method.

Solution

The solution to this example is similar to that in the Actuarial-Simple example, with the exception of the inclusion of the [math]\displaystyle{ n_{i}^{\prime }\,\! }[/math] term, which is used in the equation for the actuarial-standard method. Applying this equation to the data, we can generate the following table:

[math]\displaystyle{ \begin{matrix} Start & End & Number of & Number of & Adjusted & {} & {} \\ Time & Time & Failures, {{r}_{i}} & Suspensions, {{s}_{i}} & Units, n_{i}^{\prime } & 1-\tfrac{{{r}_{j}}}{n_{j}^{\prime }} & \prod\mathop{}_{}^{}1-\tfrac{{{r}_{j}}}{n_{j}^{\prime }} \\ 0 & 50 & 2 & 4 & 53 & 0.962 & 0.962 \\ 50 & 100 & 0 & 5 & 46.5 & 1.000 & 0.962 \\ 100 & 150 & 2 & 2 & 43 & 0.953 & 0.918 \\ 150 & 200 & 3 & 5 & 37.5 & 0.920 & 0.844 \\ 200 & 250 & 2 & 1 & 31.5 & 0.937 & 0.791 \\ 250 & 300 & 1 & 2 & 28 & 0.964 & 0.762 \\ 300 & 350 & 2 & 1 & 25.5 & 0.922 & 0.702 \\ 350 & 400 & 3 & 3 & 21.5 & 0.860 & 0.604 \\ 400 & 450 & 3 & 4 & 15 & 0.800 & 0.484 \\ 450 & 500 & 1 & 2 & 9 & 0.889 & 0.430 \\ 500 & 550 & 2 & 1 & 6.5 & 0.692 & 0.298 \\ 550 & 600 & 1 & 0 & 4 & 0.750 & 0.223 \\ 600 & 650 & 2 & 1 & 2.5 & 0.200 & 0.045 \\ \end{matrix}\,\! }[/math]

As can be determined from the preceding table, the reliability estimates for the failure times are:

[math]\displaystyle{ \begin{matrix} Failure Period & Reliability \\ End Time & Estimate \\ 50 & 96.2% \\ 150 & 91.8% \\ 200 & 84.4% \\ 250 & 79.1% \\ 300 & 76.2% \\ 350 & 70.2% \\ 400 & 60.4% \\ 450 & 48.4% \\ 500 & 43.0% \\ 550 & 29.8% \\ 600 & 22.3% \\ 650 & 4.5% \\ \end{matrix}\,\! }[/math]

Non-Parametric Confidence Bounds

Confidence bounds for non-parametric reliability estimates can be calculated using a method similar to that of parametric confidence bounds. The difficulty in dealing with nonparametric data lies in the estimation of the variance. To estimate the variance for non-parametric data, Weibull++ uses Greenwood's formula [27]:

[math]\displaystyle{ \widehat{Var}(\hat{R}({{t}_{i}}))={{\left[ \hat{R}({{t}_{i}}) \right]}^{2}}\cdot \underset{j=1}{\overset{i}{\mathop \sum }}\,\frac{\tfrac{{{r}_{j}}}{{{n}_{j}}}}{{{n}_{j}}\cdot \left( 1-\tfrac{{{r}_{j}}}{{{n}_{j}}} \right)}\,\! }[/math]

where:

[math]\displaystyle{ \begin{align} & m= \text{ the total number of intervals} \\ & n= \text{ the total number of units} \end{align}\,\! }[/math]

The variable [math]\displaystyle{ {{n}_{i}}\,\! }[/math] is defined by:

[math]\displaystyle{ {{n}_{i}}=n-\underset{j=0}{\overset{i-1}{\mathop \sum }}\,{{s}_{j}}-\underset{j=0}{\overset{i-1}{\mathop \sum }}\,{{r}_{j,}}\text{ }i=1,...,m\,\! }[/math]

where:

[math]\displaystyle{ \begin{align} & {{r}_{j}}= \text{the number of failures in interval }j \\ & {{s}_{j}}= \text{the number of suspensions in interval }j \end{align}\,\! }[/math]

Once the variance has been calculated, the standard error can be determined by taking the square root of the variance:

[math]\displaystyle{ {{\widehat{se}}_{\widehat{R}}}=\sqrt{\widehat{Var}(\widehat{R}({{t}_{i}}))}\,\! }[/math]

This information can then be applied to determine the confidence bounds:

[math]\displaystyle{ \left[ LC{{B}_{\widehat{R}}},\text{ }UC{{B}_{\widehat{R}}} \right]=\left[ \frac{\widehat{R}}{\widehat{R}+(1-\widehat{R})\cdot w},\text{ }\frac{\widehat{R}}{\widehat{R}+(1-\widehat{R})/w} \right]\,\! }[/math]

where:

[math]\displaystyle{ w={{e}^{{{z}_{\alpha }}\cdot \tfrac{{{\widehat{se}}_{\widehat{R}}}}{\left[ \widehat{R}\cdot (1-\widehat{R}) \right]}}}\,\! }[/math]

and [math]\displaystyle{ \alpha\,\! }[/math] is the desired confidence level for the 1-sided confidence bounds.

Confidence Bounds Example

Determine the 1-sided confidence bounds for the reliability estimates in the Actuarial-Simple example, with a 95% confidence level.

Solution

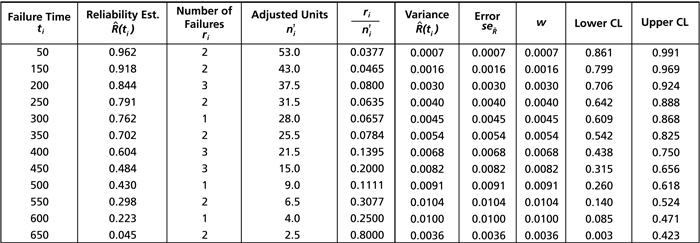
Once again, this type of problem is most readily solved by constructing a table similar to the following:

Ldat22.1.png

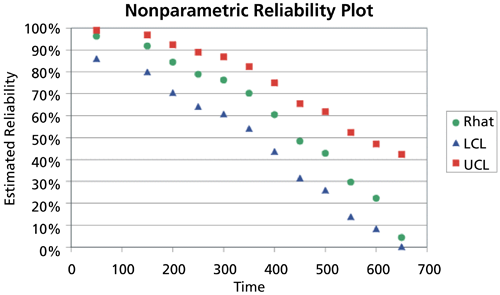
The following plot illustrates these results graphically:

WB.17 nonparametric reliability plot.png


Retrieved from "https://www.reliawiki.com/index.php?title=Non-Parametric_Life_Data_Analysis&oldid=62260"