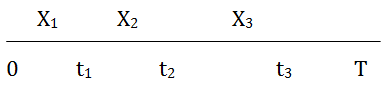Repairable Systems Analysis
Data from systems in the field can be analyzed in the RGA software. This type of data is called fielded systems data and is analogous to warranty data. Fielded systems can be categorized into two basic types: one-time or non-repairable systems, and reusable or repairable systems. In the latter case, under continuous operation, the system is repaired, but not replaced after each failure. For example, if a water pump in a vehicle fails, the water pump is replaced and the vehicle is repaired.
This chapter presents repairable systems analysis, where the reliability of a system can be tracked and quantified based on data from multiple systems in the field. The next chapter will present fleet analysis, where data from multiple systems in the field can be collected and analyzed so that reliability metrics for the fleet as a whole can be quantified.
Background
Most complex systems, such as automobiles, communication systems, aircraft, printers, medical diagnostics systems, helicopters, etc., are repaired and not replaced when they fail. When these systems are fielded or subjected to a customer use environment, it is often of considerable interest to determine the reliability and other performance characteristics under these conditions. Areas of interest may include assessing the expected number of failures during the warranty period, maintaining a minimum mission reliability, evaluating the rate of wearout, determining when to replace or overhaul a system and minimizing life cycle costs. In general, a lifetime distribution, such as the Weibull distribution, cannot be used to address these issues. In order to address the reliability characteristics of complex repairable systems, a process is often used instead of a distribution. The most popular process model is the Power Law model. This model is popular for several reasons. One is that it has a very practical foundation in terms of minimal repair, which is a situation where the repair of a failed system is just enough to get the system operational again. Second, if the time to first failure follows the Weibull distribution, then each succeeding failure is governed by the Power Law model as in the case of minimal repair. From this point of view, the Power Law model is an extension of the Weibull distribution.
Sometimes, the Crow Extended model, which was introduced in a previous chapter for analyzing developmental data, is also applied for fielded repairable systems. Applying the Crow Extended model on repairable system data allows analysts to project the system MTBF after reliability-related issues are addressed during the field operation. Projections are calculated based on the mode classifications (A, BC and BD). The calculation procedure is the same as the one for the developmental data, and is not repeated in this chapter.
Distribution Example
Visualize a socket into which a component is inserted at time 0. When the component fails, it is replaced immediately with a new one of the same kind. After each replacement, the socket is put back into an as good as new condition. Each component has a time-to-failure that is determined by the underlying distribution. It is important to note that a distribution relates to a single failure. The sequence of failures for the socket constitutes a random process called a renewal process. In the illustration below, the component life is [math]\displaystyle{ {{X}_{j}}\,\! }[/math], and [math]\displaystyle{ {{t}_{j}}\,\! }[/math] is the system time to the [math]\displaystyle{ {{j}^{th}}\,\! }[/math] failure.
Each component life [math]\displaystyle{ {{X}_{j}}\,\! }[/math] in the socket is governed by the same distribution [math]\displaystyle{ F(x)\,\! }[/math].
A distribution, such as Weibull, governs a single lifetime. There is only one event associated with a distribution. The distribution [math]\displaystyle{ F(x)\,\! }[/math] is the probability that the life of the component in the socket is less than [math]\displaystyle{ x\,\! }[/math]. In the illustration above, [math]\displaystyle{ {{X}_{1}}\,\! }[/math] is the life of the first component in the socket. [math]\displaystyle{ F(x)\,\! }[/math] is the probability that the first component in the socket fails in time [math]\displaystyle{ x\,\! }[/math]. When the first component fails, it is replaced in the socket with a new component of the same type. The probability that the life of the second component is less than [math]\displaystyle{ x\,\! }[/math] is given by the same distribution function, [math]\displaystyle{ F(x)\,\! }[/math]. For the Weibull distribution:
- [math]\displaystyle{ F(x)=1-{{e}^{-\lambda {{x}^{\beta }}}}\,\! }[/math]
A distribution is also characterized by its density function, such that:
- [math]\displaystyle{ f(x)=\frac{d}{dx}F(x)\,\! }[/math]
The density function for the Weibull distribution is:
- [math]\displaystyle{ f(x)=\lambda \beta {{x}^{\beta -1}}\cdot {{e}^{-\lambda \beta x}}\,\! }[/math]
In addition, an important reliability property of a distribution function is the failure rate, which is given by:
- [math]\displaystyle{ r(x)=\frac{f(x)}{1-F(x)}\,\! }[/math]
The interpretation of the failure rate is that for a small interval of time [math]\displaystyle{ \Delta x\,\! }[/math], [math]\displaystyle{ r(x)\Delta x\,\! }[/math] is approximately the probability that a component in the socket will fail between time [math]\displaystyle{ x\,\! }[/math] and time [math]\displaystyle{ x+\Delta x\,\! }[/math], given that the component has not failed by time [math]\displaystyle{ x\,\! }[/math]. For the Weibull distribution, the failure rate is given by:
- [math]\displaystyle{ \begin{align} r(x)=\lambda \beta {{x}^{\beta -1}} \end{align}\,\! }[/math]
It is important to note the condition that the component has not failed by time [math]\displaystyle{ x\,\! }[/math]. Again, a distribution deals with one lifetime of a component and does not allow for more than one failure. The socket has many failures and each failure time is individually governed by the same distribution. In other words, the failure times are independent of each other. If the failure rate is increasing, then this is indicative of component wearout. If the failure rate is decreasing, then this is indicative of infant mortality. If the failure rate is constant, then the component failures follow an exponential distribution. For the Weibull distribution, the failure rate is increasing for [math]\displaystyle{ \beta \gt 1\,\! }[/math], decreasing for [math]\displaystyle{ \beta\lt 1\,\! }[/math] and constant for [math]\displaystyle{ \beta =1\,\! }[/math]. Each time a component in the socket is replaced, the failure rate of the new component goes back to the value at time 0. This means that the socket is as good as new after each failure and each subsequent replacement by a new component. This process is continued for the operation of the socket.
Process Example
Now suppose that a system consists of many components with each component in a socket. A failure in any socket constitutes a failure of the system. Each component in a socket is a renewal process governed by its respective distribution function. When the system fails due to a failure in a socket, the component is replaced and the socket is again as good as new. The system has been repaired. Because there are many other components still operating with various ages, the system is not typically put back into a like new condition after the replacement of a single component. For example, a car is not as good as new after the replacement of a failed water pump. Therefore, distribution theory does not apply to the failures of a complex system, such as a car. In general, the intervals between failures for a complex repairable system do not follow the same distribution. Distributions apply to the components that are replaced in the sockets, but not at the system level. At the system level, a distribution applies to the very first failure. There is one failure associated with a distribution. For example, the very first system failure may follow a Weibull distribution.
For many systems in a real world environment, a repair may only be enough to get the system operational again. If the water pump fails on the car, the repair consists only of installing a new water pump. Similarly, if a seal leaks, the seal is replaced but no additional maintenance is done. This is the concept of minimal repair. For a system with many failure modes, the repair of a single failure mode does not greatly improve the system reliability from what it was just before the failure. Under minimal repair for a complex system with many failure modes, the system reliability after a repair is the same as it was just before the failure. In this case, the sequence of failures at the system level follows a non-homogeneous Poisson process (NHPP).
The system age when the system is first put into service is time 0. Under the NHPP, the first failure is governed by a distribution [math]\displaystyle{ F(x)\,\! }[/math] with failure rate [math]\displaystyle{ r(x)\,\! }[/math]. Each succeeding failure is governed by the intensity function [math]\displaystyle{ u(t)\,\! }[/math] of the process. Let [math]\displaystyle{ t\,\! }[/math] be the age of the system and [math]\displaystyle{ \Delta t\,\! }[/math] is very small. The probability that a system of age [math]\displaystyle{ t\,\! }[/math] fails between [math]\displaystyle{ t\,\! }[/math] and [math]\displaystyle{ t+\Delta t\,\! }[/math] is given by the intensity function [math]\displaystyle{ u(t)\Delta t\,\! }[/math]. Notice that this probability is not conditioned on not having any system failures up to time [math]\displaystyle{ t\,\! }[/math], as is the case for a failure rate. The failure intensity [math]\displaystyle{ u(t)\,\! }[/math] for the NHPP has the same functional form as the failure rate governing the first system failure. Therefore, [math]\displaystyle{ u(t)=r(t)\,\! }[/math], where [math]\displaystyle{ r(t)\,\! }[/math] is the failure rate for the distribution function of the first system failure. If the first system failure follows the Weibull distribution, the failure rate is:
- [math]\displaystyle{ \begin{align} r(x)=\lambda \beta {{x}^{\beta -1}} \end{align}\,\! }[/math]
Under minimal repair, the system intensity function is:
- [math]\displaystyle{ \begin{align} u(t)=\lambda \beta {{t}^{\beta -1}} \end{align}\,\! }[/math]
This is the Power Law model. It can be viewed as an extension of the Weibull distribution. The Weibull distribution governs the first system failure, and the Power Law model governs each succeeding system failure. If the system has a constant failure intensity [math]\displaystyle{ u(t) = \lambda \,\! }[/math], then the intervals between system failures follow an exponential distribution with failure rate [math]\displaystyle{ \lambda \,\! }[/math]. If the system operates for time [math]\displaystyle{ T\,\! }[/math], then the random number of failures [math]\displaystyle{ N(T)\,\! }[/math] over 0 to [math]\displaystyle{ T\,\! }[/math] is given by the Power Law mean value function.
- [math]\displaystyle{ \begin{align} E[N(T)]=\lambda {{T}^{\beta }} \end{align}\,\! }[/math]
Therefore, the probability [math]\displaystyle{ N(T)=n\,\! }[/math] is given by the Poisson probability.
- [math]\displaystyle{ \frac{{{\left( \lambda T \right)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2\ldots \,\! }[/math]
This is referred to as a homogeneous Poisson process because there is no change in the intensity function. This is a special case of the Power Law model for [math]\displaystyle{ \beta =1\,\! }[/math]. The Power Law model is a generalization of the homogeneous Poisson process and allows for change in the intensity function as the repairable system ages. For the Power Law model, the failure intensity is increasing for [math]\displaystyle{ \beta \gt 1\,\! }[/math] (wearout), decreasing for [math]\displaystyle{ \beta \lt 1\,\! }[/math] (infant mortality) and constant for [math]\displaystyle{ \beta =1\,\! }[/math] (useful life).
Power Law Model
The Power Law model is often used to analyze the reliability of complex repairable systems in the field. The system of interest may be the total system, such as a helicopter, or it may be subsystems, such as the helicopter transmission or rotator blades. When these systems are new and first put into operation, the start time is 0. As these systems are operated, they accumulate age (e.g., miles on automobiles, number of pages on copiers, flights of helicopters). When these systems fail, they are repaired and put back into service.
Some system types may be overhauled and some may not, depending on the maintenance policy. For example, an automobile may not be overhauled but helicopter transmissions may be overhauled after a period of time. In practice, an overhaul may not convert the system reliability back to where it was when the system was new. However, an overhaul will generally make the system more reliable. Appropriate data for the Power Law model is over cycles. If a system is not overhauled, then there is only one cycle and the zero time is when the system is first put into operation. If a system is overhauled, then the same serial number system may generate many cycles. Each cycle will start a new zero time, the beginning of the cycle. The age of the system is from the beginning of the cycle. For systems that are not overhauled, there is only one cycle and the reliability characteristics of a system as the system ages during its life is of interest. For systems that are overhauled, you are interested in the reliability characteristics of the system as it ages during its cycle.
For the Power Law model, a data set for a system will consist of a starting time [math]\displaystyle{ S\,\! }[/math], an ending time [math]\displaystyle{ T\,\! }[/math] and the accumulated ages of the system during the cycle when it had failures. Assume that the data exists from the beginning of a cycle (i.e., the starting time is 0), although non-zero starting times are possible with the Power Law model. For example, suppose data has been collected for a system with 2,000 hours of operation during a cycle. The starting time is [math]\displaystyle{ S=0\,\! }[/math] and the ending time is [math]\displaystyle{ T=2000\,\! }[/math]. Over this period, failures occurred at system ages of 50.6, 840.7, 1060.5, 1186.5, 1613.6 and 1843.4 hours. These are the accumulated operating times within the cycle, and there were no failures between 1843.4 and 2000 hours. It may be of interest to determine how the systems perform as part of a fleet. For a fleet, it must be verified that the systems have the same configuration, same maintenance policy and same operational environment. In this case, a random sample must be gathered from the fleet. Each item in the sample will have a cycle starting time [math]\displaystyle{ S=0\,\! }[/math], an ending time [math]\displaystyle{ T\,\! }[/math] for the data period and the accumulated operating times during this period when the system failed.
There are many ways to generate a random sample of [math]\displaystyle{ K\,\! }[/math] systems. One way is to generate [math]\displaystyle{ K\,\! }[/math] random serial numbers from the fleet. Then go to the records corresponding to the randomly selected systems. If the systems are not overhauled, then record when each system was first put into service. For example, the system may have been put into service when the odometer mileage equaled zero. Each system may have a different amount of total usage, so the ending times, [math]\displaystyle{ T\,\! }[/math], may be different. If the systems are overhauled, then the records for the last completed cycle will be needed. The starting and ending times and the accumulated times to failure for the [math]\displaystyle{ K\,\! }[/math] systems constitute the random sample from the fleet. There is a useful and efficient method for generating a random sample for systems that are overhauled. If the overhauled systems have been in service for a considerable period of time, then each serial number system in the fleet would go through many overhaul cycles. In this case, the systems coming in for overhaul actually represent a random sample from the fleet. As [math]\displaystyle{ K\,\! }[/math] systems come in for overhaul, the data for the current completed cycles would be a random sample of size [math]\displaystyle{ K\,\! }[/math].
In addition, the warranty period may be of particular interest. In this case, randomly choose [math]\displaystyle{ K\,\! }[/math] serial numbers for systems that have been in customer use for a period longer than the warranty period. Then check the warranty records. For each of the [math]\displaystyle{ K\,\! }[/math] systems that had warranty work, the ages corresponding to this service are the failure times. If a system did not have warranty work, then the number of failures recorded for that system is zero. The starting times are all equal to zero and the ending time for each of the [math]\displaystyle{ K\,\! }[/math] systems is equal to the warranty operating usage time (e.g., hours, copies, miles).
In addition to the intensity function [math]\displaystyle{ u(t)\,\! }[/math] and the mean value function, which were given in the section above, other relationships based on the Power Law are often of practical interest. For example, the probability that the system will survive to age [math]\displaystyle{ t+d\,\! }[/math] without failure is given by:
- [math]\displaystyle{ R(t)={{e}^{-\left[ \lambda {{\left( t+d \right)}^{\beta }}-\lambda {{t}^{\beta }} \right]}}\,\! }[/math]
This is the mission reliability for a system of age [math]\displaystyle{ t\,\! }[/math] and mission length [math]\displaystyle{ d\,\! }[/math].
Parameter Estimation
Suppose that the number of systems under study is [math]\displaystyle{ K\,\! }[/math] and the [math]\displaystyle{ {{q}^{th}}\,\! }[/math] system is observed continuously from time [math]\displaystyle{ {{S}_{q}}\,\! }[/math] to time [math]\displaystyle{ {{T}_{q}}\,\! }[/math], [math]\displaystyle{ q=1,2,\ldots ,K\,\! }[/math]. During the period [math]\displaystyle{ [{{S}_{q}},{{T}_{q}}]\,\! }[/math], let [math]\displaystyle{ {{N}_{q}}\,\! }[/math] be the number of failures experienced by the [math]\displaystyle{ {{q}^{th}}\,\! }[/math] system and let [math]\displaystyle{ {{X}_{i,q}}\,\! }[/math] be the age of this system at the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] occurrence of failure, [math]\displaystyle{ i=1,2,\ldots ,{{N}_{q}}\,\! }[/math]. It is also possible that the times [math]\displaystyle{ {{S}_{q}}\,\! }[/math] and [math]\displaystyle{ {{T}_{q}}\,\! }[/math] may be the observed failure times for the [math]\displaystyle{ {{q}^{th}}\,\! }[/math] system. If [math]\displaystyle{ {{X}_{{{N}_{q}},q}}={{T}_{q}}\,\! }[/math], then the data on the [math]\displaystyle{ {{q}^{th}}\,\! }[/math] system is said to be failure terminated, and [math]\displaystyle{ {{T}_{q}}\,\! }[/math] is a random variable with [math]\displaystyle{ {{N}_{q}}\,\! }[/math] fixed. If [math]\displaystyle{ {{X}_{{{N}_{q}},q}}\lt {{T}_{q}}\,\! }[/math], then the data on the [math]\displaystyle{ {{q}^{th}}\,\! }[/math] system is said to be time terminated with [math]\displaystyle{ {{N}_{q}}\,\! }[/math] a random variable. The maximum likelihood estimates of [math]\displaystyle{ \lambda \,\! }[/math] and [math]\displaystyle{ \beta \,\! }[/math] are values satisfying the equations shown next.
- [math]\displaystyle{ \begin{align} \widehat{\lambda }= & \frac{\underset{q=1}{\overset{K}{\mathop{\sum }}}\,{{N}_{q}}}{\underset{q=1}{\overset{K}{\mathop{\sum }}}\,\left( T_{q}^{\widehat{\beta }}-S_{q}^{\widehat{\beta }} \right)} \\ \widehat{\beta }= & \frac{\underset{q=1}{\overset{K}{\mathop{\sum }}}\,{{N}_{q}}}{\widehat{\lambda }\underset{q=1}{\overset{K}{\mathop{\sum }}}\,\left[ T_{q}^{\widehat{\beta }}\ln ({{T}_{q}})-S_{q}^{\widehat{\beta }}\ln ({{S}_{q}}) \right]-\underset{q=1}{\overset{K}{\mathop{\sum }}}\,\underset{i=1}{\overset{{{N}_{q}}}{\mathop{\sum }}}\,\ln ({{X}_{i,q}})} \end{align}\,\! }[/math]
where [math]\displaystyle{ 0\ln 0\,\! }[/math] is defined to be 0. In general, these equations cannot be solved explicitly for [math]\displaystyle{ \widehat{\lambda }\,\! }[/math] and [math]\displaystyle{ \widehat{\beta },\,\! }[/math] but must be solved by iterative procedures. Once [math]\displaystyle{ \widehat{\lambda }\,\! }[/math] and [math]\displaystyle{ \widehat{\beta }\,\! }[/math] have been estimated, the maximum likelihood estimate of the intensity function is given by:
- [math]\displaystyle{ \widehat{u}(t)=\widehat{\lambda }\widehat{\beta }{{t}^{\widehat{\beta }-1}}\,\! }[/math]
If [math]\displaystyle{ {{S}_{1}}={{S}_{2}}=\ldots ={{S}_{q}}=0\,\! }[/math] and [math]\displaystyle{ {{T}_{1}}={{T}_{2}}=\ldots ={{T}_{q}}\,\! }[/math] [math]\displaystyle{ \,(q=1,2,\ldots ,K)\,\! }[/math] then the maximum likelihood estimates [math]\displaystyle{ \widehat{\lambda }\,\! }[/math] and [math]\displaystyle{ \widehat{\beta }\,\! }[/math] are in closed form.
- [math]\displaystyle{ \begin{align} \widehat{\lambda }= & \frac{\underset{q=1}{\overset{K}{\mathop{\sum }}}\,{{N}_{q}}}{K{{T}^{\beta }}} \\ \widehat{\beta }= & \frac{\underset{q=1}{\overset{K}{\mathop{\sum }}}\,{{N}_{q}}}{\underset{q=1}{\overset{K}{\mathop{\sum }}}\,\underset{i=1}{\overset{{{N}_{q}}}{\mathop{\sum }}}\,\ln (\tfrac{T}{{{X}_{iq}}})} \end{align}\,\! }[/math]
The following example illustrates these estimation procedures.
Power Law Model Example
For the data in the following table, the starting time for each system is equal to 0 and the ending time for each system is 2,000 hours. Calculate the maximum likelihood estimates [math]\displaystyle{ \widehat{\lambda }\,\! }[/math] and [math]\displaystyle{ \widehat{\beta }\,\! }[/math].
| Repairable System Failure Data | ||
| System 1 ( [math]\displaystyle{ {{X}_{i1}}\,\! }[/math] ) | System 2 ( [math]\displaystyle{ {{X}_{i2}}\,\! }[/math] ) | System 3 ( [math]\displaystyle{ {{X}_{i3}}\,\! }[/math] ) |
|---|---|---|
| 1.2 | 1.4 | 0.3 |
| 55.6 | 35.0 | 32.6 |
| 72.7 | 46.8 | 33.4 |
| 111.9 | 65.9 | 241.7 |
| 121.9 | 181.1 | 396.2 |
| 303.6 | 712.6 | 444.4 |
| 326.9 | 1005.7 | 480.8 |
| 1568.4 | 1029.9 | 588.9 |
| 1913.5 | 1675.7 | 1043.9 |
| 1787.5 | 1136.1 | |
| 1867.0 | 1288.1 | |
| 1408.1 | ||
| 1439.4 | ||
| 1604.8 | ||
| [math]\displaystyle{ {{N}_{1}}=9\,\! }[/math] | [math]\displaystyle{ {{N}_{2}}=11\,\! }[/math] | [math]\displaystyle{ {{N}_{3}}=14\,\! }[/math] |
Solution
Because the starting time for each system is equal to zero and each system has an equivalent ending time, the general equations for [math]\displaystyle{ \widehat{\beta }\,\! }[/math] and [math]\displaystyle{ \widehat{\lambda }\,\! }[/math] reduce to the closed form equations. The maximum likelihood estimates of [math]\displaystyle{ \hat{\beta }\,\! }[/math] and [math]\displaystyle{ \hat{\lambda }\,\! }[/math] are then calculated as follows:
- [math]\displaystyle{ \widehat{\beta }= \frac{\underset{q=1}{\overset{K}{\mathop{\sum }}}\,{{N}_{q}}}{\underset{q=1}{\overset{K}{\mathop{\sum }}}\,\underset{i=1}{\overset{{{N}_{q}}}{\mathop{\sum }}}\,\ln (\tfrac{T}{{{X}_{iq}}})} = 0.45300 }[/math]
- [math]\displaystyle{ \widehat{\lambda }= \frac{\underset{q=1}{\overset{K}{\mathop{\sum }}}\,{{N}_{q}}}{K{{T}^{\beta }}} = 0.36224 \,\! }[/math]
The system failure intensity function is then estimated by:
- [math]\displaystyle{ \widehat{u}(t)=\widehat{\lambda }\widehat{\beta }{{t}^{\widehat{\beta }-1}},\text{ }t\gt 0\,\! }[/math]
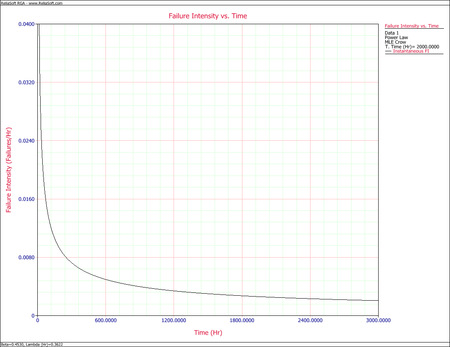
The next figure is a plot of [math]\displaystyle{ \widehat{u}(t)\,\! }[/math] over the period (0, 3000). Clearly, the estimated failure intensity function is most representative over the range of the data and any extrapolation should be viewed with the usual caution.
Goodness-of-Fit Tests for Repairable System Analysis
It is generally desirable to test the compatibility of a model and data by a statistical goodness-of-fit test. A parametric Cramér-von Mises goodness-of-fit test is used for the multiple system and repairable system Power Law model, as proposed by Crow in [17]. This goodness-of-fit test is appropriate whenever the start time for each system is 0 and the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}]\,\! }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances. In addition, the Common Beta Hypothesis test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}}\,\! }[/math] values of each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared goodness-of-fit tests are illustrated next.
Cramér-von Mises Test
To illustrate the application of the Cramér-von Mises statistic for multiple systems data, suppose that [math]\displaystyle{ K\,\! }[/math] like systems are under study and you wish to test the hypothesis [math]\displaystyle{ {{H}_{1}}\,\! }[/math] that their failure times follow a non-homogeneous Poisson process. Suppose information is available for the [math]\displaystyle{ {{q}^{th}}\,\! }[/math] system over the interval [math]\displaystyle{ [0,{{T}_{q}}]\,\! }[/math], with successive failure times , [math]\displaystyle{ (q=1,2,\ldots ,\,K)\,\! }[/math]. The Cramér-von Mises test can be performed with the following steps:
Step 1: If [math]\displaystyle{ {{x}_{{{N}_{q}}q}}={{T}_{q}}\,\! }[/math] (failure terminated), let [math]\displaystyle{ {{M}_{q}}={{N}_{q}}-1\,\! }[/math], and if [math]\displaystyle{ {{x}_{{{N}_{q}}q}}\lt T\,\! }[/math] (time terminated), let [math]\displaystyle{ {{M}_{q}}={{N}_{q}}\,\! }[/math]. Then:
- [math]\displaystyle{ M=\underset{q=1}{\overset{K}{\mathop \sum }}\,{{M}_{q}}\,\! }[/math]
Step 2: For each system, divide each successive failure time by the corresponding end time [math]\displaystyle{ {{T}_{q}}\,\! }[/math], [math]\displaystyle{ \,i=1,2,...,{{M}_{q}}.\,\! }[/math] Calculate the [math]\displaystyle{ M\,\! }[/math] values:
- [math]\displaystyle{ {{Y}_{iq}}=\frac{{{X}_{iq}}}{{{T}_{q}}},i=1,2,\ldots ,{{M}_{q}},\text{ }q=1,2,\ldots ,K\,\! }[/math]
Step 3: Next calculate [math]\displaystyle{ \bar{\beta }\,\! }[/math], the unbiased estimate of [math]\displaystyle{ \beta \,\! }[/math], from:
- [math]\displaystyle{ \bar{\beta }=\frac{M-1}{\underset{q=1}{\overset{K}{\mathop{\sum }}}\,\underset{i=1}{\overset{Mq}{\mathop{\sum }}}\,\ln \left( \tfrac{{{T}_{q}}}{{{X}_{i}}{{}_{q}}} \right)}\,\! }[/math]
Step 4: Treat the [math]\displaystyle{ {{Y}_{iq}}\,\! }[/math] values as one group, and order them from smallest to largest. Name these ordered values [math]\displaystyle{ {{z}_{1}},\,{{z}_{2}},\ldots ,{{z}_{M}}\,\! }[/math], such that [math]\displaystyle{ {{z}_{1}}\lt \ \ {{z}_{2}}\lt \ldots \lt {{z}_{M}}\,\! }[/math].
Step 5: Calculate the parametric Cramér-von Mises statistic.
- [math]\displaystyle{ C_{M}^{2}=\frac{1}{12M}+\underset{j=1}{\overset{M}{\mathop \sum }}\,{{(Z_{j}^{\overline{\beta }}-\frac{2j-1}{2M})}^{2}}\,\! }[/math]
Critical values for the Cramér-von Mises test are presented in the Crow-AMSAA (NHPP) page.
Step 6: If the calculated [math]\displaystyle{ C_{M}^{2}\,\! }[/math] is less than the critical value, then accept the hypothesis that the failure times for the [math]\displaystyle{ K\,\! }[/math] systems follow the non-homogeneous Poisson process with intensity function [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}}\,\! }[/math].
Chi-Squared Test
The parametric Cramér-von Mises test described above requires that the starting time, [math]\displaystyle{ {{S}_{q}}\,\! }[/math], be equal to 0 for each of the [math]\displaystyle{ K\,\! }[/math] systems. Although not as powerful as the Cramér-von Mises test, the chi-squared test can be applied regardless of the starting times. The expected number of failures for a system over its age [math]\displaystyle{ (a,b)\,\! }[/math] for the chi-squared test is estimated by [math]\displaystyle{ \widehat{\lambda }{{b}^{\widehat{\beta }}}-\widehat{\lambda }{{a}^{\widehat{\beta }}}=\widehat{\theta }\,\! }[/math], where [math]\displaystyle{ \widehat{\lambda }\,\! }[/math] and [math]\displaystyle{ \widehat{\beta }\,\! }[/math] are the maximum likelihood estimates.
The computed [math]\displaystyle{ {{\chi }^{2}}\,\! }[/math] statistic is:
- [math]\displaystyle{ {{\chi }^{2}}=\underset{j=1}{\overset{d}{\mathop \sum }}\,{{\frac{\left[ N(j)-\theta (j) \right]}{\widehat{\theta }(j)}}^{2}}\,\! }[/math]
where [math]\displaystyle{ d\,\! }[/math] is the total number of intervals. The random variable [math]\displaystyle{ {{\chi }^{2}}\,\! }[/math] is approximately chi-square distributed with [math]\displaystyle{ df=d-2\,\! }[/math] degrees of freedom. There must be at least three intervals and the length of the intervals do not have to be equal. It is common practice to require that the expected number of failures for each interval, [math]\displaystyle{ \theta (j)\,\! }[/math], be at least five. If [math]\displaystyle{ \chi _{0}^{2}\gt \chi _{\alpha /2,d-2}^{2}\,\! }[/math] or if [math]\displaystyle{ \chi _{0}^{2}\lt \chi _{1-(\alpha /2),d-2}^{2}\,\! }[/math], reject the null hypothesis.
Cramér-von Mises Example
For the data from power law model example given above, use the Cramér-von Mises test to examine the compatibility of the model at a significance level [math]\displaystyle{ \alpha =0.10\,\! }[/math]
Solution
Step 1:
- [math]\displaystyle{ \begin{align} {{X}_{9,1}}= & 1913.5\lt 2000,\,\ {{M}_{1}}=9 \\ {{X}_{11,2}}= & 1867\lt 2000,\,\ {{M}_{2}}=11 \\ {{X}_{14,3}}= & 1604.8\lt 2000,\,\ {{M}_{3}}=14 \\ M= & \underset{q=1}{\overset{3}{\mathop \sum }}\,{{M}_{q}}=34 \end{align}\,\! }[/math]
Step 2: Calculate [math]\displaystyle{ {{Y}_{iq}},\,\! }[/math] treat the [math]\displaystyle{ {{Y}_{iq}}\,\! }[/math] values as one group and order them from smallest to largest. Name these ordered values [math]\displaystyle{ {{z}_{1}},\,{{z}_{2}},\ldots ,{{z}_{M}}\,\! }[/math].
Step 3: Calculate:
- [math]\displaystyle{ \bar{\beta }=\tfrac{M-1}{\underset{q=1}{\overset{K}{\mathop{\sum }}}\,\underset{i=1}{\overset{Mq}{\mathop{\sum }}}\,\ln \left( \tfrac{{{T}_{q}}}{{{X}_{i}}{{}_{q}}} \right)}=0.4397\,\! }[/math]
Step 4: Calculate:
- [math]\displaystyle{ C_{M}^{2}=\tfrac{1}{12M}+\underset{j=1}{\overset{M}{\mathop{\sum }}}\,{{(Z_{j}^{\overline{\beta }}-\tfrac{2j-1}{2M})}^{2}}=0.0636\,\! }[/math]
Step 5: From the table of critical values for the Cramér-von Mises test, find the critical value (CV) for [math]\displaystyle{ M=34\,\! }[/math] at a significance level [math]\displaystyle{ \alpha =0.10\,\! }[/math]. [math]\displaystyle{ CV=0.172\,\! }[/math].
Step 6: Since [math]\displaystyle{ C_{M}^{2}\lt CV\,\! }[/math], accept the hypothesis that the failure times for the [math]\displaystyle{ K=3\,\! }[/math] repairable systems follow the non-homogeneous Poisson process with intensity function [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}}\,\! }[/math].
Confidence Bounds for Repairable Systems Analysis
The RGA software provides two methods to estimate the confidence bounds for repairable systems analysis. The Fisher matrix approach is based on the Fisher information matrix and is commonly employed in the reliability field. The Crow bounds were developed by Dr. Larry Crow. See Confidence Bounds for Repairable Systems Analysis for details on how these confidence bounds are calculated.
Confidence Bounds Example
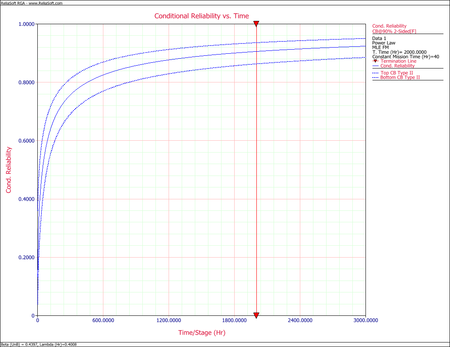
Using the data from the power law model example given above, calculate the mission reliability at [math]\displaystyle{ t=2000\,\! }[/math] hours and mission time [math]\displaystyle{ d=40\,\! }[/math] hours along with the confidence bounds at the 90% confidence level.
Solution
The maximum likelihood estimates of [math]\displaystyle{ \widehat{\lambda }\,\! }[/math] and [math]\displaystyle{ \widehat{\beta }\,\! }[/math] from the example are:
- [math]\displaystyle{ \begin{align} \widehat{\beta }= & 0.45300 \\ \widehat{\lambda }= & 0.36224 \end{align}\,\! }[/math]
The mission reliability at [math]\displaystyle{ t=2000\,\! }[/math] for mission time [math]\displaystyle{ d=40\,\! }[/math] is:
- [math]\displaystyle{ \begin{align} \widehat{R}(t)= & {{e}^{-\left[ \lambda {{\left( t+d \right)}^{\beta }}-\lambda {{t}^{\beta }} \right]}} \\ = & 0.90292 \end{align}\,\! }[/math]
At the 90% confidence level and [math]\displaystyle{ T=2000\,\! }[/math] hours, the Fisher matrix confidence bounds for the mission reliability for mission time [math]\displaystyle{ d=40\,\! }[/math] are given by:
- [math]\displaystyle{ CB=\frac{\widehat{R}(t)}{\widehat{R}(t)+(1-\widehat{R}(t)){{e}^{\pm {{z}_{\alpha }}\sqrt{Var(\widehat{R}(t))}/\left[ \widehat{R}(t)(1-\widehat{R}(t)) \right]}}}\,\! }[/math]
- [math]\displaystyle{ \begin{align} {{[\widehat{R}(t)]}_{L}}= & 0.83711 \\ {{[\widehat{R}(t)]}_{U}}= & 0.94392 \end{align}\,\! }[/math]
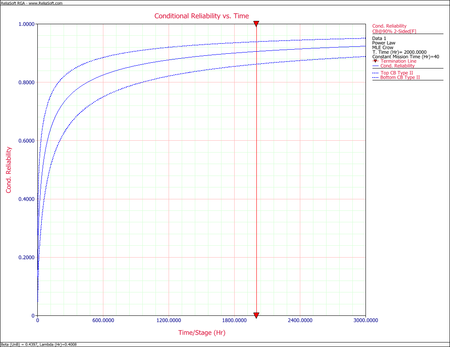
The Crow confidence bounds for the mission reliability are:
- [math]\displaystyle{ \begin{align} {{[\widehat{R}(t)]}_{L}}= & {{[\widehat{R}(\tau )]}^{\tfrac{1}{{{\Pi }_{1}}}}} \\ = & {{[0.90292]}^{\tfrac{1}{0.71440}}} \\ = & 0.86680 \\ {{[\widehat{R}(t)]}_{U}}= & {{[\widehat{R}(\tau )]}^{\tfrac{1}{{{\Pi }_{2}}}}} \\ = & {{[0.90292]}^{\tfrac{1}{1.6051}}} \\ = & 0.93836 \end{align}\,\! }[/math]
The next two figures show the Fisher matrix and Crow confidence bounds on mission reliability for mission time [math]\displaystyle{ d=40\,\! }[/math].
Economical Life Model
One consideration in reducing the cost to maintain repairable systems is to establish an overhaul policy that will minimize the total life cost of the system. However, an overhaul policy makes sense only if [math]\displaystyle{ \beta \gt 1\,\! }[/math]. It does not make sense to implement an overhaul policy if [math]\displaystyle{ \beta \lt 1\,\! }[/math] since wearout is not present. If you assume that there is a point at which it is cheaper to overhaul a system than to continue repairs, what is the overhaul time that will minimize the total life cycle cost while considering repair cost and the cost of overhaul?
Denote [math]\displaystyle{ {{C}_{1}}\,\! }[/math] as the average repair cost (unscheduled), [math]\displaystyle{ {{C}_{2}}\,\! }[/math] as the replacement or overhaul cost and [math]\displaystyle{ {{C}_{3}}\,\! }[/math] as the average cost of scheduled maintenance. Scheduled maintenance is performed for every [math]\displaystyle{ S\,\! }[/math] miles or time interval. In addition, let [math]\displaystyle{ {{N}_{1}}\,\! }[/math] be the number of failures in [math]\displaystyle{ [0,t]\,\! }[/math], and let [math]\displaystyle{ {{N}_{2}}\,\! }[/math] be the number of replacements in [math]\displaystyle{ [0,t]\,\! }[/math]. Suppose that replacement or overhaul occurs at times [math]\displaystyle{ T\,\! }[/math], [math]\displaystyle{ 2T\,\! }[/math], and [math]\displaystyle{ 3T\,\! }[/math]. The problem is to select the optimum overhaul time [math]\displaystyle{ T={{T}_{0}}\,\! }[/math] so as to minimize the long term average system cost (unscheduled maintenance, replacement cost and scheduled maintenance). Since [math]\displaystyle{ \beta \gt 1\,\! }[/math], the average system cost is minimized when the system is overhauled (or replaced) at time [math]\displaystyle{ {{T}_{0}}\,\! }[/math] such that the instantaneous maintenance cost equals the average system cost. The total system cost between overhaul or replacement is:
- [math]\displaystyle{ TSC(T)={{C}_{1}}E(N(T))+{{C}_{2}}+{{C}_{3}}\frac{T}{S}\,\! }[/math]
So the average system cost is:
- [math]\displaystyle{ C(T)=\frac{{{C}_{1}}E(N(T))+{{C}_{2}}+{{C}_{3}}\tfrac{T}{S}}{T}\,\! }[/math]
The instantaneous maintenance cost at time [math]\displaystyle{ T\,\! }[/math] is equal to:
- [math]\displaystyle{ IMC(T)={{C}_{1}}\lambda \beta {{T}^{\beta -1}}+\frac{{{C}_{3}}}{S}\,\! }[/math]
The following equation holds at optimum overhaul time [math]\displaystyle{ {{T}_{0}}\,\! }[/math] :
- [math]\displaystyle{ \begin{align} {{C}_{1}}\lambda \beta T_{0}^{\beta -1}+\frac{{{C}_{3}}}{S}= & \frac{{{C}_{1}}E(N(T))+{{C}_{2}}+{{C}_{3}}\tfrac{T}{S}}{T} \\ = & \frac{{{C}_{1}}\lambda T_{0}^{\beta }+{{C}_{2}}+{{C}_{3}}\tfrac{{{T}_{0}}}{S}}{{{T}_{0}}} \end{align}\,\! }[/math]
Therefore:
- [math]\displaystyle{ {{T}_{0}}={{\left[ \frac{{{C}_{2}}}{\lambda (\beta -1){{C}_{1}}} \right]}^{1/\beta }}\,\! }[/math]
But when there is no scheduled maintenance, the equation becomes:
- [math]\displaystyle{ {{C}_{1}}\lambda \beta T_{0}^{\beta -1}=\frac{{{C}_{1}}\lambda T_{0}^{\beta }+{{C}_{2}}}{{{T}_{0}}}\,\! }[/math]
and the equation for the optimum overhaul time, [math]\displaystyle{ {{T}_{0}}\,\! }[/math], is the same as in the previous case. Therefore, for periodic maintenance scheduled every [math]\displaystyle{ S\,\! }[/math] miles, the replacement or overhaul time is the same as for the unscheduled and replacement or overhaul cost model.
More Examples
Automatic Transmission Data Example
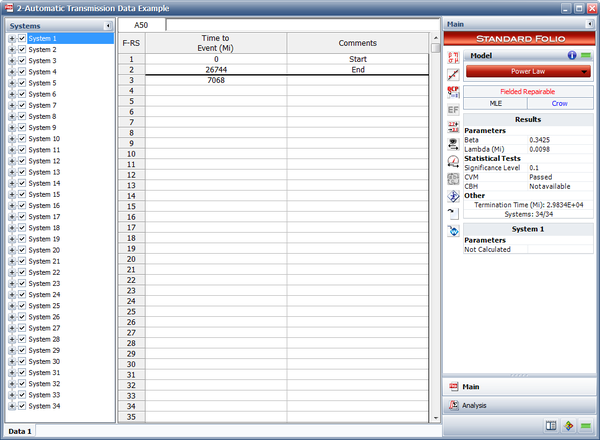
This case study is based on the data given in the article "Graphical Analysis of Repair Data" by Dr. Wayne Nelson [23]. The following table contains repair data on an automatic transmission from a sample of 34 cars. For each car, the data set shows mileage at the time of each transmission repair, along with the latest mileage. The + indicates the latest mileage observed without failure. Car 1, for example, had a repair at 7068 miles and was observed until 26,744 miles. Do the following:
- Estimate the parameters of the Power Law model.
- Estimate the number of warranty claims for a 36,000 mile warranty policy for an estimated fleet of 35,000 vehicles.
| Automatic Transmission Data | ||||
| Car | Mileage | Car | Mileage | |
|---|---|---|---|---|
| 1 | 7068, 26744+ | 18 | 17955+ | |
| 2 | 28, 13809+ | 19 | 19507+ | |
| 3 | 48, 1440, 29834+ | 20 | 24177+ | |
| 4 | 530, 25660+ | 21 | 22854+ | |
| 5 | 21762+ | 22 | 17844+ | |
| 6 | 14235+ | 23 | 22637+ | |
| 7 | 1388, 18228+ | 24 | 375, 19607+ | |
| 8 | 21401+ | 25 | 19403+ | |
| 9 | 21876+ | 26 | 20997+ | |
| 10 | 5094, 18228+ | 27 | 19175+ | |
| 11 | 21691+ | 28 | 20425+ | |
| 12 | 20890+ | 29 | 22149+ | |
| 13 | 22486+ | 30 | 21144+ | |
| 14 | 19321+ | 31 | 21237+ | |
| 15 | 21585+ | 32 | 14281+ | |
| 16 | 18676+ | 33 | 8250, 21974+ | |
| 17 | 23520+ | 34 | 19250, 21888+ | |
Solution
- The estimated Power Law parameters are shown next.
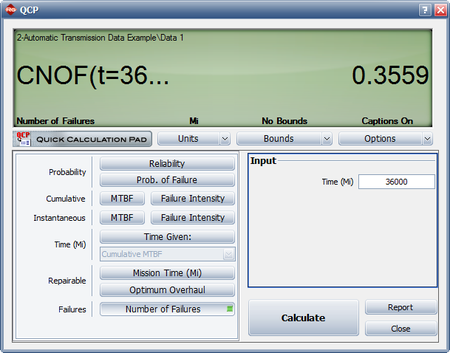
- The expected number of failures at 36,000 miles can be estimated using the QCP as shown next. The model predicts that 0.3559 failures per system will occur by 36,000 miles. This means that for a fleet of 35,000 vehicles, the expected warranty claims are 0.3559 * 35,000 = 12,456.
Optimum Overhaul Example
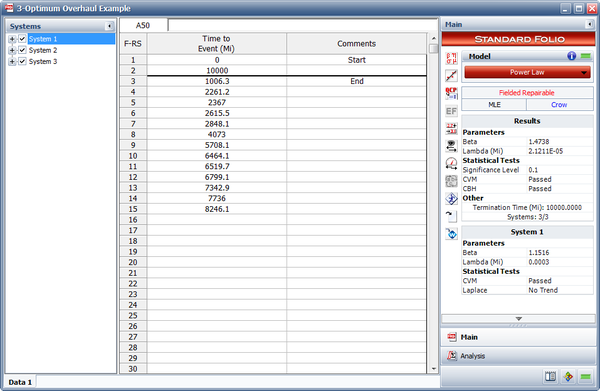
Field data have been collected for a system that begins its wearout phase at time zero. The start time for each system is equal to zero and the end time for each system is 10,000 miles. Each system is scheduled to undergo an overhaul after a certain number of miles. It has been determined that the cost of an overhaul is four times more expensive than a repair. The table below presents the data. Do the following:
- Estimate the parameters of the Power Law model.
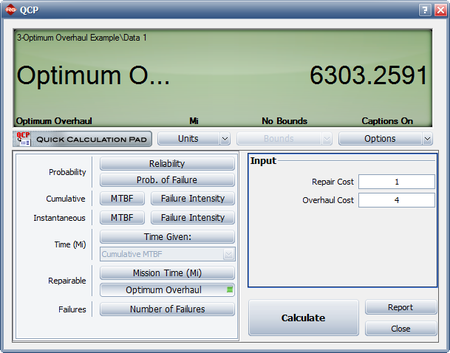
- Determine the optimum overhaul interval.
- If [math]\displaystyle{ \beta \lt 1\,\! }[/math], would it be cost-effective to implement an overhaul policy?
| Field Data | ||
| System 1 | System 2 | System 3 |
|---|---|---|
| 1006.3 | 722.7 | 619.1 |
| 2261.2 | 1950.9 | 1519.1 |
| 2367 | 3259.6 | 2956.6 |
| 2615.5 | 4733.9 | 3114.8 |
| 2848.1 | 5105.1 | 3657.9 |
| 4073 | 5624.1 | 4268.9 |
| 5708.1 | 5806.3 | 6690.2 |
| 6464.1 | 5855.6 | 6803.1 |
| 6519.7 | 6325.2 | 7323.9 |
| 6799.1 | 6999.4 | 7501.4 |
| 7342.9 | 7084.4 | 7641.2 |
| 7736 | 7105.9 | 7851.6 |
| 8246.1 | 7290.9 | 8147.6 |
| 7614.2 | 8221.9 | |
| 8332.1 | 9560.5 | |
| 8368.5 | 9575.4 | |
| 8947.9 | ||
| 9012.3 | ||
| 9135.9 | ||
| 9147.5 | ||
| 9601 | ||
Solution
- The next figure shows the estimated Power Law parameters.
- The QCP can be used to calculate the optimum overhaul interval, as shown next.
- Since [math]\displaystyle{ \beta \gt 1\,\! }[/math] the systems are wearing out and it would be cost-effective to implement an overhaul policy. An overhaul policy makes sense only if the systems are wearing out.
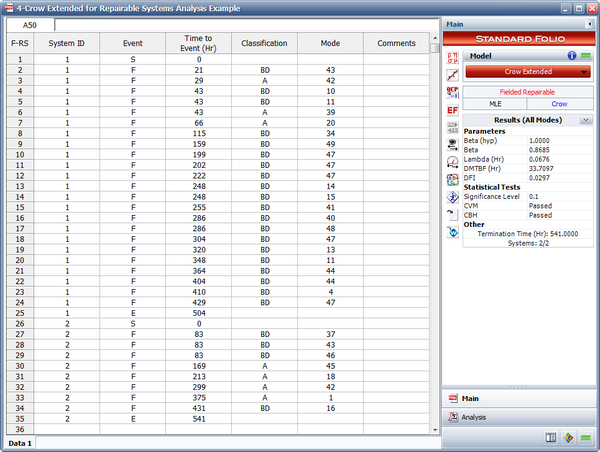
Crow Extended for Repairable Systems Analysis Example
The failures and fixes of two repairable systems in the field are recorded. Both systems started operating from time 0. System 1 ends at time = 504 and system 2 ends at time = 541. All the BD modes are fixed at the end of the test. A fixed effectiveness factor equal to 0.6 is used. Answer the following questions:
- Estimate the parameters of the Crow Extended model.
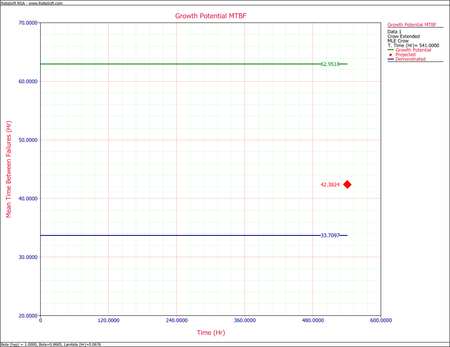
- Calculate the projected MTBF after the delayed fixes.
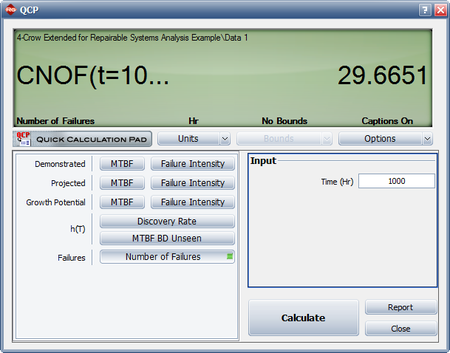
- If no fixes were performed for the future failures, what would be the expected number of failures at time 1,000?
Solution
- The next figure shows the estimated Crow Extended parameters.
- The next figure shows the projected MTBF at time = 541 (i.e., the age of the oldest system).
- The next figure shows the expected number of failures at time = 1,000.