Template:Example: Lognormal Distribution Likelihood Ratio Bound (Parameters)
Lognormal Distribution Likelihood Ratio Bound Example (Parameters)
Five units are put on a reliability test and experience failures at 45, 60, 75, 90, and 115 hours. Assuming a lognormal distribution, the MLE parameter estimates are calculated to be [math]\displaystyle{ {{\widehat{\mu }}^{\prime }}=4.2926 }[/math] and [math]\displaystyle{ {{\widehat{\sigma'}}}=0.32361. }[/math] Calculate the two-sided 75% confidence bounds on these parameters using the likelihood ratio method.
Solution
The first step is to calculate the likelihood function for the parameter estimates:
where [math]\displaystyle{ {{x}_{i}} }[/math] are the original time-to-failure data points. We can now rearrange the likelihod ratio equation to the form:
- [math]\displaystyle{ L({\mu }',{{\sigma' }})-L({{\widehat{\mu }}^{\prime }},{{\widehat{\sigma' }}})\cdot {{e}^{\tfrac{-\chi _{\alpha ;1}^{2}}{2}}}=0 }[/math]
Since our specified confidence level, [math]\displaystyle{ \delta }[/math] , is 75%, we can calculate the value of the chi-squared statistic, [math]\displaystyle{ \chi _{0.75;1}^{2}=1.323303. }[/math] We can now substitute this information into the equation:
- [math]\displaystyle{ \begin{align} & L({\mu }',{{\sigma' }})-L({{\widehat{\mu }}^{\prime }},{{\widehat{\sigma' }}})\cdot {{e}^{\tfrac{-\chi _{\alpha ;1}^{2}}{2}}}= & 0 \\ & L({\mu }',{{\sigma'}})-1.115256\times {{10}^{-10}}\cdot {{e}^{\tfrac{-1.323303}{2}}}= & 0 \\ & L({\mu }',{{\sigma'}})-5.754703\times {{10}^{-11}}= & 0 \end{align} }[/math]
It now remains to find the values of [math]\displaystyle{ {\mu }' }[/math] and [math]\displaystyle{ {{\sigma'}} }[/math] which satisfy this equation. This is an iterative process that requires setting the value of [math]\displaystyle{ {{\sigma'}} }[/math] and finding the appropriate values of [math]\displaystyle{ {\mu }' }[/math] , and vice versa.
The following table gives the values of [math]\displaystyle{ {\mu }' }[/math] based on given values of [math]\displaystyle{ {{\sigma'}} }[/math] .
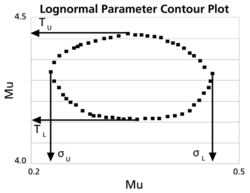
These points are represented graphically in the following contour plot:
(Note that this plot is generated with degrees of freedom [math]\displaystyle{ k=1 }[/math] , as we are only determining bounds on one parameter. The contour plots generated in Weibull++ are done with degrees of freedom [math]\displaystyle{ k=2 }[/math] , for use in comparing both parameters simultaneously.) As can be determined from the table the lowest calculated value for [math]\displaystyle{ {\mu }' }[/math] is 4.1145, while the highest is 4.4708. These represent the two-sided 75% confidence limits on this parameter. Since solutions for the equation do not exist for values of [math]\displaystyle{ {{\sigma' }} }[/math] below 0.24 or above 0.48, these can be considered the two-sided 75% confidence limits for this parameter. In order to obtain more accurate values for the confidence limits on [math]\displaystyle{ {{\sigma'}} }[/math] , we can perform the same procedure as before, but finding the two values of [math]\displaystyle{ \sigma }[/math] that correspond with a given value of [math]\displaystyle{ {\mu }'. }[/math] Using this method, we find that the 75% confidence limits on [math]\displaystyle{ {{\sigma'}} }[/math] are 0.23405 and 0.48936, which are close to the initial estimates of 0.24 and 0.48.