Template:Lognormal distribution bayesian confidence bounds

Bayesian Confidence Bounds

Bounds on Parameters

From Chapter 5, we know that the marginal distribution of parameter [math]\displaystyle{ {\mu }' }[/math] is:

[math]\displaystyle{ \begin{align} f({\mu }'|Data)= & \int_{0}^{\infty }f({\mu }',{{\sigma }_{{{T}'}}}|Data)d{{\sigma }_{{{T}'}}} \\ = & \frac{\int_{0}^{\infty }L(Data|{\mu }',{{\sigma }_{{{T}'}}})\varphi ({\mu }')\varphi ({{\sigma }_{{{T}'}}})d{{\sigma }_{{{T}'}}}}{\int_{0}^{\infty }\int_{-\infty }^{\infty }L(Data|{\mu }',{{\sigma }_{{{T}'}}})\varphi ({\mu }')\varphi ({{\sigma }_{{{T}'}}})d{\mu }'d{{\sigma }_{{{T}'}}}} \end{align} }[/math]

where:

[math]\displaystyle{ \varphi ({{\sigma }_{{{T}'}}}) }[/math] is [math]\displaystyle{ \tfrac{1}{{{\sigma }_{{{T}'}}}} }[/math] , non-informative prior of [math]\displaystyle{ {{\sigma }_{{{T}'}}} }[/math] .

[math]\displaystyle{ \varphi ({\mu }') }[/math] is an uniform distribution from - [math]\displaystyle{ \infty }[/math] to + [math]\displaystyle{ \infty }[/math] , non-informative prior of [math]\displaystyle{ {\mu }' }[/math] . With the above prior distributions, [math]\displaystyle{ f({\mu }'|Data) }[/math] can be rewritten as:

[math]\displaystyle{ f({\mu }'|Data)=\frac{\int_{0}^{\infty }L(Data|{\mu }',{{\sigma }_{{{T}'}}})\tfrac{1}{{{\sigma }_{{{T}'}}}}d{{\sigma }_{{{T}'}}}}{\int_{0}^{\infty }\int_{-\infty }^{\infty }L(Data|{\mu }',{{\sigma }_{{{T}'}}})\tfrac{1}{{{\sigma }_{{{T}'}}}}d{\mu }'d{{\sigma }_{{{T}'}}}} }[/math]

The one-sided upper bound of [math]\displaystyle{ {\mu }' }[/math] is:

[math]\displaystyle{ CL=P({\mu }'\le \mu _{U}^{\prime })=\int_{-\infty }^{\mu _{U}^{\prime }}f({\mu }'|Data)d{\mu }' }[/math]

The one-sided lower bound of [math]\displaystyle{ {\mu }' }[/math] is:

[math]\displaystyle{ 1-CL=P({\mu }'\le \mu _{L}^{\prime })=\int_{-\infty }^{\mu _{L}^{\prime }}f({\mu }'|Data)d{\mu }' }[/math]

The two-sided bounds of [math]\displaystyle{ {\mu }' }[/math] is:

[math]\displaystyle{ CL=P(\mu _{L}^{\prime }\le {\mu }'\le \mu _{U}^{\prime })=\int_{\mu _{L}^{\prime }}^{\mu _{U}^{\prime }}f({\mu }'|Data)d{\mu }' }[/math]

The same method can be used to obtained the bounds of [math]\displaystyle{ {{\sigma }_{{{T}'}}} }[/math] .

Bounds on Time (Type 1)

The reliable life of the lognormal distribution is:

[math]\displaystyle{ \ln T={\mu }'+{{\sigma }_{{{T}'}}}{{\Phi }^{-1}}(1-R) }[/math]

The one-sided upper on time bound is given by:

[math]\displaystyle{ CL=\underset{}{\overset{}{\mathop{\Pr }}}\,(\ln T\le \ln {{T}_{U}})=\underset{}{\overset{}{\mathop{\Pr }}}\,({\mu }'+{{\sigma }_{{{T}'}}}{{\Phi }^{-1}}(1-R)\le \ln {{T}_{U}}) }[/math]

Eqn. (1SBT) can be rewritten in terms of [math]\displaystyle{ {\mu }' }[/math] as:

[math]\displaystyle{ CL=\underset{}{\overset{}{\mathop{\Pr }}}\,({\mu }'\le \ln {{T}_{U}}-{{\sigma }_{{{T}'}}}{{\Phi }^{-1}}(1-R) }[/math]

From the posterior distribution of [math]\displaystyle{ {\mu }' }[/math] get:

[math]\displaystyle{ CL=\frac{\int_{0}^{\infty }\int_{-\infty }^{\ln {{T}_{U}}-{{\sigma }_{{{T}'}}}{{\Phi }^{-1}}(1-R)}L({{\sigma }_{{{T}'}}},{\mu }')\tfrac{1}{{{\sigma }_{{{T}'}}}}d{\mu }'d{{\sigma }_{{{T}'}}}}{\int_{0}^{\infty }\int_{-\infty }^{\infty }L({{\sigma }_{{{T}'}}},{\mu }')\tfrac{1}{{{\sigma }_{{{T}'}}}}d{\mu }'d{{\sigma }_{{{T}'}}}} }[/math]

Eqn. (1SCBT) is solved w.r.t. [math]\displaystyle{ {{T}_{U}}. }[/math] The same method can be applied for one-sided lower bounds and two-sided bounds on Time.

Bounds on Reliability (Type 2)

The one-sided upper bound on reliability is given by:

[math]\displaystyle{ CL=\underset{}{\overset{}{\mathop{\Pr }}}\,(R\le {{R}_{U}})=\underset{}{\overset{}{\mathop{\Pr }}}\,({\mu }'\le \ln T-{{\sigma }_{{{T}'}}}{{\Phi }^{-1}}(1-{{R}_{U}})) }[/math]

From the posterior distribution of [math]\displaystyle{ {\mu }' }[/math] is:

[math]\displaystyle{ CL=\frac{\int_{0}^{\infty }\int_{-\infty }^{\ln T-{{\sigma }_{{{T}'}}}{{\Phi }^{-1}}(1-{{R}_{U}})}L({{\sigma }_{{{T}'}}},{\mu }')\tfrac{1}{{{\sigma }_{{{T}'}}}}d{\mu }'d{{\sigma }_{{{T}'}}}}{\int_{0}^{\infty }\int_{-\infty }^{\infty }L({{\sigma }_{{{T}'}}},{\mu }')\tfrac{1}{{{\sigma }_{{{T}'}}}}d{\mu }'d{{\sigma }_{{{T}'}}}} }[/math]

Eqn. (1SCBR) is solved w.r.t. [math]\displaystyle{ {{R}_{U}}. }[/math] The same method is used to calculate the one-sided lower bounds and two-sided bounds on Reliability.

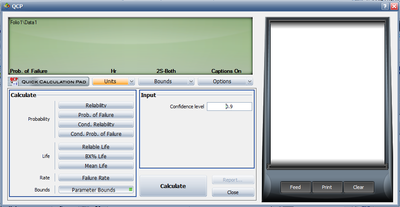
Example 8

Determine the two-sided 90% Bayesian confidence bounds on the lognormal parameter estimates for the data given next:

[math]\displaystyle{ \begin{matrix} \text{Data Point Index} & \text{State End Time} \\ \text{1} & \text{2} \\ \text{2} & \text{5} \\ \text{3} & \text{11} \\ \text{4} & \text{23} \\ \text{5} & \text{29} \\ \text{6} & \text{37} \\ \text{7} & \text{43} \\ \text{8} & \text{59} \\ \end{matrix} }[/math]

Solution to Example 8

The data is entered into a Times-to-failure data sheet. The lognormal distribution is selected under Distributions. The Bayesian confidence bounds method only applies for the MLE analysis method, therefore, Maximum Likelihood (MLE) is selected under Analysis Method and Use Bayesian is selected under the Confidence Bounds Method in the Analysis tab.

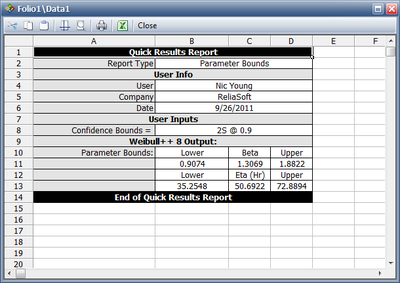
The two-sided 90% Bayesian confidence bounds on the lognormal parameter are obtained using the QCP and clicking on the Calculate Bounds button in the Parameter Bounds tab as follows:

[math]\displaystyle{ }[/math]