The Loglogistic Distribution: Difference between revisions

From ReliaWiki
Jump to navigation Jump to search
No edit summary
 
(47 intermediate revisions by 7 users not shown)
Line 1: Line 1:
{{template:LDABOOK|15|The LogLogistic Distribution}}
{{template:LDABOOK|15|The LogLogistic Distribution}}
As may be indicated by the name, the loglogistic distribution has certain similarities to the logistic distribution. A random variable is loglogistically distributed if the logarithm of the random variable is logistically distributed. Because of this, there are many mathematical similarities between the two distributions, as discussed in Meeker and Escobar [[Appendix:_Life_Data_Analysis_References|[27]]]. For example, the mathematical reasoning for the construction of the probability plotting scales is very similar for these two distributions.


===The Loglogistic Distribution===
===Loglogistic Probability Density Function===
As may be indicated by the name, the loglogistic distribution has certain similarities to the logistic distribution. A random variable is loglogistically distributed if the logarithm of the random variable is logistically distributed. Because of this, there are many mathematical similarities between the two distributions [27]. For example, the mathematical reasoning for the construction of the probability plotting scales is very similar for these two distributions.
The loglogistic distribution is a 2-parameter distribution with parameters <math>\mu \,\!</math> and <math>\sigma \,\!</math>. The ''pdf'' for this distribution is given by:


====Loglogistic Probability Density Function====
::<math>f(t)=\frac{{{e}^{z}}}{\sigma {t}{{(1+{{e}^{z}})}^{2}}}\,\!</math>
The loglogistic distribution is a two-parameter distribution with parameters  <math>\mu </math>  and  <math>\sigma </math> . The  <math>pdf</math>  for this distribution is given by:  
 
<math>f(T)=\frac{{{e}^{z}}}{\sigma T{{(1+{{e}^{z}})}^{2}}}</math>


where:  
where:  


<math>z=\frac{{T}'-\mu }{\sigma }</math>
::<math>z=\frac{{t}'-\mu }{\sigma }\,\!</math>


<math>{T}'=\ln (T)</math>
::<math>{t}'=\ln (t)\,\!</math>


and:  
and:  


<math>\begin{align}
::<math>\begin{align}
   & \mu = & \text{scale parameter} \\  
   & \mu = & \text{scale parameter} \\  
  & \sigma = & \text{shape parameter}   
  & \sigma = & \text{shape parameter}   
\end{align}</math>
\end{align}\,\!</math>
 
where  <math>0<t<\infty </math> ,  <math>-\infty <\mu <\infty </math>  and  <math>0<\sigma <\infty </math> .
 
====Mean, Median and Mode====
The mean of the loglogistic distribution, <math>\overline{T}</math> , is given by:


<math>\overline{T}={{e}^{\mu }}\Gamma (1+\sigma )\Gamma (1-\sigma )</math>
where <math>0<t<\infty \,\!</math>, <math>-\infty <\mu <\infty \,\!</math> and <math>0<\sigma <\infty \,\!</math>.


===Mean, Median and Mode===
The mean of the loglogistic distribution, <math>\overline{T}\,\!</math>, is given by:


Note that for  <math>\sigma \ge 1,</math>  <math>\overline{T}</math> does not exist.
::<math>\overline{T}={{e}^{\mu }}\Gamma (1+\sigma )\Gamma (1-\sigma )\,\!</math>


The median of the loglogistic distribution, <math>\breve{T}</math> , is given by:
Note that for <math>\sigma \ge 1,\,\!</math> <math>\overline{T}\,\!</math> does not exist.


<math>\widehat{T}={{e}^{\mu }}</math>
The median of the loglogistic distribution, <math>\breve{T}\,\!</math>, is given by:


The mode of the loglogistic distribution,  <math>\tilde{T}</math> , if  <math>\sigma <1,</math> is given by:
::<math>\widehat{T}={{e}^{\mu }}\,\!</math>


..
The mode of the loglogistic distribution, <math>\tilde{T}\,\!</math>, if <math>\sigma <1,\,\!</math> is given by:


====The Standard Deviation====
::<math>\tilde{T} = e^{\mu+\sigma ln(\frac{1-\sigma}{1+\sigma})}\,\!</math>
The standard deviation of the loglogistic distribution,  <math>{{\sigma }_{T}}</math> , is given by:


<math>{{\sigma }_{T}}={{e}^{\mu }}\sqrt{\Gamma (1+2\sigma )\Gamma (1-2\sigma )-{{(\Gamma (1+\sigma )\Gamma (1-\sigma ))}^{2}}}</math>
===The Standard Deviation===
The standard deviation of the loglogistic distribution, <math>{{\sigma }_{T}}\,\!</math>, is given by:


::<math>{{\sigma }_{T}}={{e}^{\mu }}\sqrt{\Gamma (1+2\sigma )\Gamma (1-2\sigma )-{{(\Gamma (1+\sigma )\Gamma (1-\sigma ))}^{2}}}\,\!</math>


Note that for <math>\sigma \ge 0.5,</math> the standard deviation does not exist.
Note that for <math>\sigma \ge 0.5,\,\!</math> the standard deviation does not exist.


====The Loglogistic Reliability Function====
===The Loglogistic Reliability Function===
The reliability for a mission of time <math>T</math> , starting at age 0, for the loglogistic distribution is determined by:
The reliability for a mission of time <math>T\,\!</math>, starting at age 0, for the loglogistic distribution is determined by:


<math>R=\frac{1}{1+{{e}^{z}}}</math>
::<math>R=\frac{1}{1+{{e}^{z}}}\,\!</math>


where:
where:


<math>z=\frac{{T}'-\mu }{\sigma }</math>
::<math>z=\frac{{t}'-\mu }{\sigma }\,\!</math>


::<math>\begin{align}
<math>{T}'=\ln (t)</math>
{t}'=\ln (t)
\end{align}\,\!</math>


The unreliability function is:
The unreliability function is:


<math>F=\frac{{{e}^{z}}}{1+{{e}^{z}}}</math>
::<math>F=\frac{{{e}^{z}}}{1+{{e}^{z}}}\,\!</math>


====The loglogistic Reliable Life====
===The loglogistic Reliable Life===
The  logistic reliable life is:
The  logistic reliable life is:


::<math>\begin{align}
{{T}_{R}}={{e}^{\mu +\sigma [\ln (1-R)-\ln (R)]}}
\end{align}\,\!</math>


<math>{{T}_{R}}={{e}^{\mu +\sigma [\ln (1-R)-\ln (R)]}}</math>
===The loglogistic Failure Rate Function===
 
====The loglogistic Failure Rate Function====
The loglogistic failure rate is given by:
The loglogistic failure rate is given by:


::<math>\lambda (t)=\frac{{{e}^{z}}}{\sigma t(1+{{e}^{z}})}\,\!</math>


<math>\lambda (T)=\frac{{{e}^{z}}}{\sigma T(1+{{e}^{z}})}</math>
==Distribution Characteristics==
 
For <math>\sigma >1\,\!</math> :
 
====Distribution Characteristics====
For <math>\sigma >1</math> :
 
• <math>f(T)</math>  decreases monotonically and is convex. Mode and mean do not exist.
 
For  <math>\sigma =1</math> :
 
• <math>f(T)</math>  decreases monotonically and is convex. Mode and mean do not exist. As  <math>T\to 0</math> ,  <math>f(T)\to \tfrac{1}{\sigma {{e}^{\tfrac{\mu }{\sigma }}}}.</math>
 
• As  <math>T\to 0</math>  , <math>\lambda (T)\to \tfrac{1}{\sigma {{e}^{\tfrac{\mu }{\sigma }}}}.</math>
 
For  <math>0<\sigma <1</math> :
 
• The shape of the loglogistic distribution is very similar to that of the lognormal distribution and the Weibull distribution.


• The <math>pdf</math> starts at zero, increases to its mode, and decreases thereafter.
:* <math>f(t)\,\!</math> decreases monotonically and is convex. Mode and mean do not exist.


• As  <math>\mu </math>  increases, while  <math>\sigma </math> is kept the same, the  <math>pdf</math>  gets stretched out to the right and its height decreases, while maintaining its shape.
For <math>\sigma =1\,\!</math> :


• As <math>\mu </math> decreases,while  <math>\sigma </math> is kept the same, the  ..  gets pushed in towards the left and its height increases.
:* <math>f(t)\,\!</math> decreases monotonically and is convex. Mode and mean do not exist. As <math>t\to 0\,\!</math>, <math>f(t)\to \tfrac{1}{\sigma {{e}^{\tfrac{\mu }{\sigma }}}}.\,\!</math>
:* As <math>t\to 0\,\!</math>, <math>\lambda (t)\to \tfrac{1}{\sigma {{e}^{\tfrac{\mu }{\sigma }}}}.\,\!</math>


• <math>\lambda (T)</math>  increases till  <math>T={{e}^{\mu +\sigma \ln (\tfrac{1-\sigma }{\sigma })}}</math>   and decreases thereafter.  <math>\lambda (T)</math>  is concave at first, then becomes convex.
For <math>0<\sigma <1\,\!</math> :


====Confidence Bounds====
:* The shape of the loglogistic distribution is very similar to that of the lognormal distribution and the Weibull distribution.
The method used by the application in estimating the different types of confidence bounds for loglogistically distributed data is presented in this section. The complete derivations were presented in detail for a general function in Chapter 5.
:* The ''pdf''  starts at zero, increases to its mode, and decreases thereafter.
====Bounds on the Parameters====
:* As <math>\mu \,\!</math> increases, while <math>\sigma \,\!</math> is kept the same, the ''pdf'' gets stretched out to the right and its height decreases, while maintaining its shape.
The lower and upper bounds on the mean,  <math>{\mu }'</math> , are estimated from:
:* As <math>\mu \,\!</math> decreases,while <math>\sigma \,\!</math> is kept the same, the  ''pdf'' gets pushed in towards the left and its height increases.
:* <math>\lambda (t)\,\!</math> increases till <math>t={{e}^{\mu +\sigma \ln (\tfrac{1-\sigma }{\sigma })}}\,\!</math>  and decreases thereafter. <math>\lambda (t)\,\!</math> is concave at first, then becomes convex.


[[Image:WB.15 loglogistic pdf.png|center|400px| ]]


<math>\begin{align}
==Confidence Bounds==
  & \mu _{U}^{\prime }= & {{\widehat{\mu }}^{\prime }}+{{K}_{\alpha }}\sqrt{Var(\widehat{\mu })}\text{ (upper bound)} \\
The method used by the application in estimating the different types of confidence bounds for loglogistically distributed data is presented in this section. The complete derivations were presented in detail for a general function in [[Parameter Estimation]].
& \mu _{L}^{\prime }= & {{\widehat{\mu }}^{\prime }}-{{K}_{\alpha }}\sqrt{Var(\widehat{\mu })}\text{ (lower bound)} 
\end{align}</math>


===Bounds on the Parameters===
The lower and upper bounds <math>{\mu }\,\!</math>, are estimated from:


For the standard deviation,  <math>{{\widehat{\sigma }}_{{{T}'}}}</math> , <math>\ln ({{\widehat{\sigma }}_{{{T}'}}})</math> is treated as normally distributed, and the bounds are estimated from:
::<math>\begin{align}
  & \mu _{U}= & {{\widehat{\mu }}}+{{K}_{\alpha }}\sqrt{Var(\widehat{\mu })}\text{ (upper bound)} \\
  & \mu _{L}= & {{\widehat{\mu }}}-{{K}_{\alpha }}\sqrt{Var(\widehat{\mu })}\text{ (lower bound)}
\end{align}\,\!</math>


<math>\begin{align}
For paramter <math>{{\widehat{\sigma }}}\,\!</math>, <math>\ln ({{\widehat{\sigma }}})\,\!</math> is treated as normally distributed, and the bounds are estimated from:
  & {{\sigma }_{U}}= & {{\widehat{\sigma }}_{{{T}'}}}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{\sigma })}}{\widehat{\sigma }}}}\text{ (upper bound)} \\
& {{\sigma }_{L}}= & \frac{{{\widehat{\sigma }}_{{{T}'}}}}{{{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{\sigma })}}{{{\widehat{\sigma }}_{{{T}'}}}}}}}\text{ (lower bound)} 
\end{align}</math>


where  <math>{{K}_{\alpha }}</math> is defined by:
::<math>\begin{align}
  & {{\sigma }_{U}}= & {{\widehat{\sigma }}}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{\sigma })}}{\widehat{\sigma }}}}\text{ (upper bound)} \\
& {{\sigma }_{L}}= & \frac{{{\widehat{\sigma }}}}{{{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{\sigma })}}{{{\widehat{\sigma }}}}}}}\text{ (lower bound)} 
\end{align}\,\!</math>


<math>\alpha =\frac{1}{\sqrt{2\pi }}\int_{{{K}_{\alpha }}}^{\infty }{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt=1-\Phi ({{K}_{\alpha }})</math>
where <math>{{K}_{\alpha }}\,\!</math> is defined by:


::<math>\alpha =\frac{1}{\sqrt{2\pi }}\int_{{{K}_{\alpha }}}^{\infty }{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt=1-\Phi ({{K}_{\alpha }})\,\!</math>


If <math>\delta </math> is the confidence level, then <math>\alpha =\tfrac{1-\delta }{2}</math> for the two-sided bounds, and <math>\alpha =1-\delta </math> for the one-sided bounds.
If <math>\delta \,\!</math> is the confidence level, then <math>\alpha =\tfrac{1-\delta }{2}\,\!</math> for the two-sided bounds, and <math>\alpha =1-\delta \,\!</math> for the one-sided bounds.


The variances and covariances of <math>\widehat{\mu }</math> and <math>\widehat{\sigma }</math> are estimated as follows:  
The variances and covariances of <math>\widehat{\mu }\,\!</math> and <math>\widehat{\sigma }\,\!</math> are estimated as follows:  


<math>\left( \begin{matrix}
::<math>\left( \begin{matrix}
   \widehat{Var}\left( \widehat{\mu } \right) & \widehat{Cov}\left( \widehat{\mu },\widehat{\sigma } \right)  \\
   \widehat{Var}\left( \widehat{\mu } \right) & \widehat{Cov}\left( \widehat{\mu },\widehat{\sigma } \right)  \\
   \widehat{Cov}\left( \widehat{\mu },\widehat{\sigma } \right) & \widehat{Var}\left( \widehat{\sigma } \right)  \\
   \widehat{Cov}\left( \widehat{\mu },\widehat{\sigma } \right) & \widehat{Var}\left( \widehat{\sigma } \right)  \\
Line 135: Line 126:
   {} & {}  \\
   {} & {}  \\
   -\tfrac{{{\partial }^{2}}\Lambda }{\partial \mu \partial \sigma } & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\sigma }^{2}}}  \\
   -\tfrac{{{\partial }^{2}}\Lambda }{\partial \mu \partial \sigma } & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\sigma }^{2}}}  \\
\end{matrix} \right)_{\mu =\widehat{\mu },\sigma =\widehat{\sigma }}^{-1}</math>
\end{matrix} \right)_{\mu =\widehat{\mu },\sigma =\widehat{\sigma }}^{-1}\,\!</math>


where <math>\Lambda \,\!</math> is the log-likelihood function of the loglogistic distribution.


where  <math>\Lambda </math>  is the log-likelihood function of the loglogistic distribution.
===Bounds on Reliability===
 
====Bounds on Reliability====
The reliability of the logistic distribution is:  
The reliability of the logistic distribution is:  


<math>\widehat{R}=\frac{1}{1+\exp (\widehat{z})}</math>
::<math>\widehat{R}=\frac{1}{1+\exp (\widehat{z})}\,\!</math>
 


where:  
where:  


<math>\widehat{z}=\frac{{T}'-\widehat{\mu }}{\widehat{\sigma }}</math>
::<math>\widehat{z}=\frac{{t}'-\widehat{\mu }}{\widehat{\sigma }}\,\!</math>
 


Here <math>0<t<\infty </math> , <math>-\infty <\mu <\infty </math> , <math>0<\sigma <\infty </math> , therefore <math>0<\ln (t)<\infty </math>     and <math>z</math> also is changing from <math>-\infty </math> till <math>+\infty </math> .The bounds on  <math>z</math>  are estimated from:
Here <math>0<t<\infty \,\!</math>, <math>-\infty <\mu <\infty \,\!</math>, <math>0<\sigma <\infty \,\!</math>, therefore <math>0<t'=\ln (t)<\infty \,\!</math>   and <math>z\,\!</math> also is changing from <math>-\infty \,\!</math> till <math>+\infty \,\!</math>.


<math>{{z}_{U}}=\widehat{z}+{{K}_{\alpha }}\sqrt{Var(\widehat{z})}</math>
The bounds on <math>z\,\!</math> are estimated from:


::<math>{{z}_{U}}=\widehat{z}+{{K}_{\alpha }}\sqrt{Var(\widehat{z})}\,\!</math>
 
<math>{{z}_{L}}=\widehat{z}-{{K}_{\alpha }}\sqrt{Var(\widehat{z})\text{ }}\text{ }</math>


::<math>{{z}_{L}}=\widehat{z}-{{K}_{\alpha }}\sqrt{Var(\widehat{z})\text{ }}\text{ }\,\!</math>


where:  
where:  


<math>Var(\widehat{z})={{(\frac{\partial z}{\partial \mu })}^{2}}Var({{\widehat{\mu }}^{\prime }})+2(\frac{\partial z}{\partial \mu })(\frac{\partial z}{\partial \sigma })Cov(\widehat{\mu },\widehat{\sigma })+{{(\frac{\partial z}{\partial \sigma })}^{2}}Var(\widehat{\sigma })</math>
::<math>Var(\widehat{z})={{(\frac{\partial z}{\partial \mu })}^{2}}Var({{\widehat{\mu }}^{\prime }})+2(\frac{\partial z}{\partial \mu })(\frac{\partial z}{\partial \sigma })Cov(\widehat{\mu },\widehat{\sigma })+{{(\frac{\partial z}{\partial \sigma })}^{2}}Var(\widehat{\sigma })\,\!</math>
 


or:  
or:  


<math>Var(\widehat{z})=\frac{1}{{{\sigma }^{2}}}(Var(\widehat{\mu })+2\widehat{z}Cov(\widehat{\mu },\widehat{\sigma })+{{\widehat{z}}^{2}}Var(\widehat{\sigma }))</math>
::<math>Var(\widehat{z})=\frac{1}{{{\sigma }^{2}}}(Var(\widehat{\mu })+2\widehat{z}Cov(\widehat{\mu },\widehat{\sigma })+{{\widehat{z}}^{2}}Var(\widehat{\sigma }))\,\!</math>
 


The upper and lower bounds on reliability are:  
The upper and lower bounds on reliability are:  


<math>{{R}_{U}}=\frac{1}{1+{{e}^{{{z}_{L}}}}}\text{(Upper bound)}</math>
::<math>{{R}_{U}}=\frac{1}{1+{{e}^{{{z}_{L}}}}}\text{(Upper bound)}\,\!</math>


::<math>{{R}_{L}}=\frac{1}{1+{{e}^{{{z}_{U}}}}}\text{(Lower bound)}\,\!</math>


<math>{{R}_{L}}=\frac{1}{1+{{e}^{{{z}_{U}}}}}\text{(Lower bound)}</math>
===Bounds on Time===
 
 
====Bounds on Time====
The bounds around time for a given loglogistic percentile, or unreliability, are estimated by first solving the reliability equation with respect to time, as follows:  
The bounds around time for a given loglogistic percentile, or unreliability, are estimated by first solving the reliability equation with respect to time, as follows:  


<math>\widehat{T}(\widehat{\mu },\widehat{\sigma })={{e}^{\widehat{\mu }+\widehat{\sigma }z}}</math>
::<math>\widehat{T}(\widehat{\mu },\widehat{\sigma })={{e}^{\widehat{\mu }+\widehat{\sigma }z}}\,\!</math>
 


where:  
where:  


<math>z=\ln (1-R)-\ln (R)</math>
::<math>\begin{align}
 
z=\ln (1-R)-\ln (R)
\end{align}\,\!</math>


or:  
or:  


<math>\ln (T)=\widehat{\mu }+\widehat{\sigma }z</math>
::<math>\ln (\hat{T})=\widehat{\mu }+\widehat{\sigma }z\,\!</math>
 


Let:  
Let:  


<math>u=\ln (T)=\widehat{\mu }+\widehat{\sigma }z</math>
::<math>{u}=\ln (\hat{T})=\widehat{\mu }+\widehat{\sigma }z\,\!</math>
 


then:  
then:  


<math>{{u}_{U}}=\widehat{u}+{{K}_{\alpha }}\sqrt{Var(\widehat{u})\text{ }}\text{ }</math>
::<math>{u}_{U}=\widehat{u}+{{K}_{\alpha }}\sqrt{Var(\widehat{u})\text{ }}\text{ }\,\!</math>
 
 




<math>{{u}_{L}}=\widehat{u}-{{K}_{\alpha }}\sqrt{Var(\widehat{u})\text{ }}\text{ }</math>
::<math>{u}_{L}=\widehat{u}-{{K}_{\alpha }}\sqrt{Var(\widehat{u})\text{ }}\text{ }\,\!</math>
 


where:
where:


 
::<math>Var(\widehat{u})={{(\frac{\partial u}{\partial \mu })}^{2}}Var(\widehat{\mu })+2(\frac{\partial u}{\partial \mu })(\frac{\partial u}{\partial \sigma })Cov(\widehat{\mu },\widehat{\sigma })+{{(\frac{\partial u}{\partial \sigma })}^{2}}Var(\widehat{\sigma })\,\!</math>
<math>Var(\widehat{u})={{(\frac{\partial u}{\partial \mu })}^{2}}Var(\widehat{\mu })+2(\frac{\partial u}{\partial \mu })(\frac{\partial u}{\partial \sigma })Cov(\widehat{\mu },\widehat{\sigma })+{{(\frac{\partial u}{\partial \sigma })}^{2}}Var(\widehat{\sigma })</math>
 


or:  
or:  


<math>Var(\widehat{u})=Var(\widehat{\mu })+2\widehat{z}Cov(\widehat{\mu },\widehat{\sigma })+{{\widehat{z}}^{2}}Var(\widehat{\sigma })</math>
::<math>Var(\widehat{u})=Var(\widehat{\mu })+2\widehat{z}Cov(\widehat{\mu },\widehat{\sigma })+{{\widehat{z}}^{2}}Var(\widehat{\sigma })\,\!</math>
 


The upper and lower bounds are then found by:  
The upper and lower bounds are then found by:  


<math>{{T}_{U}}={{e}^{{{u}_{U}}}}\text{ (upper bound)}</math>
::<math>{{T}_{U}}={{e}^{{{u}_{U}}}}\text{ (upper bound)}\,\!</math>
 
 
<math>{{T}_{L}}={{e}^{{{u}_{L}}}}\text{ (lower bound)}</math>
 
 
====A LogLogistic Distribution Example====
Determine the loglogistic parameter estimates for the data given in Table 10.3.
 
<math>\overset{{}}{\mathop{\text{Table 10}\text{.3 - Test data}}}\,</math>
 
 
<math>\begin{matrix}
  \text{Data point index} & \text{Last Inspected} & \text{State End time}  \\
  \text{1} & \text{105} & \text{106}  \\
  \text{2} & \text{197} & \text{200}  \\
  \text{3} & \text{297} & \text{301}  \\
  \text{4} & \text{330} & \text{335}  \\
  \text{5} & \text{393} & \text{401}  \\
  \text{6} & \text{423} & \text{426}  \\
  \text{7} & \text{460} & \text{468}  \\
  \text{8} & \text{569} & \text{570}  \\
  \text{9} & \text{675} & \text{680}  \\
  \text{10} & \text{884} & \text{889}  \\
\end{matrix}</math>
 
 
Using Times-to-failure data under the Folio Data Type and the My data set contains interval and/or left censored data under Times-to-failure data options to enter the above data, the computed parameters for maximum likelihood are calculated to be:
 
<math>\begin{align}
  & {{{\hat{\mu }}}^{\prime }}= & 5.9772 \\
& {{{\hat{\sigma }}}_{{{T}'}}}= & 0.3256 
\end{align}</math>
 
 
For rank regression on  <math>X\ \ :</math> 
 
<math>\begin{align}
  & \hat{\mu }= & 5.9281 \\
& \hat{\sigma }= & 0.3821 
\end{align}</math>
 
 
For rank regression on  <math>Y\ \ :</math> 
 
<math>\begin{align}
  & \hat{\mu }= & 5.9772 \\
& \hat{\sigma }= & 0.3256 
\end{align}</math>
 
===The Gumbel/SEV Distribution===
The Gumbel distribution is also referred to as the Smallest Extreme Value (SEV) distribution or the Smallest Extreme Value (Type I) distribution. The Gumbel distribution's  <math>pdf</math>  is skewed to the left, unlike the Weibull distribution's  <math>pdf</math> , which is skewed to the right. The Gumbel distribution is appropriate for modeling strength, which is sometimes skewed to the left (few weak units in the lower tail, most units in the upper tail of the strength population). The Gumbel distribution could also be appropriate for modeling the life of products that experience very quick wear-out after reaching a certain age. The distribution of logarithms of times can often be modeled with the Gumbel distribution (in addition to the more common lognormal distribution). [27]
====Gumbel Probability Density Function====
The  <math>pdf</math>  of the Gumbel distribution is given by:  
 
<math>f(T)=\frac{1}{\sigma }{{e}^{z-{{e}^{z}}}}</math>
 
 
 
<math>f(T)\ge 0,\sigma >0</math>
where:
 
<math>z=\frac{T-\mu }{\sigma }</math>
 
and:
 
<math>\begin{align}
  & \mu = & \text{location parameter} \\
& \sigma = & \text{scale parameter} 
\end{align}</math>
 
 
====The Gumbel Mean, Median and Mode====
The Gumbel mean or MTTF is:
 
<math>\overline{T}=\mu -\sigma \gamma </math>
 
where  <math>\gamma \approx 0.5772</math>  (Euler's constant).
 
The mode of the Gumbel distribution is:
 
<math>\tilde{T}=\mu </math>
 
The median of the Gumbel distribution is:
 
<math>\widehat{T}=\mu +\sigma \ln (\ln (2))</math>
 
====The Gumbel Standard Deviation====
The standard deviation for the Gumbel distribution is given by:
 
<math>{{\sigma }_{T}}=\sigma \pi \frac{\sqrt{6}}{6}</math>
 
 
====The Gumbel Reliability Function====
The reliability for a mission of time  <math>T</math>  for the Gumbel distribution is given by:
 
<math>R(T)={{e}^{-{{e}^{z}}}}</math>
 
The unreliability function is given by:
 
<math>F(T)=1-{{e}^{-{{e}^{z}}}}</math>
 
====The Gumbel Reliable Life====
The Gumbel reliable life is given by:
 
 
<math>{{T}_{R}}=\mu +\sigma [\ln (-\ln (R))]</math>
 
 
====The Gumbel Failure Rate Function====
The instantaneous Gumbel failure rate is given by:
 
<math>\lambda =\frac{{{e}^{z}}}{\sigma }</math>
 
 
====Characteristics of the Gumbel Distribution====
Some of the specific characteristics of the Gumbel distribution are the following:
 
• The shape of the Gumbel distribution is skewed to the left. The Gumbel  <math>pdf</math>  has no shape parameter. This means that the Gumbel  <math>pdf</math>  has only one shape, which does not change.
 
• The Gumbel  <math>pdf</math>  has location parameter  <math>\mu ,</math>  which is equal to the mode  <math>\tilde{T},</math>  but it differs from median and mean. This is because the Gumbel distribution is not symmetrical about its  <math>\mu </math> .
 
• As  <math>\mu </math>  decreases, the  <math>pdf</math>  is shifted to the left.
 
• As  <math>\mu </math>  increases, the  <math>pdf</math>  is shifted to the right.
 
• As  <math>\sigma </math>  increases, the  <math>pdf</math>  spreads out and becomes shallower.
 
• As  <math>\sigma </math>  decreases, the  <math>pdf</math>  becomes taller and narrower.
 
• For  <math>T=\pm \infty ,</math>  <math>pdf=0.</math>  For  <math>T=\mu </math> , the  <math>pdf</math>  reaches its maximum point <math>\frac{1}{\sigma e}</math>
 
• The points of inflection of the  <math>pdf</math>  graph are  <math>T=\mu \pm \sigma \ln (\tfrac{3\pm \sqrt{5}}{2})</math>  or  <math>T\approx \mu \pm \sigma 0.96242</math> .
 
• If times follow the Weibull distribution, then the logarithm of times follow a Gumbel distribution. If  <math>{{t}_{i}}</math>  follows a Weibull distribution with  <math>\beta </math>  and  <math>\eta </math>  , then the  <math>Ln({{t}_{i}})</math>  follows a Gumbel distribution with  <math>\mu =\ln (\eta )</math>  and  <math>\sigma =\tfrac{1}{\beta }</math>  [32] <math>.</math>
 
====Probability Paper====
The form of the Gumbel probability paper is based on a linearization of the  <math>cdf</math> . From Eqn. (UnrGumbel):
 
<math>z=\ln (-\ln (1-F))</math>
 
 
using Eqns. (z3):
 
<math>\frac{T-\mu }{\sigma }=\ln (-\ln (1-F))</math>
 
 
Then:
 
<math>\ln (-\ln (1-F))=-\frac{\mu }{\sigma }+\frac{1}{\sigma }T</math>
 
 
Now let:
 
<math>y=\ln (-\ln (1-F))</math>
 
 
<math>x=T</math>
 
 
and:
 
<math>\begin{align}
  & a= & -\frac{\mu }{\sigma } \\
& b= & \frac{1}{\sigma } 
\end{align}</math>
 
 
which results in the linear equation of:
 
<math>y=a+bx</math>
 
 
The Gumbel probability paper resulting from this linearized  <math>cdf</math>  function is shown next.
 
 
For  <math>z=0</math> ,  <math>T=\mu </math>  and  <math>R(t)={{e}^{-{{e}^{0}}}}\approx 0.3678</math>  (63.21% unreliability). For  <math>z=1</math> ,  <math>\sigma =T-\mu </math>  and  <math>R(t)={{e}^{-{{e}^{1}}}}\approx 0.0659.</math>  To read  <math>\mu </math>  from the plot, find the time value that corresponds to the intersection of the probability plot with the 63.21% unreliability line. To read  <math>\sigma </math>  from the plot, find the time value that corresponds to the intersection of the probability plot with the 93.40% unreliability line, then take the difference between this time value and the  <math>\mu </math>  value.
====Confidence Bounds====
This section presents the method used by the application to estimate the different types of confidence bounds for data that follow the Gumbel distribution. The complete derivations were presented in detail (for a general function) in Chapter 5. Only Fisher Matrix confidence bounds are available for the Gumbel distribution.
====Bounds on the Parameters====
The lower and upper bounds on the mean,  <math>\widehat{\mu }</math> , are estimated from:
 
<math>\begin{align}
  & {{\mu }_{U}}= & \widehat{\mu }+{{K}_{\alpha }}\sqrt{Var(\widehat{\mu })}\text{ (upper bound)} \\
& {{\mu }_{L}}= & \widehat{\mu }-{{K}_{\alpha }}\sqrt{Var(\widehat{\mu })}\text{ (lower bound)} 
\end{align}</math>
 
 
Since the standard deviation,  <math>\widehat{\sigma }</math> , must be positive, then  <math>\ln (\widehat{\sigma })</math>  is treated as normally distributed, and the bounds are estimated from:
 
<math>\begin{align}
  & {{\sigma }_{U}}= & \widehat{\sigma }\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{\sigma })}}{{{\widehat{\sigma }}_{T}}}}}\text{ (upper bound)} \\
& {{\sigma }_{L}}= & \frac{\widehat{\sigma }}{{{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{\sigma })}}{\widehat{\sigma }}}}}\text{ (lower bound)} 
\end{align}</math>
 
where  <math>{{K}_{\alpha }}</math>  is defined by:
 
<math>\alpha =\frac{1}{\sqrt{2\pi }}\int_{{{K}_{\alpha }}}^{\infty }{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt=1-\Phi ({{K}_{\alpha }})</math>
 
 
If  <math>\delta </math>  is the confidence level, then  <math>\alpha =\tfrac{1-\delta }{2}</math>  for the two-sided bounds, and  <math>\alpha =1-\delta </math>  for the one-sided bounds.
 
The variances and covariances of  <math>\widehat{\mu }</math>  and  <math>\widehat{\sigma }</math>  are estimated from the Fisher matrix as follows:
 
<math>\left( \begin{matrix}
  \widehat{Var}\left( \widehat{\mu } \right) & \widehat{Cov}\left( \widehat{\mu },\widehat{\sigma } \right)  \\
  \widehat{Cov}\left( \widehat{\mu },\widehat{\sigma } \right) & \widehat{Var}\left( \widehat{\sigma } \right)  \\
\end{matrix} \right)=\left( \begin{matrix}
  -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\mu }^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \mu \partial \sigma }  \\
  {} & {}  \\
  -\tfrac{{{\partial }^{2}}\Lambda }{\partial \mu \partial \sigma } & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\sigma }^{2}}}  \\
\end{matrix} \right)_{\mu =\widehat{\mu },\sigma =\widehat{\sigma }}^{-1}</math>
 
 
<math>\Lambda </math>  is the log-likelihood function of the Gumbel distribution, described in Chapter 3 and Appendix C.
 
====Bounds on Reliability====
The reliability of the Gumbel distribution is given by: 
 
<math>\widehat{R}(T;\hat{\mu },\hat{\sigma })={{e}^{-{{e}^{{\hat{z}}}}}}</math>
 
where:
 
<math>\widehat{z}=\frac{t-\widehat{\mu }}{\widehat{\sigma }}</math>
 
 
The bounds on  <math>z</math>  are estimated from:
 
<math>\begin{align}
  & {{z}_{U}}= & \widehat{z}+{{K}_{\alpha }}\sqrt{Var(\widehat{z})} \\
& {{z}_{L}}= & \widehat{z}-{{K}_{\alpha }}\sqrt{Var(\widehat{z})} 
\end{align}</math>
 
where:
 
<math>Var(\widehat{z})={{\left( \frac{\partial z}{\partial \mu } \right)}^{2}}Var(\widehat{\mu })+{{\left( \frac{\partial z}{\partial \sigma } \right)}^{2}}Var(\widehat{\sigma })+2\left( \frac{\partial z}{\partial \mu } \right)\left( \frac{\partial z}{\partial \sigma } \right)Cov\left( \widehat{\mu },\widehat{\sigma } \right)</math>
 
or:
 
<math>Var(\widehat{z})=\frac{1}{{{\widehat{\sigma }}^{2}}}\left[ Var(\widehat{\mu })+{{\widehat{z}}^{2}}Var(\widehat{\sigma })+2\cdot \widehat{z}\cdot Cov\left( \widehat{\mu },\widehat{\sigma } \right) \right]</math>
 
 
The upper and lower bounds on reliability are:
 
<math>\begin{align}
  & {{R}_{U}}= & {{e}^{-{{e}^{{{z}_{L}}}}}}\text{ (upper bound)} \\
& {{R}_{L}}= & {{e}^{-{{e}^{{{z}_{U}}}}}}\text{ (lower bound)} 
\end{align}</math>
 
====Bounds on Time====
The bounds around time for a given Gumbel percentile (unreliability) are estimated by first solving the reliability equation with respect to time, as follows:
 
<math>\widehat{T}(\widehat{\mu },\widehat{\sigma })=\widehat{\mu }+\widehat{\sigma }z</math>
 
 
where:
 
<math>z=\ln (-\ln (R))</math>
 
 
<math>Var(\widehat{T})={{(\frac{\partial T}{\partial \mu })}^{2}}Var(\widehat{\mu })+2(\frac{\partial T}{\partial \mu })(\frac{\partial T}{\partial \sigma })Cov(\widehat{\mu },\widehat{\sigma })+{{(\frac{\partial T}{\partial \sigma })}^{2}}Var(\widehat{\sigma })</math>
 
 
or:
 
<math>Var(\widehat{T})=Var(\widehat{\mu })+2\widehat{z}Cov(\widehat{\mu },\widehat{\sigma })+{{\widehat{z}}^{2}}Var(\widehat{\sigma })</math>
 
 
The upper and lower bounds are then found by:
 
<math>\begin{align}
  & {{T}_{U}}= & \hat{T}+{{K}_{\alpha }}\sqrt{Var(\hat{T})}\text{ (Upper bound)} \\
& {{T}_{L}}= & \hat{T}-{{K}_{\alpha }}\sqrt{Var(\hat{T})}\text{ (Lower bound)} 
\end{align}</math>
 
 
====A Gumbel Distribution Example====
Verify using Monte Carlo simulation that if  <math>{{t}_{i}}</math>  follows a Weibull distribution with  <math>\beta </math>  and  <math>\eta </math> , then the  <math>Ln({{t}_{i}})</math>  follows a Gumbel distribution with  <math>\mu =\ln (\eta )</math>  and  <math>\sigma =1/\beta ).</math>
Let us assume that  <math>{{t}_{i}}</math>  follows a Weibull distribution with  <math>\beta =0.5</math>  and  <math>\eta =10000.</math>  The Monte Carlo simulation tool in Weibull++ can be used to generate a set of random numbers that follow a Weibull distribution with the specified parameters.
 
 
After obtaining the random time values  <math>{{t}_{i}}</math> , insert a new Data Sheet using the Insert Data Sheet option under the Folio menu. In this sheet enter the  <math>Ln({{t}_{i}})</math>  values using the LN function and referring to the cells in the sheet that contains the  <math>{{t}_{i}}</math>  values. Delete any negative values, if there are any, since Weibull++ expects time values to be positive. Calculate the parameters of the Gumbel distribution that fits the  <math>Ln({{t}_{i}})</math>  values.
 
Using maximum likelihood as the analysis method, the estimated parameters are:
 
<math>\begin{align}
  & \hat{\mu }= & 9.3816 \\
& \hat{\sigma }= & 1.9717 
\end{align}</math>


::<math>{{T}_{L}}={{e}^{{{u}_{L}}}}\text{ (lower bound)}\,\!</math>


Since  <math>\ln (\eta )=</math>  9.2103 ( <math>\simeq 9.3816</math> ) and  <math>1/\beta =2</math>  <math>(\simeq 1.9717),</math>  then this simulation verifies that  <math>Ln({{t}_{i}})</math>  follows a Gumbel distribution with  <math>\mu =\ln (\eta )</math>  and  <math>\delta =1/\beta .</math>
==General Examples==
Note: This example illustrates a property of the Gumbel distribution; it is not meant to be a formal proof.
{{:Loglogistic Distribution Example}}

Latest revision as of 17:12, 23 December 2015

New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images, more targeted search and the latest content available as a PDF. As of September 2023, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest reference at help.reliasoft.com/reference/life_data_analysis

Chapter 15: The Loglogistic Distribution


Weibullbox.png

Chapter 15  
The Loglogistic Distribution  

Synthesis-icon.png

Available Software:
Weibull++

Examples icon.png

More Resources:
Weibull++ Examples Collection

As may be indicated by the name, the loglogistic distribution has certain similarities to the logistic distribution. A random variable is loglogistically distributed if the logarithm of the random variable is logistically distributed. Because of this, there are many mathematical similarities between the two distributions, as discussed in Meeker and Escobar [27]. For example, the mathematical reasoning for the construction of the probability plotting scales is very similar for these two distributions.

Loglogistic Probability Density Function

The loglogistic distribution is a 2-parameter distribution with parameters [math]\displaystyle{ \mu \,\! }[/math] and [math]\displaystyle{ \sigma \,\! }[/math]. The pdf for this distribution is given by:

[math]\displaystyle{ f(t)=\frac{{{e}^{z}}}{\sigma {t}{{(1+{{e}^{z}})}^{2}}}\,\! }[/math]

where:

[math]\displaystyle{ z=\frac{{t}'-\mu }{\sigma }\,\! }[/math]
[math]\displaystyle{ {t}'=\ln (t)\,\! }[/math]

and:

[math]\displaystyle{ \begin{align} & \mu = & \text{scale parameter} \\ & \sigma = & \text{shape parameter} \end{align}\,\! }[/math]

where [math]\displaystyle{ 0\lt t\lt \infty \,\! }[/math], [math]\displaystyle{ -\infty \lt \mu \lt \infty \,\! }[/math] and [math]\displaystyle{ 0\lt \sigma \lt \infty \,\! }[/math].

Mean, Median and Mode

The mean of the loglogistic distribution, [math]\displaystyle{ \overline{T}\,\! }[/math], is given by:

[math]\displaystyle{ \overline{T}={{e}^{\mu }}\Gamma (1+\sigma )\Gamma (1-\sigma )\,\! }[/math]

Note that for [math]\displaystyle{ \sigma \ge 1,\,\! }[/math] [math]\displaystyle{ \overline{T}\,\! }[/math] does not exist.

The median of the loglogistic distribution, [math]\displaystyle{ \breve{T}\,\! }[/math], is given by:

[math]\displaystyle{ \widehat{T}={{e}^{\mu }}\,\! }[/math]

The mode of the loglogistic distribution, [math]\displaystyle{ \tilde{T}\,\! }[/math], if [math]\displaystyle{ \sigma \lt 1,\,\! }[/math] is given by:

[math]\displaystyle{ \tilde{T} = e^{\mu+\sigma ln(\frac{1-\sigma}{1+\sigma})}\,\! }[/math]

The Standard Deviation

The standard deviation of the loglogistic distribution, [math]\displaystyle{ {{\sigma }_{T}}\,\! }[/math], is given by:

[math]\displaystyle{ {{\sigma }_{T}}={{e}^{\mu }}\sqrt{\Gamma (1+2\sigma )\Gamma (1-2\sigma )-{{(\Gamma (1+\sigma )\Gamma (1-\sigma ))}^{2}}}\,\! }[/math]

Note that for [math]\displaystyle{ \sigma \ge 0.5,\,\! }[/math] the standard deviation does not exist.

The Loglogistic Reliability Function

The reliability for a mission of time [math]\displaystyle{ T\,\! }[/math], starting at age 0, for the loglogistic distribution is determined by:

[math]\displaystyle{ R=\frac{1}{1+{{e}^{z}}}\,\! }[/math]

where:

[math]\displaystyle{ z=\frac{{t}'-\mu }{\sigma }\,\! }[/math]
[math]\displaystyle{ \begin{align} {t}'=\ln (t) \end{align}\,\! }[/math]

The unreliability function is:

[math]\displaystyle{ F=\frac{{{e}^{z}}}{1+{{e}^{z}}}\,\! }[/math]

The loglogistic Reliable Life

The logistic reliable life is:

[math]\displaystyle{ \begin{align} {{T}_{R}}={{e}^{\mu +\sigma [\ln (1-R)-\ln (R)]}} \end{align}\,\! }[/math]

The loglogistic Failure Rate Function

The loglogistic failure rate is given by:

[math]\displaystyle{ \lambda (t)=\frac{{{e}^{z}}}{\sigma t(1+{{e}^{z}})}\,\! }[/math]

Distribution Characteristics

For [math]\displaystyle{ \sigma \gt 1\,\! }[/math] :

  • [math]\displaystyle{ f(t)\,\! }[/math] decreases monotonically and is convex. Mode and mean do not exist.

For [math]\displaystyle{ \sigma =1\,\! }[/math] :

  • [math]\displaystyle{ f(t)\,\! }[/math] decreases monotonically and is convex. Mode and mean do not exist. As [math]\displaystyle{ t\to 0\,\! }[/math], [math]\displaystyle{ f(t)\to \tfrac{1}{\sigma {{e}^{\tfrac{\mu }{\sigma }}}}.\,\! }[/math]
  • As [math]\displaystyle{ t\to 0\,\! }[/math], [math]\displaystyle{ \lambda (t)\to \tfrac{1}{\sigma {{e}^{\tfrac{\mu }{\sigma }}}}.\,\! }[/math]

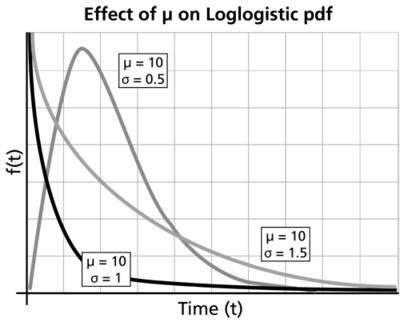
For [math]\displaystyle{ 0\lt \sigma \lt 1\,\! }[/math] :

  • The shape of the loglogistic distribution is very similar to that of the lognormal distribution and the Weibull distribution.
  • The pdf starts at zero, increases to its mode, and decreases thereafter.
  • As [math]\displaystyle{ \mu \,\! }[/math] increases, while [math]\displaystyle{ \sigma \,\! }[/math] is kept the same, the pdf gets stretched out to the right and its height decreases, while maintaining its shape.
  • As [math]\displaystyle{ \mu \,\! }[/math] decreases,while [math]\displaystyle{ \sigma \,\! }[/math] is kept the same, the pdf gets pushed in towards the left and its height increases.
  • [math]\displaystyle{ \lambda (t)\,\! }[/math] increases till [math]\displaystyle{ t={{e}^{\mu +\sigma \ln (\tfrac{1-\sigma }{\sigma })}}\,\! }[/math] and decreases thereafter. [math]\displaystyle{ \lambda (t)\,\! }[/math] is concave at first, then becomes convex.
WB.15 loglogistic pdf.png

Confidence Bounds

The method used by the application in estimating the different types of confidence bounds for loglogistically distributed data is presented in this section. The complete derivations were presented in detail for a general function in Parameter Estimation.

Bounds on the Parameters

The lower and upper bounds [math]\displaystyle{ {\mu }\,\! }[/math], are estimated from:

[math]\displaystyle{ \begin{align} & \mu _{U}= & {{\widehat{\mu }}}+{{K}_{\alpha }}\sqrt{Var(\widehat{\mu })}\text{ (upper bound)} \\ & \mu _{L}= & {{\widehat{\mu }}}-{{K}_{\alpha }}\sqrt{Var(\widehat{\mu })}\text{ (lower bound)} \end{align}\,\! }[/math]

For paramter [math]\displaystyle{ {{\widehat{\sigma }}}\,\! }[/math], [math]\displaystyle{ \ln ({{\widehat{\sigma }}})\,\! }[/math] is treated as normally distributed, and the bounds are estimated from:

[math]\displaystyle{ \begin{align} & {{\sigma }_{U}}= & {{\widehat{\sigma }}}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{\sigma })}}{\widehat{\sigma }}}}\text{ (upper bound)} \\ & {{\sigma }_{L}}= & \frac{{{\widehat{\sigma }}}}{{{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{\sigma })}}{{{\widehat{\sigma }}}}}}}\text{ (lower bound)} \end{align}\,\! }[/math]

where [math]\displaystyle{ {{K}_{\alpha }}\,\! }[/math] is defined by:

[math]\displaystyle{ \alpha =\frac{1}{\sqrt{2\pi }}\int_{{{K}_{\alpha }}}^{\infty }{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt=1-\Phi ({{K}_{\alpha }})\,\! }[/math]

If [math]\displaystyle{ \delta \,\! }[/math] is the confidence level, then [math]\displaystyle{ \alpha =\tfrac{1-\delta }{2}\,\! }[/math] for the two-sided bounds, and [math]\displaystyle{ \alpha =1-\delta \,\! }[/math] for the one-sided bounds.

The variances and covariances of [math]\displaystyle{ \widehat{\mu }\,\! }[/math] and [math]\displaystyle{ \widehat{\sigma }\,\! }[/math] are estimated as follows:

[math]\displaystyle{ \left( \begin{matrix} \widehat{Var}\left( \widehat{\mu } \right) & \widehat{Cov}\left( \widehat{\mu },\widehat{\sigma } \right) \\ \widehat{Cov}\left( \widehat{\mu },\widehat{\sigma } \right) & \widehat{Var}\left( \widehat{\sigma } \right) \\ \end{matrix} \right)=\left( \begin{matrix} -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{(\mu )}^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \mu \partial \sigma } \\ {} & {} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial \mu \partial \sigma } & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\sigma }^{2}}} \\ \end{matrix} \right)_{\mu =\widehat{\mu },\sigma =\widehat{\sigma }}^{-1}\,\! }[/math]

where [math]\displaystyle{ \Lambda \,\! }[/math] is the log-likelihood function of the loglogistic distribution.

Bounds on Reliability

The reliability of the logistic distribution is:

[math]\displaystyle{ \widehat{R}=\frac{1}{1+\exp (\widehat{z})}\,\! }[/math]

where:

[math]\displaystyle{ \widehat{z}=\frac{{t}'-\widehat{\mu }}{\widehat{\sigma }}\,\! }[/math]

Here [math]\displaystyle{ 0\lt t\lt \infty \,\! }[/math], [math]\displaystyle{ -\infty \lt \mu \lt \infty \,\! }[/math], [math]\displaystyle{ 0\lt \sigma \lt \infty \,\! }[/math], therefore [math]\displaystyle{ 0\lt t'=\ln (t)\lt \infty \,\! }[/math] and [math]\displaystyle{ z\,\! }[/math] also is changing from [math]\displaystyle{ -\infty \,\! }[/math] till [math]\displaystyle{ +\infty \,\! }[/math].

The bounds on [math]\displaystyle{ z\,\! }[/math] are estimated from:

[math]\displaystyle{ {{z}_{U}}=\widehat{z}+{{K}_{\alpha }}\sqrt{Var(\widehat{z})}\,\! }[/math]
[math]\displaystyle{ {{z}_{L}}=\widehat{z}-{{K}_{\alpha }}\sqrt{Var(\widehat{z})\text{ }}\text{ }\,\! }[/math]

where:

[math]\displaystyle{ Var(\widehat{z})={{(\frac{\partial z}{\partial \mu })}^{2}}Var({{\widehat{\mu }}^{\prime }})+2(\frac{\partial z}{\partial \mu })(\frac{\partial z}{\partial \sigma })Cov(\widehat{\mu },\widehat{\sigma })+{{(\frac{\partial z}{\partial \sigma })}^{2}}Var(\widehat{\sigma })\,\! }[/math]

or:

[math]\displaystyle{ Var(\widehat{z})=\frac{1}{{{\sigma }^{2}}}(Var(\widehat{\mu })+2\widehat{z}Cov(\widehat{\mu },\widehat{\sigma })+{{\widehat{z}}^{2}}Var(\widehat{\sigma }))\,\! }[/math]

The upper and lower bounds on reliability are:

[math]\displaystyle{ {{R}_{U}}=\frac{1}{1+{{e}^{{{z}_{L}}}}}\text{(Upper bound)}\,\! }[/math]
[math]\displaystyle{ {{R}_{L}}=\frac{1}{1+{{e}^{{{z}_{U}}}}}\text{(Lower bound)}\,\! }[/math]

Bounds on Time

The bounds around time for a given loglogistic percentile, or unreliability, are estimated by first solving the reliability equation with respect to time, as follows:

[math]\displaystyle{ \widehat{T}(\widehat{\mu },\widehat{\sigma })={{e}^{\widehat{\mu }+\widehat{\sigma }z}}\,\! }[/math]

where:

[math]\displaystyle{ \begin{align} z=\ln (1-R)-\ln (R) \end{align}\,\! }[/math]

or:

[math]\displaystyle{ \ln (\hat{T})=\widehat{\mu }+\widehat{\sigma }z\,\! }[/math]

Let:

[math]\displaystyle{ {u}=\ln (\hat{T})=\widehat{\mu }+\widehat{\sigma }z\,\! }[/math]

then:

[math]\displaystyle{ {u}_{U}=\widehat{u}+{{K}_{\alpha }}\sqrt{Var(\widehat{u})\text{ }}\text{ }\,\! }[/math]


[math]\displaystyle{ {u}_{L}=\widehat{u}-{{K}_{\alpha }}\sqrt{Var(\widehat{u})\text{ }}\text{ }\,\! }[/math]

where:

[math]\displaystyle{ Var(\widehat{u})={{(\frac{\partial u}{\partial \mu })}^{2}}Var(\widehat{\mu })+2(\frac{\partial u}{\partial \mu })(\frac{\partial u}{\partial \sigma })Cov(\widehat{\mu },\widehat{\sigma })+{{(\frac{\partial u}{\partial \sigma })}^{2}}Var(\widehat{\sigma })\,\! }[/math]

or:

[math]\displaystyle{ Var(\widehat{u})=Var(\widehat{\mu })+2\widehat{z}Cov(\widehat{\mu },\widehat{\sigma })+{{\widehat{z}}^{2}}Var(\widehat{\sigma })\,\! }[/math]

The upper and lower bounds are then found by:

[math]\displaystyle{ {{T}_{U}}={{e}^{{{u}_{U}}}}\text{ (upper bound)}\,\! }[/math]
[math]\displaystyle{ {{T}_{L}}={{e}^{{{u}_{L}}}}\text{ (lower bound)}\,\! }[/math]

General Examples

Determine the loglogistic parameter estimates for the data given in the following table.

[math]\displaystyle{ \overset{{}}{\mathop{\text{Test data}}}\,\,\! }[/math]
[math]\displaystyle{ \begin{matrix} \text{Data point index} & \text{Last Inspected} & \text{State End time} \\ \text{1} & \text{105} & \text{106} \\ \text{2} & \text{197} & \text{200} \\ \text{3} & \text{297} & \text{301} \\ \text{4} & \text{330} & \text{335} \\ \text{5} & \text{393} & \text{401} \\ \text{6} & \text{423} & \text{426} \\ \text{7} & \text{460} & \text{468} \\ \text{8} & \text{569} & \text{570} \\ \text{9} & \text{675} & \text{680} \\ \text{10} & \text{884} & \text{889} \\ \end{matrix}\,\! }[/math]


Set up the folio for times-to-failure data that includes interval and left censored data, then enter the data. The computed parameters for maximum likelihood are calculated to be:

[math]\displaystyle{ \begin{align} & {{{\hat{\mu }}}^{\prime }}= & 5.9772 \\ & {{{\hat{\sigma }}}_{{{T}'}}}= & 0.3256 \end{align}\,\! }[/math]

For rank regression on [math]\displaystyle{ X\,\! }[/math]:

[math]\displaystyle{ \begin{align} & \hat{\mu }= & 5.9281 \\ & \hat{\sigma }= & 0.3821 \end{align}\,\! }[/math]

For rank regression on [math]\displaystyle{ Y\,\! }[/math]:

[math]\displaystyle{ \begin{align} & \hat{\mu }= & 5.9772 \\ & \hat{\sigma }= & 0.3256 \end{align}\,\! }[/math]
Retrieved from "https://www.reliawiki.com/index.php?title=The_Loglogistic_Distribution&oldid=62255"