Reliability Data - Logistic Model

New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.

As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at RGA examples and RGA reference examples.

---

This example appears in the Reliability growth reference.

Using the reliability growth data given in the table below, do the following:

1. Find a Gompertz curve that represents the data and plot it with the raw data.
2. Find a Logistic reliability growth curve that represents the data and plot it with the raw data.

Development Time vs. Observed Reliability data and Predicted Reliabilities

Time, months	Raw Data Reliability (%)	Gompertz Reliability (%)	Logistic Reliablity (%)
0	31.00	24.85	22.73
1	35.50	38.48	38.14
2	49.30	51.95	56.37
3	70.10	63.82	73.02
4	83.00	73.49	85.01
5	92.20	80.95	92.24
6	96.40	86.51	96.14
7	98.60	90.54	98.12
8	99.00	93.41	99.09

Solution

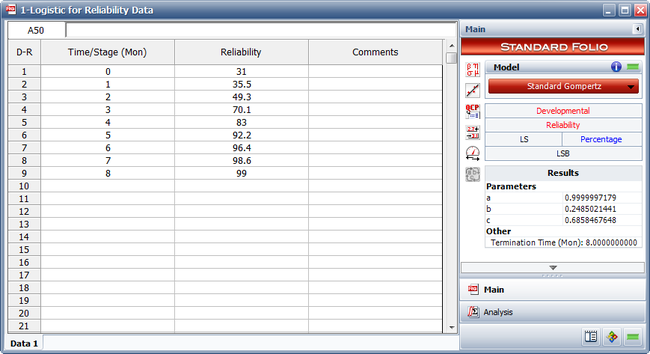
1. The figure below shows the entered data and the estimated parameters using the standard Gompertz model.
   

   Therefore:

   [math]\displaystyle{ \begin{align} & \widehat{a}= & 0.9999 \\ & \widehat{b}= & 0.2485 \\ & \widehat{c}= & 0.6858 \end{align}\,\! }[/math]

   [math]\displaystyle{ R=(0.9999){{(0.2485)}^{{{0.6858}^{T}}}}\,\! }[/math]

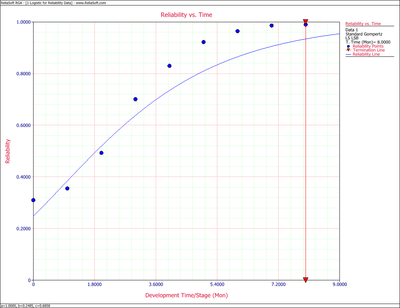
   The values of the predicted reliabilities are plotted in the figure below.

   

   Notice how the standard Gompertz model is not really capable of handling the S-shaped characteristics of this data.

2. The least squares estimators of the Logistic growth curve parameters are given by Crow [9]: where:

   [math]\displaystyle{ \begin{align} {{{\hat{b}}}_{1}}= & \frac{\underset{i=0}{\overset{N-1}{\mathop{\sum }}}\,{{T}_{i}}{{Y}_{i}}-N\cdot \bar{T}\cdot \bar{Y}}{\underset{i=0}{\overset{N-1}{\mathop{\sum }}}\,T_{i}^{2}-N\cdot {{{\bar{T}}}^{2}}} \\ \\ {{{\hat{b}}}_{0}}= & \bar{Y}-{{{\hat{b}}}_{1}}\bar{T} \\ \\ {{Y}_{i}}= & \ln \left( \frac{1}{{{R}_{i}}}-1 \right) \\ \\ \bar{Y}= & \frac{1}{N}\underset{i=0}{\overset{N-1}{\mathop \sum }}\,{{Y}_{i}} \end{align}\,\! }[/math]

   In this example [math]\displaystyle{ N=9\,\! }[/math], which gives:

   [math]\displaystyle{ \begin{align} \overline{Y}&=\frac{1}{9}\sum_{i=0}^{8}ln\left (\frac{1}{R_{i}}-1 \right ) \\ &= -1.7355 \\ \\ \overline{T}&=\frac{1}{9}\sum_{i=0}^{8}T_{i} = 4 \\ \sum_{i=0}^{8}T_{i}^{2} &= 204 \\ \sum_{i=0}^{8}T_{i}Y_{i} &= -106.8630 \end{align}\,\! }[/math]

   From the equations for [math]\displaystyle{ b_{i}\,\! }[/math] and [math]\displaystyle{ \hat{b_{0}}\,\! }[/math]:

   [math]\displaystyle{ \begin{align} \hat{b_{1}} &= \frac{-106.8630 - 9(4)(-1.7355)}{204-9(4)_{2}} \\ & = 0.7398 \\ \hat{b_{0}} &= -1.7355 - (-0.7398)(4)\\ &= 1.2235 \end{align}\,\! }[/math]

   And from the least squares estimators for [math]\displaystyle{ \hat{b}\,\! }[/math] and [math]\displaystyle{ \hat{k}\,\! }[/math]:

   [math]\displaystyle{ \begin{align} \widehat{b}= & {{e}^{1.2235}} \\ = & 3.3991 \\ \widehat{k}= & -(-0.7398) \\ = & 0.7398 \end{align}\,\! }[/math]

   Therefore, the Logistic reliability growth curve that represents this data set is given by:

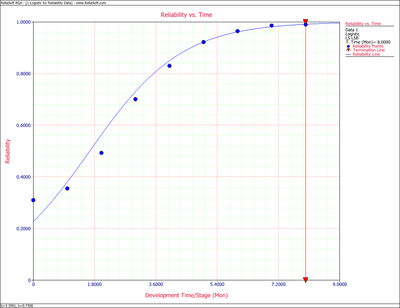
   [math]\displaystyle{ R=\frac{1}{1+3.3991\,{{e}^{-0.7398\,T}}}\,\! }[/math]

   The following figure shows the Reliability vs. Time plot. The plot shows that the observed data set is estimated well by the Logistic reliability growth curve, except in the region closely surrounding the inflection point of the observed reliability. This problem can be overcome by using the modified Gompertz model.