Weibull Parameter Estimation

Estimation of the Weibull Parameters

The estimates of the parameters of the Weibull distribution can be found graphically via probability plotting paper, or analytically, using either least squares (rank regression) or maximum likelihood estimation (MLE).

Probability Plotting

One method of calculating the parameters of the Weibull distribution is by using probability plotting. To better illustrate this procedure, consider the following example from Kececioglu [20].

Assume that six identical units are being reliability tested at the same application and operation stress levels. All of these units fail during the test after operating the following number of hours: 93, 34, 16, 120, 53 and 75. Estimate the values of the parameters for a 2-parameter Weibull distribution and determine the reliability of the units at a time of 15 hours.

Solution

The steps for determining the parameters of the Weibull representing the data, using probability plotting, are outlined in the following instructions. First, rank the times-to-failure in ascending order as shown next.

Time-to-failure, hours	Failure Order Number out of Sample Size of 6
16	1
34	2
53	3
75	4
93	5
120	6

Obtain their median rank plotting positions. Median rank positions are used instead of other ranking methods because median ranks are at a specific confidence level (50%). Median ranks can be found tabulated in many reliability books. They can also be estimated using the following equation:

[math]\displaystyle{ MR \sim { \frac{i-0.3}{N+0.4}}\cdot 100 \,\! }[/math]

where [math]\displaystyle{ i\,\! }[/math] is the failure order number and [math]\displaystyle{ N\,\! }[/math] is the total sample size. The exact median ranks are found in Weibull++ by solving:

[math]\displaystyle{ \sum_{k=i}^N{\binom{N}{k}}{MR^k}{(1-MR)^{N-k}}=0.5=50% \,\! }[/math]

for [math]\displaystyle{ MR\,\! }[/math], where [math]\displaystyle{ N\,\! }[/math] is the sample size and [math]\displaystyle{ i\,\! }[/math] the order number. The times-to-failure, with their corresponding median ranks, are shown next.

Time-to-failure, hours	Median Rank,%
16	10.91
34	26.44
53	42.14
75	57.86
93	73.56
120	89.1

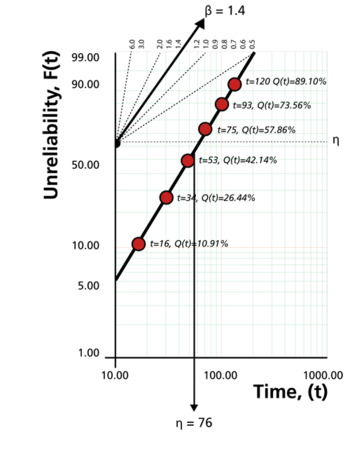
On a Weibull probability paper, plot the times and their corresponding ranks. A sample of a Weibull probability paper is given in the following figure.

The points of the data in the example are shown in the figure below. Draw the best possible straight line through these points, as shown below, then obtain the slope of this line by drawing a line, parallel to the one just obtained, through the slope indicator. This value is the estimate of the shape parameter [math]\displaystyle{ \hat{\beta } \,\! }[/math], in this case [math]\displaystyle{ \hat{\beta }=1.4 \,\! }[/math].

At the [math]\displaystyle{ Q(t)=63.2%\,\! }[/math] ordinate point, draw a straight horizontal line until this line intersects the fitted straight line. Draw a vertical line through this intersection until it crosses the abscissa. The value at the intersection of the abscissa is the estimate of [math]\displaystyle{ \hat{\eta } \,\! }[/math]. For this case, [math]\displaystyle{ \hat{\eta }=76 \,\! }[/math] hours. This is always at 63.2% since:

[math]\displaystyle{ Q(t)=1-e^{-(\frac{t}{\eta })^{\beta }}=1-e^{-1}=0.632=63.2% \,\! }[/math]

Now any reliability value for any mission time [math]\displaystyle{ t\,\! }[/math] can be obtained. For example, the reliability for a mission of 15 hours, or any other time, can now be obtained either from the plot or analytically. To obtain the value from the plot, draw a vertical line from the abscissa, at hours, to the fitted line. Draw a horizontal line from this intersection to the ordinate and read [math]\displaystyle{ Q(t)\,\! }[/math], in this case [math]\displaystyle{ Q(t)=9.8%\,\! }[/math]. Thus, [math]\displaystyle{ R(t)=1-Q(t)=90.2%\,\! }[/math]. This can also be obtained analytically from the Weibull reliability function since the estimates of both of the parameters are known or:

[math]\displaystyle{ R(t=15)=e^{-\left( \frac{15}{\eta }\right) ^{\beta }}=e^{-\left( \frac{15}{76 }\right) ^{1.4}}=90.2% \,\! }[/math]

Probability Plotting for the Location Parameter, Gamma

The third parameter of the Weibull distribution is utilized when the data do not fall on a straight line, but fall on either a concave up or down curve. The following statements can be made regarding the value of [math]\displaystyle{ \gamma \,\! }[/math]:

• Case 1: If the curve for MR versus [math]\displaystyle{ {{t}_{j}}\,\! }[/math] is concave down and the curve for MR versus [math]\displaystyle{ {({t}_{j}-{t}_{1})}\,\! }[/math] is concave up, then there exists a [math]\displaystyle{ \gamma \,\! }[/math] such that [math]\displaystyle{ 0\lt \gamma \lt t_{1}\,\! }[/math], or [math]\displaystyle{ \gamma \,\! }[/math] has a positive value.

• Case 2: If the curves for MR versus [math]\displaystyle{ {{t}_{j}}\,\! }[/math] and MR versus [math]\displaystyle{ {({t}_{j}-{t}_{1})}\,\! }[/math] are both concave up, then there exists a negative [math]\displaystyle{ \gamma \,\! }[/math] which will straighten out the curve of MR versus [math]\displaystyle{ {{t}_{j}}\,\! }[/math].

• Case 3: If neither one of the previous two cases prevails, then either reject the Weibull as one capable of representing the data, or proceed with the multiple population (mixed Weibull) analysis. To obtain the location parameter, [math]\displaystyle{ \gamma \,\! }[/math]:

• Subtract the same arbitrary value, [math]\displaystyle{ \gamma \,\! }[/math], from all the times to failure and replot the data.
• If the initial curve is concave up, subtract a negative [math]\displaystyle{ \gamma \,\! }[/math] from each failure time.
• If the initial curve is concave down, subtract a positive [math]\displaystyle{ \gamma \,\! }[/math] from each failure time.
• Repeat until the data plots on an acceptable straight line.
• The value of [math]\displaystyle{ \gamma \,\! }[/math] is the subtracted (positive or negative) value that places the points in an acceptable straight line.

The other two parameters are then obtained using the techniques previously described. Also, it is important to note that we used the term subtract a positive or negative gamma, where subtracting a negative gamma is equivalent to adding it. Note that when adjusting for gamma, the x-axis scale for the straight line becomes [math]\displaystyle{ {({t}-\gamma)}\,\! }[/math].

Rank Regression on Y

Performing rank regression on Y requires that a straight line mathematically be fitted to a set of data points such that the sum of the squares of the vertical deviations from the points to the line is minimized. This is in essence the same methodology as the probability plotting method, except that we use the principle of least squares to determine the line through the points, as opposed to just eyeballing it. The first step is to bring our function into a linear form. For the two-parameter Weibull distribution, the (cumulative density function) is:

[math]\displaystyle{ F(t)=1-e^{-\left( \frac{t}{\eta }\right) ^{\beta }} \,\! }[/math]

Taking the natural logarithm of both sides of the equation yields:

[math]\displaystyle{ \ln[ 1-F(t)] =-( \frac{t}{\eta }) ^{\beta } \,\! }[/math]

[math]\displaystyle{ \ln{ -\ln[ 1-F(t)]} =\beta \ln ( \frac{t}{ \eta }) \,\! }[/math]

or:

[math]\displaystyle{ \begin{align} \ln \{ -\ln[ 1-F(t)]\} =-\beta \ln (\eta )+\beta \ln (t) \end{align}\,\! }[/math]

Now let:

[math]\displaystyle{ \begin{align} y = \ln \{ -\ln[ 1-F(t)]\} \end{align}\,\! }[/math]

[math]\displaystyle{ \begin{align} a = - \beta \ln(\eta) \end{align}\,\! }[/math]

and:

[math]\displaystyle{ \begin{align} b= \beta \end{align}\,\! }[/math]

which results in the linear equation of:

[math]\displaystyle{ \begin{align} y=a+bx \end{align}\,\! }[/math]

The least squares parameter estimation method (also known as regression analysis) was discussed in Parameter Estimation, and the following equations for regression on Y were derived:

[math]\displaystyle{ \hat{a}=\frac{\sum\limits_{i=1}^{N}y_{i}}{N}-\hat{b}\frac{ \sum\limits_{i=1}^{N}x_{i}}{N}=\bar{y}-\hat{b}\bar{x} \,\! }[/math]

and:

[math]\displaystyle{ \hat{b}={\frac{\sum\limits_{i=1}^{N}x_{i}y_{i}-\frac{\sum \limits_{i=1}^{N}x_{i}\sum\limits_{i=1}^{N}y_{i}}{N}}{\sum \limits_{i=1}^{N}x_{i}^{2}-\frac{\left( \sum\limits_{i=1}^{N}x_{i}\right) ^{2}}{N}}} \,\! }[/math]

In this case the equations for [math]\displaystyle{ {{y}_{i}}\,\! }[/math] and [math]\displaystyle{ {{x}_{i}}\,\! }[/math] are:

[math]\displaystyle{ y_{i}=\ln \left\{ -\ln [1-F(t_{i})]\right\} \,\! }[/math]

and:

[math]\displaystyle{ \begin{align} x_{i}=\ln(t_{i}) \end{align}\,\! }[/math]

The [math]\displaystyle{ F(t_{i})\,\! }[/math] values are estimated from the median ranks.

Once [math]\displaystyle{ \hat{a} \,\! }[/math] and [math]\displaystyle{ \hat{b} \,\! }[/math] are obtained, then [math]\displaystyle{ \hat{\beta } \,\! }[/math] and [math]\displaystyle{ \hat{\eta } \,\! }[/math] can easily be obtained from previous equations.

The Correlation Coefficient

The correlation coefficient is defined as follows:

[math]\displaystyle{ \rho ={\frac{\sigma _{xy}}{\sigma _{x}\sigma _{y}}} \,\! }[/math]

where [math]\displaystyle{ \sigma_{xy}\,\! }[/math] = covariance of [math]\displaystyle{ x\,\! }[/math] and [math]\displaystyle{ y\,\! }[/math], [math]\displaystyle{ \sigma_{x}\,\! }[/math] = standard deviation of [math]\displaystyle{ x\,\! }[/math], and [math]\displaystyle{ \sigma_{y}\,\! }[/math] = standard deviation of [math]\displaystyle{ y\,\! }[/math]. The estimator of [math]\displaystyle{ \rho\,\! }[/math] is the sample correlation coefficient, [math]\displaystyle{ \hat{\rho} \,\! }[/math], given by:

[math]\displaystyle{ \hat{\rho}=\frac{\sum\limits_{i=1}^{N}(x_{i}-\overline{x})(y_{i}-\overline{y} )}{\sqrt{\sum\limits_{i=1}^{N}(x_{i}-\overline{x})^{2}\cdot \sum\limits_{i=1}^{N}(y_{i}-\overline{y})^{2}}}\,\! }[/math]

RRY Example

Consider the same data set from the probability plotting example given above (with six failures at 16, 34, 53, 75, 93 and 120 hours). Estimate the parameters and the correlation coefficient using rank regression on Y, assuming that the data follow the 2-parameter Weibull distribution.

Solution

Construct a table as shown next.

Least Squares Analysis
[math]\displaystyle{ N\,\! }[/math]	[math]\displaystyle{ T_{i}\,\! }[/math]	[math]\displaystyle{ ln(T_{i})\,\! }[/math]	[math]\displaystyle{ F(T_i)\,\! }[/math]	[math]\displaystyle{ y_{i}\,\! }[/math]	[math]\displaystyle{ (ln{T_i})^2\,\! }[/math]	[math]\displaystyle{ {y_i}^2\,\! }[/math]	[math]\displaystyle{ (ln{T_i})y_i\,\! }[/math]
1	16	2.7726	0.1091	-2.1583	7.6873	4.6582	-5.9840
2	34	3.5264	0.2645	-1.1802	12.4352	1.393	-4.1620
3	53	3.9703	0.4214	-0.6030	15.7632	0.3637	-2.3943
4	75	4.3175	0.5786	-0.146	18.6407	0.0213	-0.6303
5	93	4.5326	0.7355	0.2851	20.5445	0.0813	1.2923
6	120	4.7875	0.8909	0.7955	22.9201	0.6328	3.8083
[math]\displaystyle{ \sum\,\! }[/math]		23.9068		-3.007	97.9909	7.1502	-8.0699

Utilizing the values from the table, calculate [math]\displaystyle{ \hat{a} \,\! }[/math] and [math]\displaystyle{ \hat{b} \,\! }[/math] using the following equations:

[math]\displaystyle{ \hat{b} =\frac{\sum\limits_{i=1}^{6}(\ln t_{i})y_{i}-(\sum\limits_{i=1}^{6}\ln t_{i})(\sum\limits_{i=1}^{6}y_{i})/6}{ \sum\limits_{i=1}^{6}(\ln t_{i})^{2}-(\sum\limits_{i=1}^{6}\ln t_{i})^{2}/6} \,\! }[/math]

[math]\displaystyle{ \hat{b}=\frac{-8.0699-(23.9068)(-3.0070)/6}{97.9909-(23.9068)^{2}/6} \,\! }[/math]

or:

[math]\displaystyle{ \hat{b}=1.4301 \,\! }[/math]

and:

[math]\displaystyle{ \hat{a}=\overline{y}-\hat{b}\overline{T}=\frac{\sum \limits_{i=1}^{N}y_{i}}{N}-\hat{b}\frac{\sum\limits_{i=1}^{N}\ln t_{i}}{N } \,\! }[/math]

or:

[math]\displaystyle{ \hat{a}=\frac{(-3.0070)}{6}-(1.4301)\frac{23.9068}{6}=-6.19935 \,\! }[/math]

Therefore:

[math]\displaystyle{ \hat{\beta }=\hat{b}=1.4301 \,\! }[/math]

and:

[math]\displaystyle{ \hat{\eta }=e^{-\frac{\hat{a}}{\hat{b}}}=e^{-\frac{(-6.19935)}{ 1.4301}} \,\! }[/math]

or:

[math]\displaystyle{ \hat{\eta }=76.318\text{ hr} \,\! }[/math]

The correlation coefficient can be estimated as:

[math]\displaystyle{ \hat{\rho }=0.9956 \,\! }[/math]

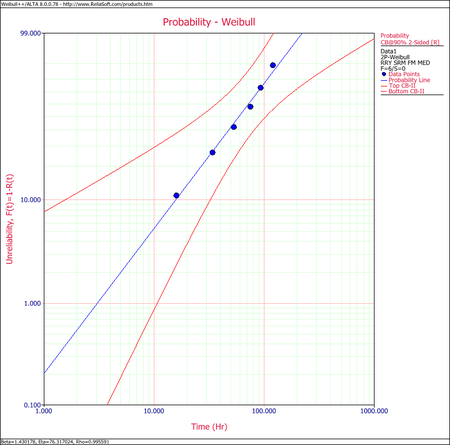
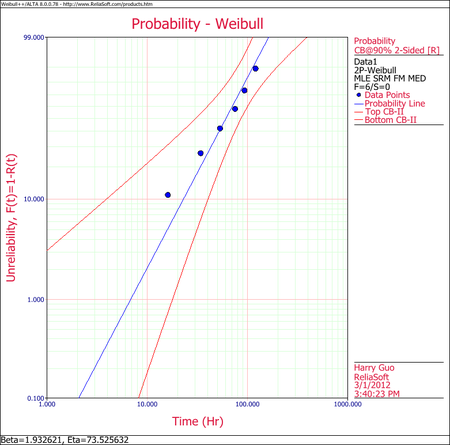
This example can be repeated in the Weibull++ software. The following plot shows the Weibull probability plot for the data set (with 90% two-sided confidence bounds).

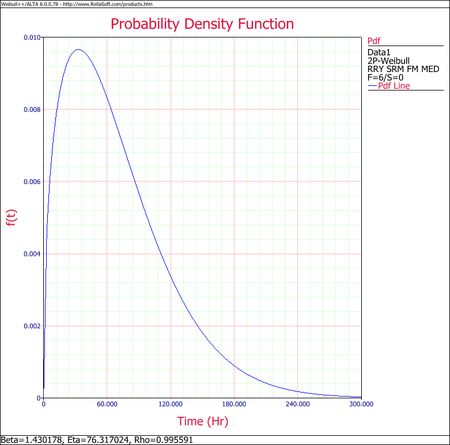
If desired, the Weibull pdf representing the data set can be written as:

[math]\displaystyle{ f(t)={\frac{\beta }{\eta }}\left( {\frac{t}{\eta }}\right) ^{\beta -1}e^{-\left( {\frac{t}{\eta }}\right) ^{\beta }} \,\! }[/math]

or:

[math]\displaystyle{ f(t)={\frac{1.4302}{76.317}}\left( {\frac{t}{76.317}}\right) ^{0.4302}e^{-\left( {\frac{t}{76.317}}\right) ^{1.4302}} \,\! }[/math]

You can also plot this result in Weibull++, as shown next. From this point on, different results, reports and plots can be obtained.

Rank Regression on X

Performing a rank regression on X is similar to the process for rank regression on Y, with the difference being that the horizontal deviations from the points to the line are minimized rather than the vertical. Again, the first task is to bring the reliability function into a linear form. This step is exactly the same as in the regression on Y analysis and all the equations apply in this case too. The derivation from the previous analysis begins on the least squares fit part, where in this case we treat as the dependent variable and as the independent variable. The best-fitting straight line to the data, for regression on X (see Parameter Estimation), is the straight line:

[math]\displaystyle{ x= \hat{a}+\hat{b}y \,\! }[/math]

The corresponding equations for [math]\displaystyle{ \hat{a} \,\! }[/math] and [math]\displaystyle{ \hat{b} \,\! }[/math] are:

[math]\displaystyle{ \hat{a}=\overline{x}-\hat{b}\overline{y}=\frac{\sum\limits_{i=1}^{N}x_{i}}{N} -\hat{b}\frac{\sum\limits_{i=1}^{N}y_{i}}{N} \,\! }[/math]

and:

[math]\displaystyle{ \hat{b}={\frac{\sum\limits_{i=1}^{N}x_{i}y_{i}-\frac{\sum \limits_{i=1}^{N}x_{i}\sum\limits_{i=1}^{N}y_{i}}{N}}{\sum \limits_{i=1}^{N}y_{i}^{2}-\frac{\left( \sum\limits_{i=1}^{N}y_{i}\right) ^{2}}{N}}} \,\! }[/math]

where:

[math]\displaystyle{ y_{i}=\ln \left\{ -\ln [1-F(t_{i})]\right\} \,\! }[/math]

and:

[math]\displaystyle{ \begin{align} x_{i}=\ln (t_{i}) \end{align}\,\! }[/math]

and the [math]\displaystyle{ F({{t}_{i}})\,\! }[/math] values are again obtained from the median ranks.

Once [math]\displaystyle{ \hat{a} \,\! }[/math] and [math]\displaystyle{ \hat{b} \,\! }[/math] are obtained, solve the linear equation for [math]\displaystyle{ y\,\! }[/math], which corresponds to:

[math]\displaystyle{ y=-\frac{\hat{a}}{\hat{b}}+\frac{1}{\hat{b}}x \,\! }[/math] Solving for the parameters from above equations, we get:

[math]\displaystyle{ a=-\frac{\hat{a}}{\hat{b}}=-\beta \ln (\eta )\,\! }[/math]

and

[math]\displaystyle{ b=\frac{1}{\hat{b}}=\beta\,\! }[/math]

The correlation coefficient is evaluated as before.

RRX Example

Again using the same data set from the probability plotting and RRY examples (with six failures at 16, 34, 53, 75, 93 and 120 hours), calculate the parameters using rank regression on X.

Solution

The same table constructed above for the RRY example can also be applied for RRX.

Using the values from this table we get:

[math]\displaystyle{ \hat{b} ={\frac{\sum\limits_{i=1}^{6}(\ln T_{i})y_{i}-\frac{ \sum\limits_{i=1}^{6}\ln T_{i}\sum\limits_{i=1}^{6}y_{i}}{6}}{ \sum\limits_{i=1}^{6}y_{i}^{2}-\frac{\left( \sum\limits_{i=1}^{6}y_{i}\right) ^{2}}{6}}} \,\! }[/math]

[math]\displaystyle{ \hat{b} =\frac{-8.0699-(23.9068)(-3.0070)/6}{7.1502-(-3.0070)^{2}/6} \,\! }[/math]

or:

[math]\displaystyle{ \hat{b}=0.6931 \,\! }[/math]

and:

[math]\displaystyle{ \hat{a}=\overline{x}-\hat{b}\overline{y}=\frac{\sum\limits_{i=1}^{6}\ln T_{i} }{6}-\hat{b}\frac{\sum\limits_{i=1}^{6}y_{i}}{6} \,\! }[/math]

or:

[math]\displaystyle{ \hat{a}=\frac{23.9068}{6}-(0.6931)\frac{(-3.0070)}{6}=4.3318 \,\! }[/math]

Therefore:

[math]\displaystyle{ \hat{\beta }=\frac{1}{\hat{b}}=\frac{1}{0.6931}=1.4428 \,\! }[/math]

and:

[math]\displaystyle{ \hat{\eta }=e^{\frac{\hat{a}}{\hat{b}}\cdot \frac{1}{\hat{ \beta }}}=e^{\frac{4.3318}{0.6931}\cdot \frac{1}{1.4428}}=76.0811\text{ hr} \,\! }[/math]

The correlation coefficient is:

[math]\displaystyle{ \hat{\rho }=0.9956 \,\! }[/math]

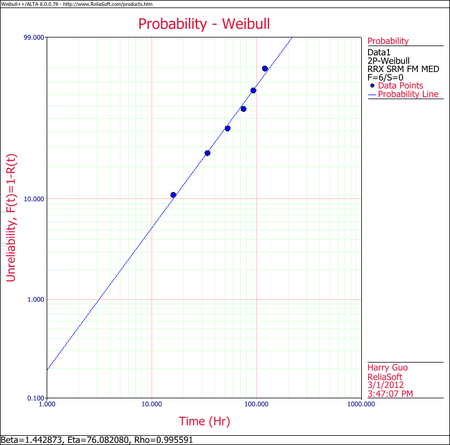
The results and the associated graph using Weibull++ are shown next. Note that the slight variation in the results is due to the number of significant figures used in the estimation of the median ranks. Weibull++ by default uses double precision accuracy when computing the median ranks.

3-Parameter Weibull Regression

When the MR versus [math]\displaystyle{ {{t}_{j}}\,\! }[/math] points plotted on the Weibull probability paper do not fall on a satisfactory straight line and the points fall on a curve, then a location parameter, [math]\displaystyle{ \gamma\,\! }[/math], might exist which may straighten out these points. The goal in this case is to fit a curve, instead of a line, through the data points using nonlinear regression. The Gauss-Newton method can be used to solve for the parameters, [math]\displaystyle{ \beta\,\! }[/math], [math]\displaystyle{ \eta\,\! }[/math] and [math]\displaystyle{ \gamma\,\! }[/math], by performing a Taylor series expansion on [math]\displaystyle{ F(t{_{i}};\beta ,\eta, \gamma )\,\! }[/math]. Then the nonlinear model is approximated with linear terms and ordinary least squares are employed to estimate the parameters. This procedure is iterated until a satisfactory solution is reached.

(Note that other shapes, particularly S shapes, might suggest the existence of more than one population. In these cases, the multiple population mixed Weibull distribution, may be more appropriate.)

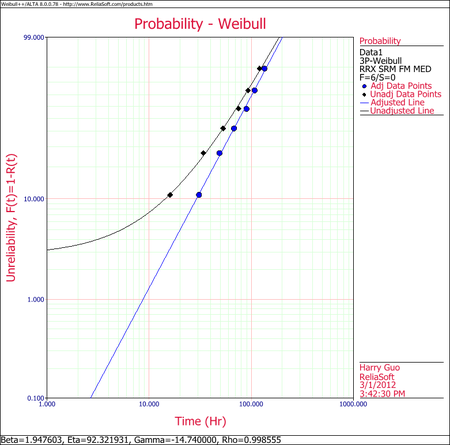
When you use the 3-parameter Weibull distribution, Weibull++ calculates the value of [math]\displaystyle{ \gamma\,\! }[/math] by utilizing an optimized Nelder-Mead algorithm and adjusts the points by this value of [math]\displaystyle{ \gamma\,\! }[/math] such that they fall on a straight line, and then plots both the adjusted and the original unadjusted points. To draw a curve through the original unadjusted points, if so desired, select Weibull 3P Line Unadjusted for Gamma from the Show Plot Line submenu under the Plot Options menu. The returned estimations of the parameters are the same when selecting RRX or RRY. To display the unadjusted data points and line along with the adjusted data points and line, select Show/Hide Items under the Plot Options menu and include the unadjusted data points and line as follows:

The results and the associated graph for the previous example using the 3-parameter Weibull case are shown next:

Maximum Likelihood Estimation

As outlined in Parameter Estimation, maximum likelihood estimation works by developing a likelihood function based on the available data and finding the values of the parameter estimates that maximize the likelihood function. This can be achieved by using iterative methods to determine the parameter estimate values that maximize the likelihood function, but this can be rather difficult and time-consuming, particularly when dealing with the three-parameter distribution. Another method of finding the parameter estimates involves taking the partial derivatives of the likelihood function with respect to the parameters, setting the resulting equations equal to zero and solving simultaneously to determine the values of the parameter estimates. ( Note that MLE asymptotic properties do not hold when estimating [math]\displaystyle{ \gamma\,\! }[/math] using MLE, as discussed in Meeker and Escobar [27].) The log-likelihood functions and associated partial derivatives used to determine maximum likelihood estimates for the Weibull distribution are covered in Appendix D.

MLE Example

One last time, use the same data set from the probability plotting, RRY and RRX examples (with six failures at 16, 34, 53, 75, 93 and 120 hours) and calculate the parameters using MLE.

Solution

In this case, we have non-grouped data with no suspensions or intervals, (i.e., complete data). The equations for the partial derivatives of the log-likelihood function are derived in an appendix and given next:

[math]\displaystyle{ \frac{\partial \Lambda }{\partial \beta }=\frac{6}{\beta } +\sum_{i=1}^{6}\ln \left( \frac{T_{i}}{\eta }\right) -\sum_{i=1}^{6}\left( \frac{T_{i}}{\eta }\right) ^{\beta }\ln \left( \frac{T_{i}}{\eta }\right) =0 \,\! }[/math]

And:

[math]\displaystyle{ \frac{\partial \Lambda }{\partial \eta }=\frac{-\beta }{\eta }\cdot 6+\frac{ \beta }{\eta }\sum\limits_{i=1}^{6}\left( \frac{T_{i}}{\eta }\right) ^{\beta }=0 \,\! }[/math]

Solving the above equations simultaneously we get:

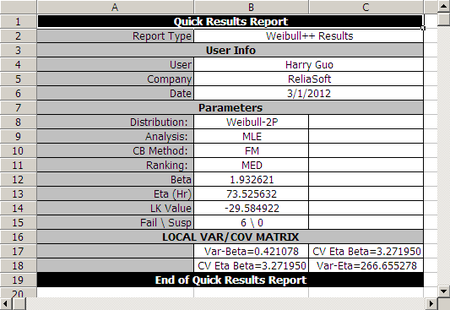
[math]\displaystyle{ \hat{\beta }=1.933,\,\! }[/math] [math]\displaystyle{ \hat{\eta }=73.526 \,\! }[/math]

The variance/covariance matrix is found to be:

[math]\displaystyle{ \left[ \begin{array}{ccc} \hat{Var}\left( \hat{\beta }\right) =0.4211 & \hat{Cov}( \hat{\beta },\hat{\eta })=3.272 \\ \hat{Cov}(\hat{\beta },\hat{\eta })=3.272 & \hat{Var} \left( \hat{\eta }\right) =266.646 \end{array} \right] \,\! }[/math]

The results and the associated plot using Weibull++ (MLE) are shown next.

You can view the variance/covariance matrix directly by clicking the Analysis Summary table in the control panel. Note that the decimal accuracy displayed and used is based on your individual Application Setup.

Unbiased MLE Beta

It is well known that the MLE [math]\displaystyle{ \beta \,\! }[/math] is biased. The biasness will affect the accuracy of reliability prediction, especially when the number of failures are small. Weibull++ provides a simple way to correct the bias of MLE [math]\displaystyle{ \beta \,\! }[/math].

When there are no right censored observations in the data, the following equation provided by Hirose [39] is used to calculated the unbiased [math]\displaystyle{ \beta \,\! }[/math].

[math]\displaystyle{ {{\beta }_{U}}=\frac{\beta }{1.0115+\frac{1.278}{r}+\frac{2.001}{{{r}^{2}}}+\frac{20.35}{{{r}^{3}}}-\frac{46.98}{{{r}^{4}}}} }[/math]

where [math]\displaystyle{ r\,\! }[/math] is the number of failures.

When there are right censored observations in the data, the following equation provided by Ross [40] is used to calculated the unbiased [math]\displaystyle{ \beta\,\! }[/math].

[math]\displaystyle{ {{\beta }_{U}}=\frac{\beta }{1+\frac{1.37}{r-1.92}\sqrt{\frac{n}{r}}} }[/math]

where [math]\displaystyle{ n\,\! }[/math] is the number of observations.

The software will use the above equations only when there are more than two failures in the data set.