Logistic Distribution Example: Difference between revisions

From ReliaWiki
Jump to navigation Jump to search
(Created page with '{| class="FCK__ShowTableBorders" border="0" cellspacing="0" cellpadding="0" align="center"; style="width:100%;" |- | valign="middle" align="left" bgcolor=EEEDF7|[[Image:Weibull-E…')
 
No edit summary
 
(12 intermediate revisions by 5 users not shown)
Line 1: Line 1:
{| class="FCK__ShowTableBorders" border="0" cellspacing="0" cellpadding="0" align="center"; style="width:100%;"
<noinclude>{{Banner Weibull Examples}}
|-
''This example appears in the [https://help.reliasoft.com/reference/life_data_analysis Life data analysis reference]''.</noinclude>
| valign="middle" align="left" bgcolor=EEEDF7|[[Image:Weibull-Examples-banner.png|400px|center]]
 
|}
The lifetime of a mechanical valve is known to follow a logistic distribution. 10 units were tested for 28 months and the following months-to-failure data were collected.
<br>The lifetime of a mechanical valve is known to follow a logistic distribution. Ten units were tested for 28 months and the following months-to-failure data was collected.
 
{| border="1" align="center" style="border-collapse: collapse;" cellpadding="5" cellspacing="5"  
|- align="center"
!Data Point Index
!State F or S
!State End Time
|- align="center"
|1 ||F || 8
|- align="center"
|2 ||F || 10
|- align="center"
|3 ||F || 15
|- align="center"
|4 ||F || 17
|- align="center"
|5 ||F || 19
|- align="center"
|6 ||F || 26
|- align="center"
|7 ||F || 27
|- align="center"
|8 ||S || 28
|- align="center"
|9 ||S || 28
|- align="center"
|10 ||S || 28
|}


<center><math>\overset{{}}{\mathop{\text{Table 10}\text{.1 - Times-to-Failure Data with Suspensions}}}\,</math></center>
<center><math>\begin{matrix}
  \text{Data Point Index} & \text{State F or S} & \text{State End Time}  \\
  \text{1} & \text{F} & \text{8}  \\
  \text{2} & \text{F} & \text{10}  \\
  \text{3} & \text{F} & \text{15}  \\
  \text{4} & \text{F} & \text{17}  \\
  \text{5} & \text{F} & \text{19}  \\
  \text{6} & \text{F} & \text{26}  \\
  \text{7} & \text{F} & \text{27}  \\
  \text{8} & \text{S} & \text{28}  \\
  \text{9} & \text{S} & \text{28}  \\
  \text{10} & \text{S} & \text{28}  \\
\end{matrix}</math></center>
    
    
:* Determine the valve's design life if specifications call for a reliability goal of 0.90.
* Determine the valve's design life if specifications call for a reliability goal of 0.90.
:* The valve is to be used in a pumping device that requires 1 month of continuous operation. What is the probability of the pump failing due to the valve?
* The valve is to be used in a pumping device that requires 1 month of continuous operation. What is the probability of the pump failing due to the valve?


This data set can be entered into Weibull++ as follows:
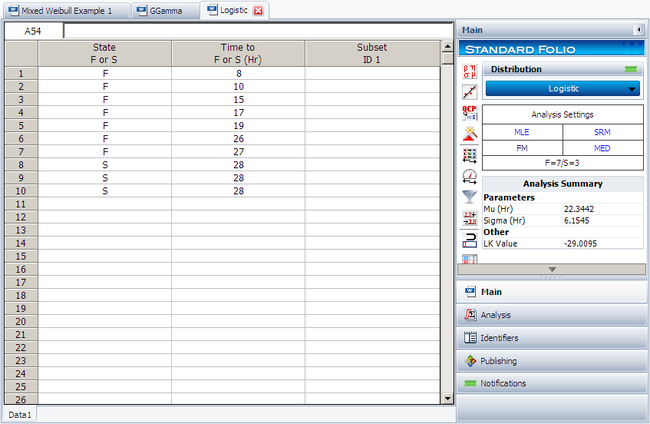
Enter the data set in a Weibull++ standard folio, as follows:


[[Image:Logistic Distribution Exmaple 1 Data.png|thumb|center|400px| ]]  
[[Image:Logistic Distribution Exmaple 1 Data.png|center|650px| ]]  


The computed parameters for maximum likelihood are:  
The computed parameters for maximum likelihood are:  
Line 32: Line 44:
   & \widehat{\mu }= & 22.34 \\  
   & \widehat{\mu }= & 22.34 \\  
  & \hat{\sigma }= & 6.15   
  & \hat{\sigma }= & 6.15   
\end{align}</math>
\end{align}\,\!</math>
 
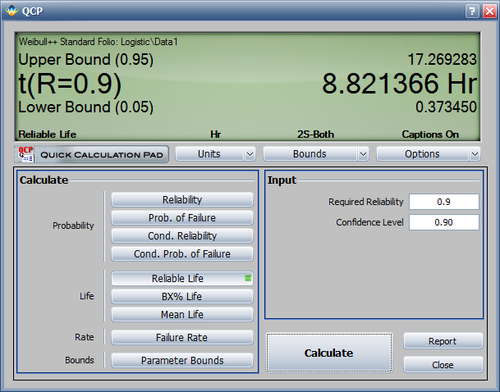
:* The valve's design life, along with 90% two sided confidence bounds, can be obtained using the QCP as follows:


[[Image:Logistic Distribution Exmaple 1 QCP Reliable Life.png|thumb|center|400px| ]]
The valve's design life, along with 90% two sided confidence bounds, can be obtained using the QCP as follows:  


:* The probability, along with 90% two sided confidence bounds, that the pump fails due to a valve failure during the first month is obtained as follows:
[[Image:Logistic Distribution Exmaple 1 QCP Reliable Life.png|center|500px| ]]


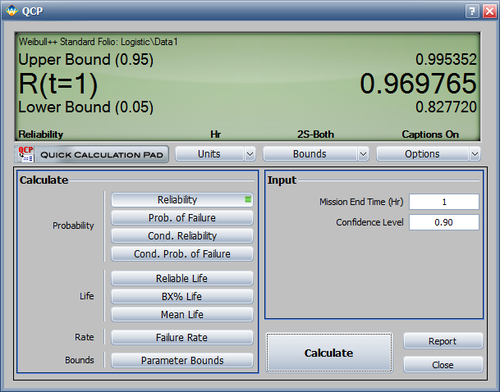
The probability, along with 90% two sided confidence bounds, that the pump fails due to a valve failure during the first month is obtained as follows:


[[Image:Logistic Distribution Exmaple 1 QCP Reliability.png|thumb|center|400px| ]]
[[Image:Logistic Distribution Exmaple 1 QCP Reliability.png|center|500px| ]]

Latest revision as of 21:39, 18 September 2023

Weibull Examples Banner.png


New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.

As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.



This example appears in the Life data analysis reference.

The lifetime of a mechanical valve is known to follow a logistic distribution. 10 units were tested for 28 months and the following months-to-failure data were collected.

Data Point Index State F or S State End Time
1 F 8
2 F 10
3 F 15
4 F 17
5 F 19
6 F 26
7 F 27
8 S 28
9 S 28
10 S 28


  • Determine the valve's design life if specifications call for a reliability goal of 0.90.
  • The valve is to be used in a pumping device that requires 1 month of continuous operation. What is the probability of the pump failing due to the valve?

Enter the data set in a Weibull++ standard folio, as follows:

Logistic Distribution Exmaple 1 Data.png

The computed parameters for maximum likelihood are:

[math]\displaystyle{ \begin{align} & \widehat{\mu }= & 22.34 \\ & \hat{\sigma }= & 6.15 \end{align}\,\! }[/math]

The valve's design life, along with 90% two sided confidence bounds, can be obtained using the QCP as follows:

Logistic Distribution Exmaple 1 QCP Reliable Life.png

The probability, along with 90% two sided confidence bounds, that the pump fails due to a valve failure during the first month is obtained as follows:

Logistic Distribution Exmaple 1 QCP Reliability.png
Retrieved from "https://www.reliawiki.com/index.php?title=Logistic_Distribution_Example&oldid=66166"