Degradation Data Analysis: Difference between revisions
Kate Racaza (talk | contribs) (updated example 2) |
|||
| Line 13: | Line 13: | ||
::<math>\begin{matrix} | |||
Linear\ \ & y=a\cdot x+b \\ | Linear\ \ & y=a\cdot x+b \\ | ||
Exponential & y=b\cdot {{e}^{a\cdot x}} \\ | Exponential & y=b\cdot {{e}^{a\cdot x}} \\ | ||
| Line 20: | Line 20: | ||
Gompertz & y=a\cdot {{b}^{{{c}^{x}}}} \\ | Gompertz & y=a\cdot {{b}^{{{c}^{x}}}} \\ | ||
Lloyd-Lipow & y=a-\frac{b}{x} \\ | Lloyd-Lipow & y=a-\frac{b}{x} \\ | ||
\end{matrix}</math> | \end{matrix}</math> | ||
where <math>y</math> represents the performance, <math>x</math> represents time, and <math>a,</math> <math>b</math> and <math>c</math> are model parameters to be solved for. | where <math>y</math> represents the performance, <math>x</math> represents time, and <math>a,</math> <math>b</math> and <math>c</math> are model parameters to be solved for. | ||
| Line 32: | Line 31: | ||
Five turbine blades are tested for crack propagation. The test units are cyclically stressed and inspected every 100,000 cycles for crack length. Failure is defined as a crack of length 30mm or greater. The following table shows the test results for the five units at each cycle: | Five turbine blades are tested for crack propagation. The test units are cyclically stressed and inspected every 100,000 cycles for crack length. Failure is defined as a crack of length 30mm or greater. The following table shows the test results for the five units at each cycle: | ||
::<math>\begin{matrix} | |||
Cycles (x1000) & Unit A (mm)& Unit B (mm) & Unit C (mm) & Unit D (mm)& Unit E (mm) \\ | Cycles (x1000) & Unit A (mm)& Unit B (mm) & Unit C (mm) & Unit D (mm)& Unit E (mm) \\ | ||
100 & 15 & 10 & 17 & 12 & 10 \\ | 100 & 15 & 10 & 17 & 12 & 10 \\ | ||
| Line 40: | Line 38: | ||
400 & 26 &25 & 27 & 20 & 26 \\ | 400 & 26 &25 & 27 & 20 & 26 \\ | ||
500 & 29 & 30 & 33 &26 & 33 \\ | 500 & 29 & 30 & 33 &26 & 33 \\ | ||
\end{matrix}</math> | \end{matrix}</math> | ||
Use the exponential degradation model to extrapolate the times-to-failure data. | Use the exponential degradation model to extrapolate the times-to-failure data. | ||
'''Solution''' | '''Solution''' | ||
| Line 50: | Line 46: | ||
The first step is to solve the equation <math>y=b\cdot {{e}^{a\cdot x}}</math> for <math>a</math> and <math>b</math> for each of the test units. Using regression analysis, the values for each of the test units are: | The first step is to solve the equation <math>y=b\cdot {{e}^{a\cdot x}}</math> for <math>a</math> and <math>b</math> for each of the test units. Using regression analysis, the values for each of the test units are: | ||
::<math>\begin{matrix} | |||
{} & a & b \\ | {} & a & b \\ | ||
Unit A & 0.00158 & 13.596 \\ | Unit A & 0.00158 & 13.596 \\ | ||
| Line 57: | Line 53: | ||
Unit D & 0.00177 & 10.361 \\ | Unit D & 0.00177 & 10.361 \\ | ||
Unit E & 0.00294 & 7.931 \\ | Unit E & 0.00294 & 7.931 \\ | ||
\end{matrix}</math> | \end{matrix}</math> | ||
Substituted the values into the underlying exponential model, solved for <math>x</math> or: | Substituted the values into the underlying exponential model, solved for <math>x</math> or: | ||
::<math>x=\frac{\text{ln}(y)-\text{ln}(b)}{a}</math> | ::<math>x=\frac{\text{ln}(y)-\text{ln}(b)}{a}</math> | ||
Using the values of <math>a</math> and <math>b</math> , with <math>y=30</math> , the resulting time at which the crack length reaches 30mm can then found for each sample: | Using the values of <math>a</math> and <math>b</math> , with <math>y=30</math> , the resulting time at which the crack length reaches 30mm can then found for each sample: | ||
::<math>\begin{matrix} | |||
{} & Cycles-to-Failure \\ | {} & Cycles-to-Failure \\ | ||
Unit A & \text{500,622} \\ | Unit A & \text{500,622} \\ | ||
| Line 75: | Line 68: | ||
Unit D & \text{600,810} \\ | Unit D & \text{600,810} \\ | ||
Unit E & \text{452,832} \\ | Unit E & \text{452,832} \\ | ||
\end{matrix}</math | \end{matrix}</math> | ||
Revision as of 04:00, 6 August 2012
Introduction
Given that products are more frequently being designed with higher reliability and developed in a shorter amount of time, it is often not possible to test new designs to failure under normal operating conditions. In some cases, it is possible to infer the reliability behavior of unfailed test samples with only the accumulated test time information and assumptions about the distribution. However, this generally leads to a great deal of uncertainty in the results. Another option in this situation is the use of degradation analysis. Degradation analysis involves the measurement of performance data that can be directly related to the presumed failure of the product in question. Many failure mechanisms can be directly linked to the degradation of part of the product, and degradation analysis allows the analyst to extrapolate to an assumed failure time based on the measurements of degradation over time.
In some cases, it is possible to directly measure the degradation over time, as with the wear of brake pads or with the propagation of crack size. In other cases, direct measurement of degradation might not be possible without invasive or destructive measurement techniques that would directly affect the subsequent performance of the product. In such cases, the degradation of the product can be estimated through the measurement of certain performance characteristics, such as using resistance to gauge the degradation of a dielectric material. In either case, however, it is necessary to be able to define a level of degradation or performance at which a failure is said to have occurred. With this failure level defined, it is a relatively simple matter to use basic mathematical models to extrapolate the measurements over time to the point where the failure is said to occur. Once these have been determined, it is merely a matter of analyzing the extrapolated failure times in the same manner as conventional time-to-failure data.
Once the level of failure (or the degradation level that would constitute a failure) is defined, the degradation for multiple units over time needs to be measured. As with conventional reliability data, the amount of certainty in the results is directly related to the number of units being tested. The degradation of these units needs to be measured over time, either continuously or at predetermined intervals.
Degradation Models
Once the degradation information has been recorded, the next task is to extrapolate the measurements to the defined failure level in order to estimate the failure time. Weibull++ allows the user to perform such extrapolation using a linear, exponential, power or logarithmic model. These models have the following forms:
- [math]\displaystyle{ \begin{matrix} Linear\ \ & y=a\cdot x+b \\ Exponential & y=b\cdot {{e}^{a\cdot x}} \\ Power & y=b\cdot {{x}^{a}} \\ Logarithmic & y=a\cdot ln(x)+b \\ Gompertz & y=a\cdot {{b}^{{{c}^{x}}}} \\ Lloyd-Lipow & y=a-\frac{b}{x} \\ \end{matrix} }[/math]
where [math]\displaystyle{ y }[/math] represents the performance, [math]\displaystyle{ x }[/math] represents time, and [math]\displaystyle{ a, }[/math] [math]\displaystyle{ b }[/math] and [math]\displaystyle{ c }[/math] are model parameters to be solved for.
Once the model parameters [math]\displaystyle{ {{a}_{i}} }[/math] , [math]\displaystyle{ {{b}_{i}} }[/math] and [math]\displaystyle{ {{c}_{i}} }[/math] are estimated for each sample [math]\displaystyle{ i }[/math] , a time, [math]\displaystyle{ {{x}_{i}} }[/math] , can be extrapolated, which corresponds to the defined level of failure [math]\displaystyle{ y }[/math] . The computed [math]\displaystyle{ {{x}_{i}} }[/math] values can now be used as our times-to-failure for subsequent life data analysis. As with any sort of extrapolation, one must be careful not to extrapolate too far beyond the actual range of data in order to avoid large inaccuracies (modeling errors).
Example 1: Crack Propagation Example (Point Estimation)
Five turbine blades are tested for crack propagation. The test units are cyclically stressed and inspected every 100,000 cycles for crack length. Failure is defined as a crack of length 30mm or greater. The following table shows the test results for the five units at each cycle:
- [math]\displaystyle{ \begin{matrix} Cycles (x1000) & Unit A (mm)& Unit B (mm) & Unit C (mm) & Unit D (mm)& Unit E (mm) \\ 100 & 15 & 10 & 17 & 12 & 10 \\ 200 & 20& 15 & 25 & 16 & 15 \\ 300 & 22 & 20 &26 & 17 & 20 \\ 400 & 26 &25 & 27 & 20 & 26 \\ 500 & 29 & 30 & 33 &26 & 33 \\ \end{matrix} }[/math]
Use the exponential degradation model to extrapolate the times-to-failure data.
Solution
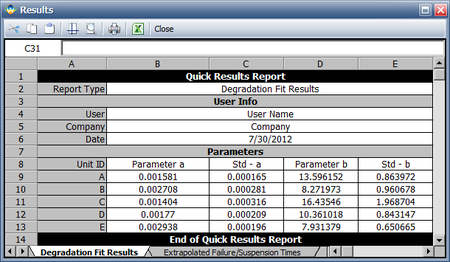
The first step is to solve the equation [math]\displaystyle{ y=b\cdot {{e}^{a\cdot x}} }[/math] for [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] for each of the test units. Using regression analysis, the values for each of the test units are:
- [math]\displaystyle{ \begin{matrix} {} & a & b \\ Unit A & 0.00158 & 13.596 \\ Unit B & 0.00271 & 8.272 \\ Unit C & 0.00140 & 16.435 \\ Unit D & 0.00177 & 10.361 \\ Unit E & 0.00294 & 7.931 \\ \end{matrix} }[/math]
Substituted the values into the underlying exponential model, solved for [math]\displaystyle{ x }[/math] or:
- [math]\displaystyle{ x=\frac{\text{ln}(y)-\text{ln}(b)}{a} }[/math]
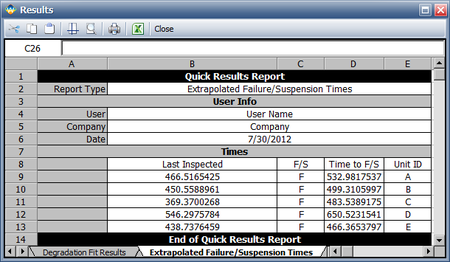
Using the values of [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] , with [math]\displaystyle{ y=30 }[/math] , the resulting time at which the crack length reaches 30mm can then found for each sample:
- [math]\displaystyle{ \begin{matrix} {} & Cycles-to-Failure \\ Unit A & \text{500,622} \\ Unit B & \text{475,739} \\ Unit C & \text{428,739} \\ Unit D & \text{600,810} \\ Unit E & \text{452,832} \\ \end{matrix} }[/math]
These times-to-failure can now be analyzed using traditional life data analysis to obtain metrics such as the probability of failure, B10 life, mean life, etc. This analysis can be automatically performed in the Weibull++ degradation analysis folio. View the Weibull++ solution in HTML or Video
Using Extrapolated Intervals
The parameters in a degradation model are estimated using available degradation data. If the data is large, the uncertainty of the estimated parameters will be small. Otherwise, the uncertainty will be large. Since the failure time for a test unit is predicted based on the estimated model, we sometimes would like to see how the parameter uncertainty affects the failure time prediction. Let’s use the exponential model as an example. Assume the critical degradation value is [math]\displaystyle{ {{y}_{crit}} }[/math]. The predicted failure time will be:
The variance of the predicted failure time will be:
The variance and covariance of the model parameters are calculated from using Least Squares Estimation. The details of the calculation are not given here.
The 2-sided upper and lower bounds for the predicted failure time, with a confidence level of [math]\displaystyle{ 1-\alpha }[/math] are:
In Weibull++, the default confidence level is 90%.
Example 2: Crack Propagation Example (Extrapolated Intervals)
Using the same data in example 1, predict the interval failure times for the turbine blades.
Solution
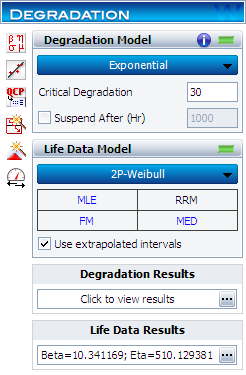
In the Weibull++ degradation analysis folio, select the Use extrapolated intervals check box, as shown next.
Use the exponential degradation model for the degradation analysis, and the Weibull distribution parameters with MLE for the life data analysis. The following report shows the estimated degradation model parameters.
The following report shows the extrapolated failure time intervals.