General Examples & Case Studies
In this chapter we present some application examples utilizing ReliaSoft's ALTA. We assume that you have previously consulted the ALTA User's Guide and familiarized yourself with the software.
Arrhenius
A mechanical component was put into an accelerated life test with temperature as the stress type. The objective is to fit the Arrhenius-Weibull model to the observed data and analyze the result of the test. The following times-to-failure data were observed.
| 343 K | 363 K | 383 K |
|---|---|---|
| 266.66 | 618.54 | 351.12 |
| 430.09 | 666.72 | 355.1 |
| 570.45 | 724.4 | 672.69 |
| 890.42 | 950.89 | 923.35 |
| 1046.65 | 1148.4 | 948.22 |
| 1158.14 | 1202.94 | 1277.04 |
| 1396.01 | 1492.56 | 1538.81 |
| 1918.38 | 1619.59 | 2020.34 |
| 2028.86 | 2592.29 | 2099.03 |
| 2785.58 | 3596.85 | 2173.04 |
The parameters of the Arrhenius-Weibull model were estimated using the ALTA standard folio. The results are:
- [math]\displaystyle{ \begin{align} \beta =1.771460,\text{ }B=86.183591,\text{ }C=1170.423770. \end{align} }[/math]
The estimate shows a small value for [math]\displaystyle{ \beta }[/math]. The following observations can then be made:
- Life is not accelerated with temperature, or
- The stress increments were not sufficient, or
- The stress values used in the test were well within the "specification limits" for the product (see discussion here).
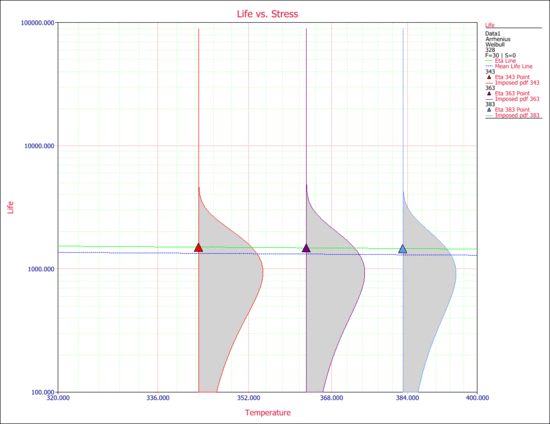
The value of [math]\displaystyle{ \beta }[/math] is not the only indicator for the observed behavior. As you can see from the data obtained from the test, the times-to-failure at all three stress levels fall within the same ranges. Another way to observe this is by looking at the Life vs. Stress plot. The following plot shows the scale parameter, [math]\displaystyle{ \eta }[/math], and the mean life. As you can see, the life ( [math]\displaystyle{ \eta }[/math] and the mean life) are almost invariant with stress.
27 circuit boards were put in an accelerated life test, with temperature as the stress (or stimuli). The goal is to estimate the reliability of the circuit boards after 10 years when operating at 100ºC. The following data were obtained:
| Test Chamber Temperature 463K | ||
|---|---|---|
| # of units | Time, hr | Observation |
| 1 | 2,403 | Failure |
| 1 | 2,668 | Unrelated Failure |
| 1 | 3,669 | Test Fixture Failure |
| 1 | 3,863 | Failure |
| 2 | 4,400 | Test Fixture Failure |
| 2 | 4,767 | Failure |
| 1 | 5,219 | Failure |
| 4 | 5,276 | Power Surge Failure |
| 2 | 7,517 | Failure |
| 1 | 7,840 | Failure |
| 2 | 8,025 | Failure |
| 1 | 8,571 | Removed - Test Terminated |
| Test Chamber Temperature 488K | ||
|---|---|---|
| # of units | Time, hr | Observation |
| 2 | 346 | Power Regulator Failure |
| 1 | 1,416 | Failure |
| 1 | 2,197 | Unrelated Failure |
| 1 | 2,533 | Failure |
| 1 | 2,630 | Failure |
| 1 | 2,701 | Test Fixture Failure |
| 1 | 3,000 | Failure |
| 1 | 3,489 | Failure |
| 1 | 6,720 | Removed - Test Terminated |
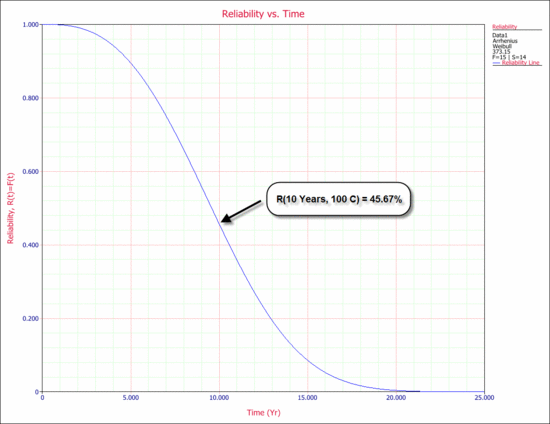
The data were entered in the ALTA standard folio and analyzed with the Arrhenius-Weibull model. Note that all units that did not fail in the test, but failed for unrelated reasons, were entered as suspensions. The reliability after 10 years at 100ºC is estimated to be 45.67%, as shown in the following reliability plot. This reliability value can also be obtained via the Quick Calculation Pad (QCP).
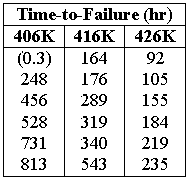
An electronic component was redesigned and then tested to failure at three different temperatures. Six units were tested at each temperature level. At the 406 K stress level, however, a unit was removed from the test due to a test equipment failure which led to a failure of the component. A warranty time of one year is to be given, with an expected return of 10% of the population. The following table shows the times-to-failure and test temperatures.
The operating temperature is 356 K. Using the Arrhenius-Weibull model, determine the following:
1) Should the first failure at 406 K be included in the analysis?
2) Determine the warranty time for a 90% reliability.
3) Determine the 90% lower confidence limit on the warranty time.
4) Is the warranty requirement met? If not, what steps should be taken?
5) Repeat the analysis with the unrelated failure included. Is there any difference?
6) If the unrelated failure occurred at 500 hr, should it be included in the analysis?
Solution
1) Since the failure occurred at the very beginning of the test and for an unrelated reason, it can be omitted from the analysis. If it is included it should be treated as a suspension and not as a failure.
2) Disregard the first failure at 406 K and analyze the data using the ALTA standard folio. The estimated parameters are:
- [math]\displaystyle{ \begin{align} \beta =\ & 2.965820 \\ B=\ & 10679.567542 \\ C=\ & 2.396615\cdot {{10}^{-9}} \end{align} }[/math]
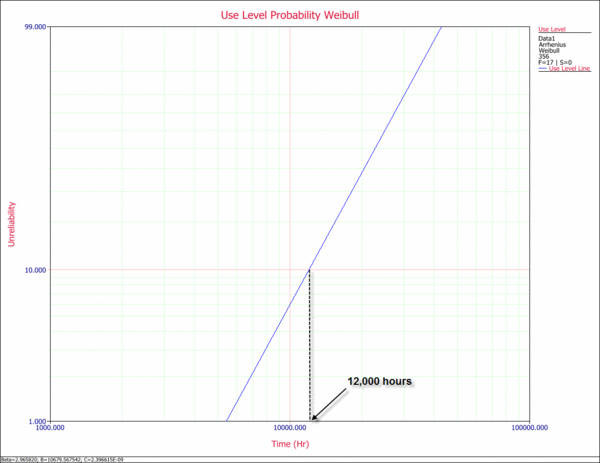
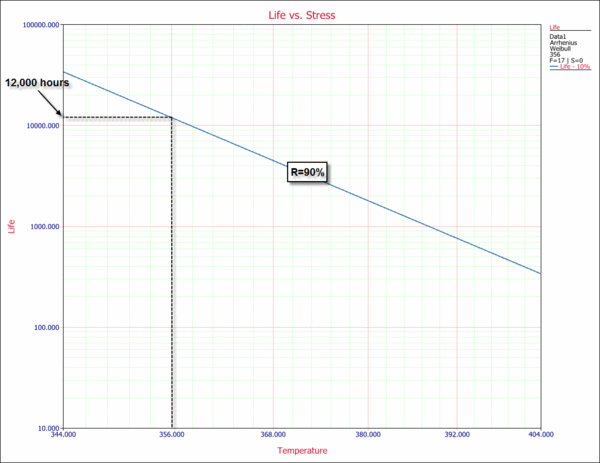
The following plot shows the use level probability plot of the analysis. The warranty time for a reliability of 90% (or an unreliability of 10%) can be estimated from this plot, as shown next.
This estimate can also be obtained from the Arrhenius plot (Life vs. Stress plot). The 10th percentile (time for a reliability of 90%) is plotted versus stress. This type of plot is useful because it allows you to determine a time for a given reliability for different stress levels.
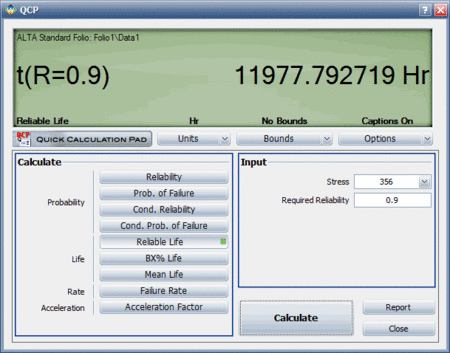
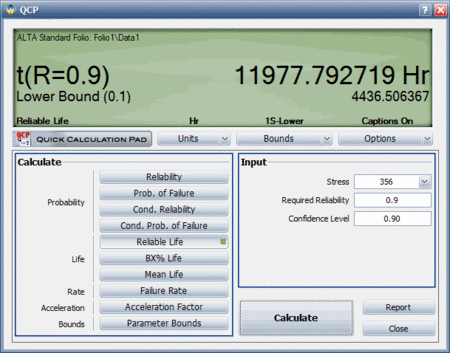
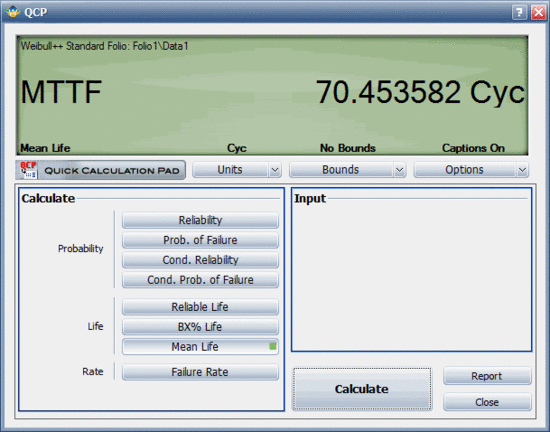
A more accurate way to determine the warranty time would be to use ALTA's Quick Calculation Pad (QCP), which estimates the reliable life to be 11,977.792719 hours, as shown next:
3) From the use level probability plot, the warranty time for a 90% reliability was estimated to be approximately 12,000 hours. This is above the 1 year (8,760 hours) requirement. However, this is an estimate at the 50% confidence level. In other words, 50% of the time life will be greater than 12,000 hours and 50% of the time life will be less. A known confidence level is therefore crucial before any decisions are made.
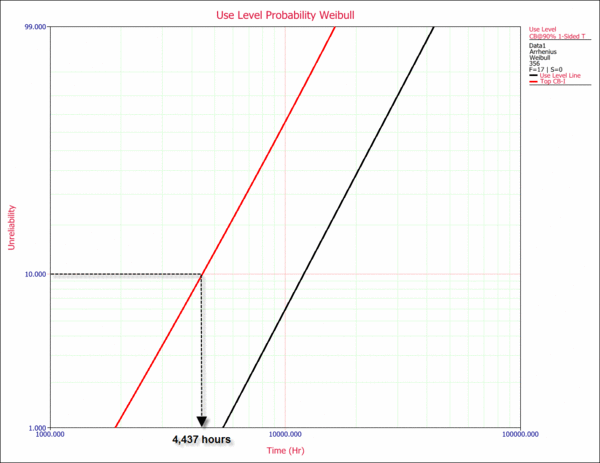
Plot the confidence bounds on both probability and Arrhenius plots. The following use level probability plot, shows the 90% lower confidence level (LCL). Note that in ALTA, percentile bounds are Type 1 confidence bounds.
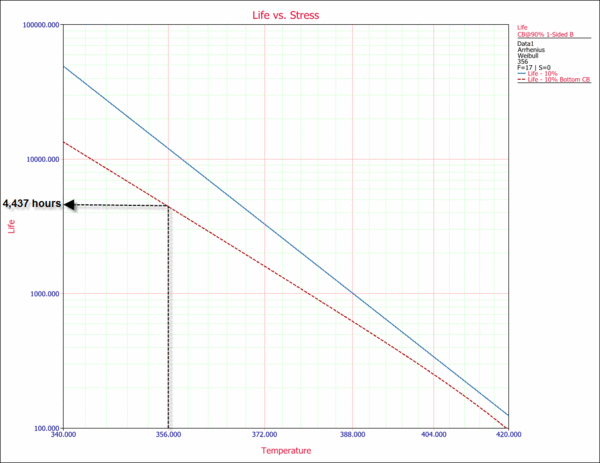
From the plot, we obtain an estimate of 4,437 hr warranty time at a 90% lower confidence level. This means that 90% of the time, life will be greater than this value. In other words, a life of 4,437 hr is a bounding value for the warranty. The Arrhenius plot with the 90% lower confidence level is shown next.
You can use the QCP to calculate calculate the lower confidence bound. The result shows a lower bound of 4,436.506367 hours.
4) The warranty time for this component is estimated to be 4,436.5 hours at a 90% lower confidence bound. This is much less than the 1 year warranty time required (almost 6 months). Thus the desired warranty is not met. In this case, the following four options are available:
- a) Redesign.
- b) Reduce the confidence level.
- c) Change the warranty policy.
- d) Test additional units at stress levels closer to the use level.
5) Including the unrelated failure of 0.3 hours at 406 K (by treating it as a suspension) in the analysis obtains the following results:
- [math]\displaystyle{ \begin{align} \beta =\ & 2.965804 \\ B=\ & 10679.566625 \\ C=\ & 2.396619\cdot {{10}^{-9}} \end{align} }[/math]
These results are essentially identical to the results obtained when the unrelated failure was excluded. A small difference can be seen only if more significant digits are considered. The warranty time with the 90% lower 1-sided confidence bound is estimated to be:
- [math]\displaystyle{ \begin{align} T=\ & 11977.729145\text{ hr} \\ {{T}_{L}}=\ & 4436.462084\text{ hr} \end{align} }[/math]
Again, the difference is negligible. This is due to the very early time at which this unrelated failure occurred.
6) Repeat the analysis treating the unrelated failure at 500 hours as a suspension. The results are:
- [math]\displaystyle{ \begin{align} \beta =\ & 3.022714 \\ B=\ & 10959.523204 \\ C=\ & 1.23808\cdot {{10}^{-9}} \end{align} }[/math]
In this case, the results are very different. The warranty time with the 90% lower 1-sided confidence bound is estimated to be:
- [math]\displaystyle{ \begin{align} T=\ & 13780.208409\text{ hr} \\ {{T}_{L}}=\ & 5303.672050\text{ hr} \end{align} }[/math]
As you can see, it would be a mistake to neglect the unrelated failure in this case. By neglecting this failure, we would actually underestimate the warranty time. The important observation in this example is that every piece of life information is crucial. In other words, unrelated failures also provide information about the life of the product. An unrelated failure occurring at 500 hours indicates that the product has survived for that period of time under the particular stress level; thus, neglecting it would be a mistake. On the other hand, it would also be a mistake to treat this data point as a failure, since the failure was caused by the faulty test equipment.
100 units of an electronic device are tested using two test chambers. Each test chamber contains 50 units and is set to a different temperature. The test is performed continuously for 15 weeks, but monitored only on a weekly basis; therefore, the exact times at which the units failed are unknown. For each failed unit, the only information available is whether or not it failed between inspections.
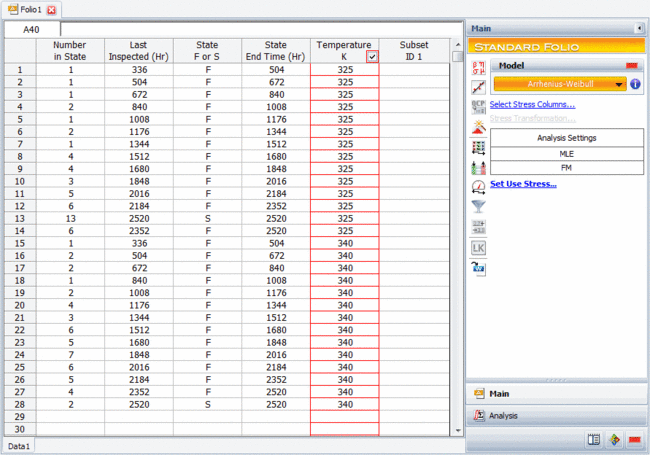
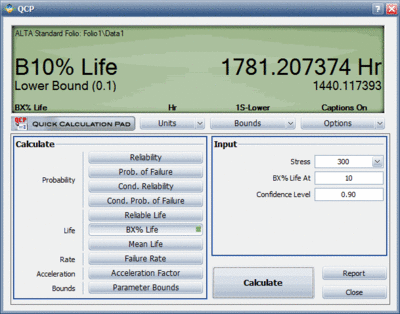
The goal of the test is to estimate the 90% lower bound on the [math]\displaystyle{ B10 }[/math] life (in hours) of the electronic device. The data obtained from the test are recorded in an ALTA standard folio, using the interval data format, as shown next. The normal use condition is assumed to be 300K.
Assuming that the failure times of the device follow a Weibull distribution and that the Arrhenius model is an adequate life-stress relationship, we obtain the following estimates for the parameters:
- [math]\displaystyle{ \begin{align} \beta =\ & 3.425937 \\ B=\ & 1488.412639 \\ C=\ & 24.059577 \end{align} }[/math]
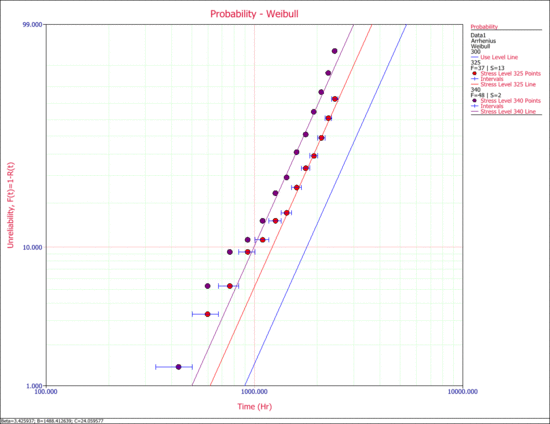
The next figure show the probability lines at the different stress levels, along with the extrapolated use level probability line.
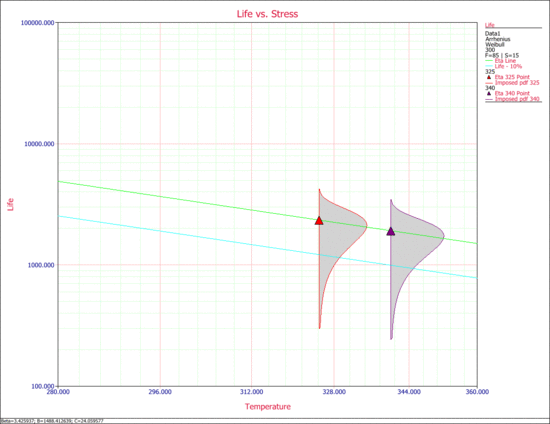
The following Life vs. Stress plot shows the [math]\displaystyle{ B10 }[/math] life line.
The 90% lower bound on the [math]\displaystyle{ B10 }[/math] life can be estimated as follows.
Inverse Power Law
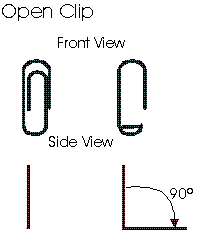
To illustrate the principles behind accelerated testing, consider the following simple example which involves a paper clip. The objective is to determine the mean number of cycles-to-failure of the paper clip. Assume that the use cycle is a 45º bend. The acceleration stress is determined to be the angle to which the paper clip is bent. In this case, assume that the two accelerated bend stresses are 90º and 180º. For the 90º bend, test the paper clip using the following procedure. Use a similar procedure for the 180º and 45º tests.
Note that the paper clips used in this example are Jumbo paper clips that are capable of repeated bending. Different paper clips will yield different results. Additionally, and so that no other stresses are imposed, take caution to assure that the rate at which the paper clips are cycled remains the same across the experiment.
Paper Clip Test
1) Open the Paper Clip.
- a. With one hand, hold the clip by the longer, outer loop.
- b. With the thumb and forefinger of the other hand, grasp the smaller, inner loop.
- c. Pull the smaller, inner loop out and down 90º so that a right angle is formed as shown.
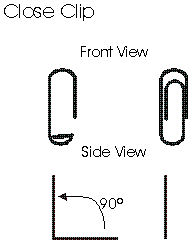
2) Close the Paper Clip.
- a. With one hand, continue to hold the clip by the longer, outer loop.
- b. With the thumb and forefinger of the other hand, grasp the smaller, inner loop.
- c. Push the smaller inner loop up and in 90º so that the smaller loop is returned to the original upright position in line with the larger, outer loop as shown.
This completes one cycle.
3) Repeat steps 1 and 2 until the paper clip breaks. Count and record the cycles-to-failure for each clip.
Analysis
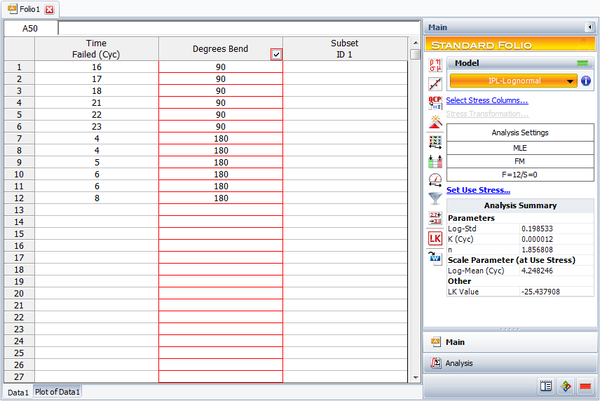
In this experiment, a sample of six paper clips were tested to failure at both 90º and 180º bends. A base test sample of six paper clips was tested at a 45º bend (the assumed use stress level) to confirm the analysis. The cycles-to-failure are given next.
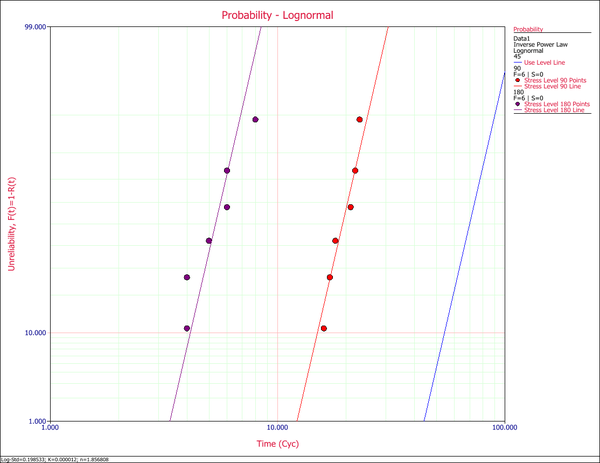
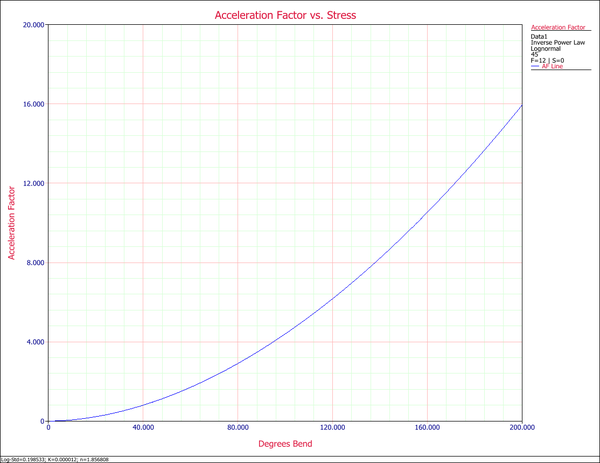
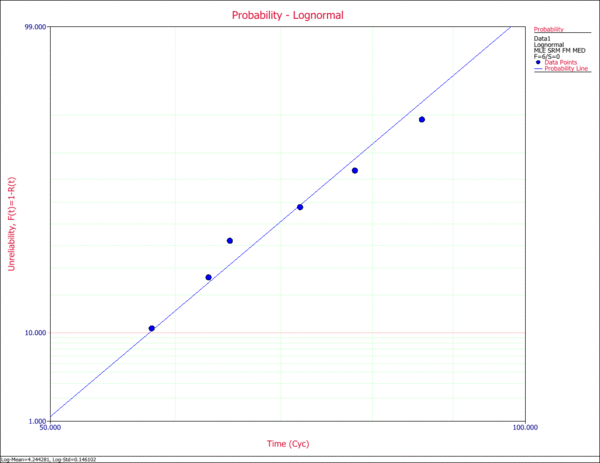
Enter the data in an ALTA standard folio, and analyze the results assuming a lognormal life distribution (fatigue) and an inverse power law relationship (non-thermal) for the life-stress model. The following figures show the analysis and some of the results.
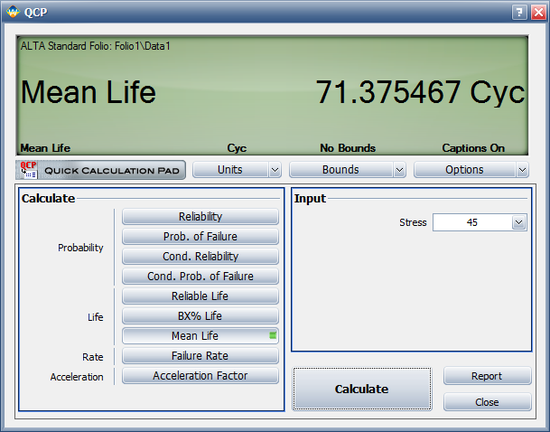
The MTTF at 45º is estimated to be 71.375467 cycles, as shown next.
The next two figures show the analysis of the base data in Weibull++ and the base MTTF estimate. In this case, our accelerated test correctly predicted the MTTF as verified by our base test.
A tensile component of a landing gear is put through an accelerated reliability test to determine whether the life goal would be achieved under the designed-in load. Fifteen units, N=15, are tested at three different shock loads. The component is designed for a peak shock load of 50 kips with an estimated return of 10% of the population by 10,000 cycles (or landings). Using the Inverse Power Law-Lognormal model, determine whether the design life is met.
The following table shows the data from the test.
| Failure, in Cycles | Shock Load, kips |
|---|---|
| 1855 | 73 |
| 2158 | 73 |
| 2425 | 73 |
| 2736 | 73 |
| 3206 | 73 |
| 614 | 95 |
| 770 | 95 |
| 781 | 95 |
| 890 | 95 |
| 1055 | 95 |
| 152 | 128 |
| 162 | 128 |
| 173 | 128 |
| 209 | 128 |
| 216 | 128 |
The data are entered into the ALTA standard folio, and the following parameters for the IPL-lognormal model are obtained:
- [math]\displaystyle{ \begin{align} Std=\ & 0.179080 \\ K=\ & 8.953055E-13 \\ n=\ & 4.638882 \end{align} }[/math]
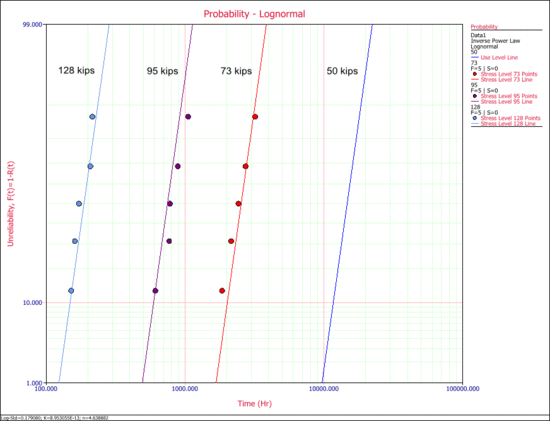
The following probability plot shows the plot at each test stress level (73 kips, 95 kips and 128 kips) and at the use stress level (50 kips). As you can see, there is a good agreement between the data and the fitted model.
The probability plot can be used to estimate the cycles-to failure for a 10% unreliability probability of failure. According to the plot, the cycles-to-failure is estimated to be [math]\displaystyle{ T(Q=0.10=10%)\approxeq 12,000 }[/math] landings. (By pressing SHIFT and clicking the plot, you can display the coordinates and read the value on the X axis that corresponds to a value of 10 in the Y axis.)
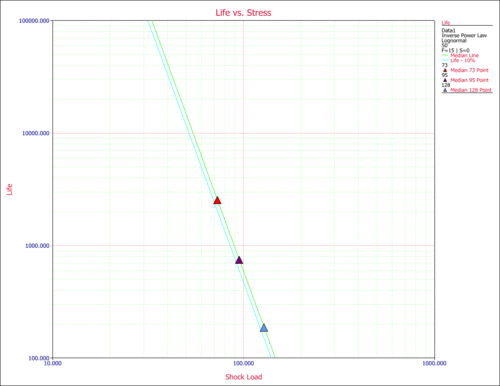
Another way to obtain life information is to use the Life vs. Stress plot to plot the life line that corresponds to the 10% unreliability. The following plot shows the life line for the 10% unreliability (the first line from the left). For a stress of 50 kips (X-axis) and for the 10% unreliability line, the cycles-to-failure can be obtained by reading the value on the Y-axis. Again, [math]\displaystyle{ T(0.1)\approxeq 12,000 }[/math] landings.
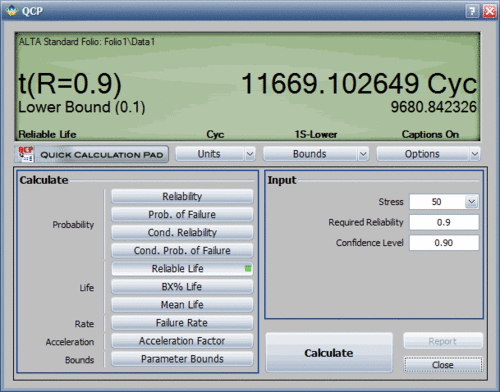
However, a more accurate way to obtain the information is to use the Quick Calculation Pad (QCP) in ALTA. Using the QCP, the life for a 10% probability of failure at 50 kips is estimated to be 11,669.1 landings. This is very close to the requirement. In addition, this estimate was obtained at the 50% confidence level. In other words, 50% of the time life will be greater than 11,669.1 landings, and 50% of the time life will be less. Thus, we need to obtain an estimate of the lower confidence level before any decisions are made. The following figure shows the QCP calculation that includes a 90% lower 1-sided confidence bound on the estimate. The lower confidence bound is estimated to be 9,680.84 landings. Thus, the 10,000 landings criterion is not quite met.
A tensile component of a landing gear is put through an accelerated reliability test to determine whether the life goal would be achieved under the designed-in load. Fifteen units, N=15, are tested at three different shock loads. The component is designed for a peak shock load of 50 kips with an estimated return of 10% of the population by 10,000 cycles (or landings). Using the Inverse Power Law-Lognormal model, determine whether the design life is met.
The following table shows the data from the test.
| Failure, in Cycles | Shock Load, kips |
|---|---|
| 1855 | 73 |
| 2158 | 73 |
| 2425 | 73 |
| 2736 | 73 |
| 3206 | 73 |
| 614 | 95 |
| 770 | 95 |
| 781 | 95 |
| 890 | 95 |
| 1055 | 95 |
| 152 | 128 |
| 162 | 128 |
| 173 | 128 |
| 209 | 128 |
| 216 | 128 |
The data are entered into the ALTA standard folio, and the following parameters for the IPL-lognormal model are obtained:
- [math]\displaystyle{ \begin{align} Std=\ & 0.179080 \\ K=\ & 8.953055E-13 \\ n=\ & 4.638882 \end{align} }[/math]
The following probability plot shows the plot at each test stress level (73 kips, 95 kips and 128 kips) and at the use stress level (50 kips). As you can see, there is a good agreement between the data and the fitted model.
The probability plot can be used to estimate the cycles-to failure for a 10% unreliability probability of failure. According to the plot, the cycles-to-failure is estimated to be [math]\displaystyle{ T(Q=0.10=10%)\approxeq 12,000 }[/math] landings. (By pressing SHIFT and clicking the plot, you can display the coordinates and read the value on the X axis that corresponds to a value of 10 in the Y axis.)
Another way to obtain life information is to use the Life vs. Stress plot to plot the life line that corresponds to the 10% unreliability. The following plot shows the life line for the 10% unreliability (the first line from the left). For a stress of 50 kips (X-axis) and for the 10% unreliability line, the cycles-to-failure can be obtained by reading the value on the Y-axis. Again, [math]\displaystyle{ T(0.1)\approxeq 12,000 }[/math] landings.
However, a more accurate way to obtain the information is to use the Quick Calculation Pad (QCP) in ALTA. Using the QCP, the life for a 10% probability of failure at 50 kips is estimated to be 11,669.1 landings. This is very close to the requirement. In addition, this estimate was obtained at the 50% confidence level. In other words, 50% of the time life will be greater than 11,669.1 landings, and 50% of the time life will be less. Thus, we need to obtain an estimate of the lower confidence level before any decisions are made. The following figure shows the QCP calculation that includes a 90% lower 1-sided confidence bound on the estimate. The lower confidence bound is estimated to be 9,680.84 landings. Thus, the 10,000 landings criterion is not quite met.
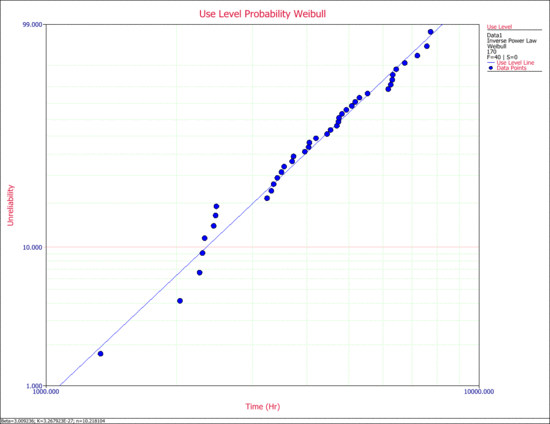
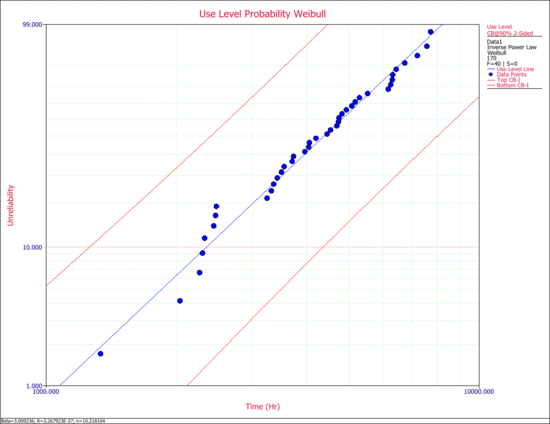
ACME manufacturing has implemented an accelerated life testing program for their new product design. A total of 40 units were tested at four different pressure levels. The operating stress level is 170 psi. The following table shows the data from the test. Determine the parameters of the inverse power law Weibull model and obtain the use level probability plot with 90% 2-sided confidence bounds on time.
| Stress Level, psi | 220 psi | 230 psi | 240 psi | 250 psi |
|---|---|---|---|---|
| 165 | 93 | 72 | 26 | |
| 177 | 106 | 73 | 44 | |
| 238 | 156 | 99 | 63 | |
| 290 | 170 | 124 | 68 | |
| Times-to-failure, hr | 320 | 185 | 134 | 69 |
| 340 | 214 | 150 | 72 | |
| 341 | 220 | 182 | 77 | |
| 380 | 236 | 186 | 96 | |
| 449 | 252 | 190 | 131 | |
| 544 | 288 | 228 | 140 |
The parameters of the IPL-Weibull model are estimated to be:
- [math]\displaystyle{ \begin{align} \beta =\ & 3.009236 \\ K=\ & 3.267923E-27 \\ n=\ & 10.218104 \end{align} }[/math]
The use level probability plot is shown next.
In ALTA, the confidence bounds on time are the Type 1 bounds (Time Bounds).
Temperature-NonThermal
12 electronic devices are put into an accelerated life test. The accelerated stresses are temperature and voltage, with use level conditions of 328K and 2V, respectively. The following table shows the data from the test:
Do the following:
1) Using the T-NT Weibull model, analyze the data and determine the MTTF and B(10) life for these devices at use level. Determine the upper and lower 90% 2-sided confidence intervals on the results.
2) Examine the effects of each stress on life.
Solution
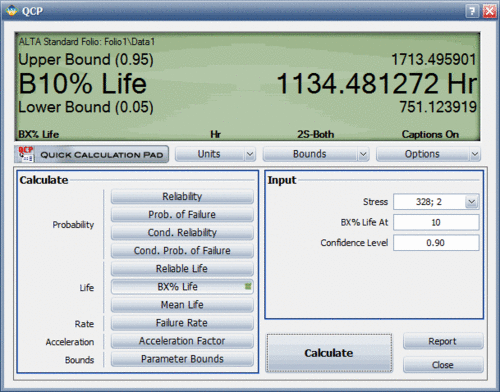
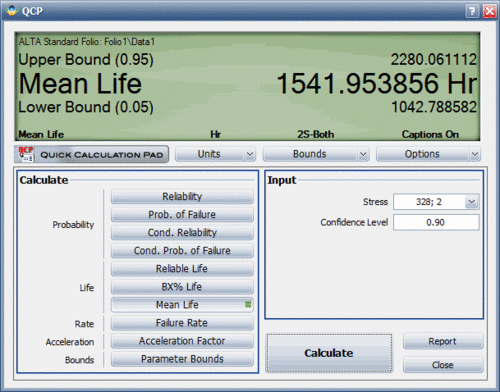
1. Analyze the data set in the ALTA standard folio and use the Quick Calculation Pad (QCP) to compute for the MTTF and [math]\displaystyle{ B(10) }[/math] life. The results are shown next.
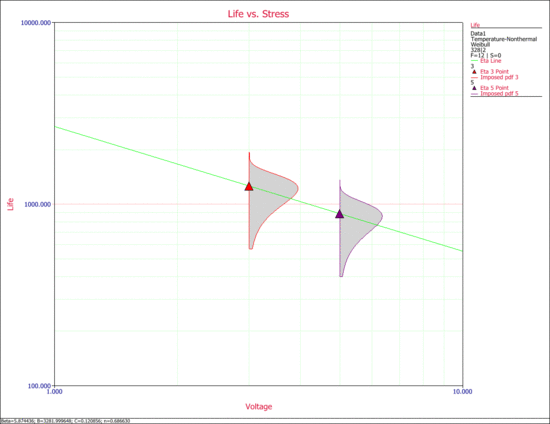
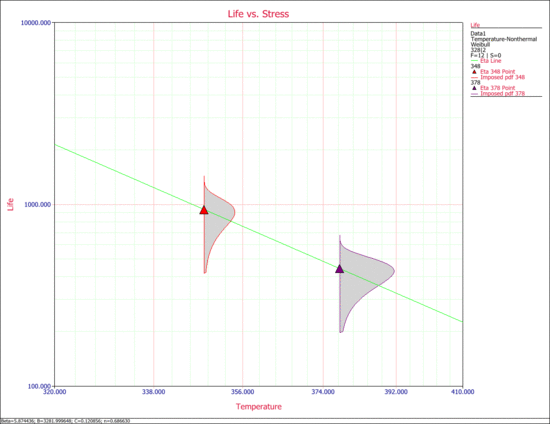
2. The next two figures examine the effects of each stress on life. Specifically, the first figure shows the Life vs. Voltage plot with the temperature held constant at 328K. The second figure shows the Life vs. Temperature plot with voltage held constant at 2V.
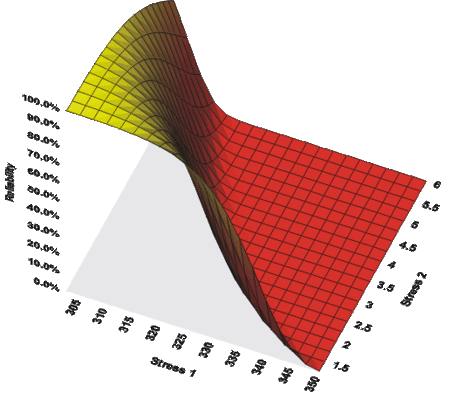
The next figure shows a 3D plot of reliability (at a constant time) versus both stresses. As you can see, the reliability declines slightly faster with the change in temperature than with the change in voltage. Note that in the following plot, Stress 1 refers to temperature and Stress 2 refers to voltage.
Cumulative Damage
- REDIRECT[1]
- REDIRECT[2]