Logistic Distribution Example
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.
This example appears in the Life Data Analysis Reference book.
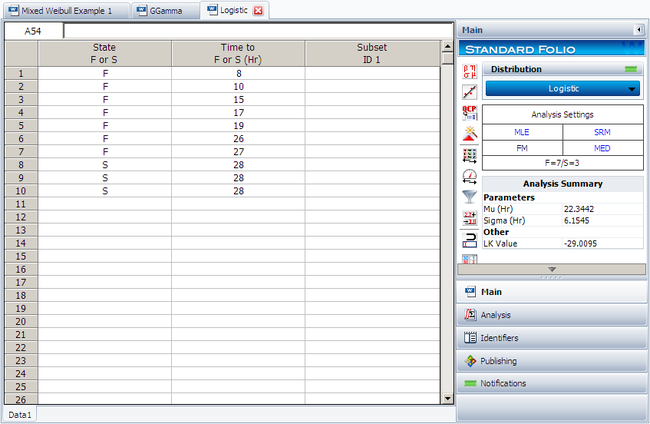
The lifetime of a mechanical valve is known to follow a logistic distribution. 10 units were tested for 28 months and the following months-to-failure data were collected.
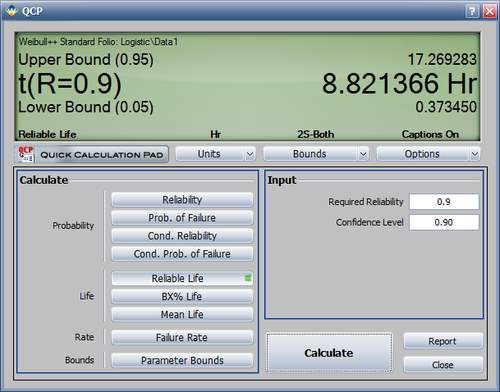
- Determine the valve's design life if specifications call for a reliability goal of 0.90.
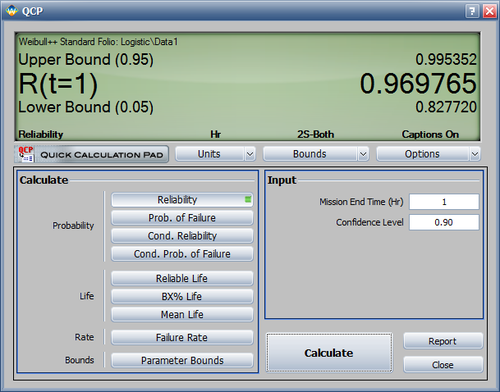
- The valve is to be used in a pumping device that requires 1 month of continuous operation. What is the probability of the pump failing due to the valve?
Enter the data set in a Weibull++ standard folio, as follows:
The computed parameters for maximum likelihood are:
- [math]\displaystyle{ \begin{align} & \widehat{\mu }= & 22.34 \\ & \hat{\sigma }= & 6.15 \end{align}\,\! }[/math]
The valve's design life, along with 90% two sided confidence bounds, can be obtained using the QCP as follows:
The probability, along with 90% two sided confidence bounds, that the pump fails due to a valve failure during the first month is obtained as follows: